区块链中的密码学（二）-RSA算法分析和实现

密码学领域中，加密算法主要分为对称加密和非对称加密，随着信息时代安全性要求越来越高，对称加密因为其易被破解的原因逐渐被舍弃。而RSA算法是目前密码学世界中比较流行的非对称加密算法，命名是根据其发明者Rives，Shamir，Adleman三人的名字缩写而来。讲到RSA就不得不提到最近"黎曼猜想被正面后RSA算法不在安全"的传言。带着这个问题，讲述完RSA的原理以后会顺带讲一下即便"黎曼猜想"被证实是否对目前一些基于RSA算法的区块链项目有影响。本文的读者默认对于素数，互质，去模的数学概念有一定的了解。

什么是非对称加密？

加密就是对一段明文信息进行特殊操作产生让人无法理解的密文，而解密就是反向前一步的操作。非对称加密就是整个加密过程中需要两个秘钥：公钥和私钥。公钥和私钥是一对，对一段明文进行公钥加密以后只有对应的私钥能解密。大致过程如下：

RSA加密

RSA加密的过程定义的公式如下：

简单说，明文的E次方对N取模的结果就是密文。相信到这里读者的疑问都是E和N到底是什么？其实这里的E和N 就是RSA加密的公钥，它们的用法我已经介绍过了，通常暴露给其他使用者的是E和N的组合。

RSA解密

RSA解密的过程定义如下：

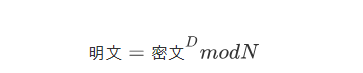
对密文取D次方，在对N取模得到的结果就是明文。这里的D和N的组合就是RSA算法的秘钥，这一步的N和加密用到的N是同一个数。

RSA 生产密钥对

通过上面的两个公式可以看到，只要知道E,D,N的值就很容易实现一次RSA加解密的过程。下面介绍一下这三个数生成的过程：

1.首先准备两个很大的质数p，q。这两个数的选择依据：如果p,q很大，算法的安全性会很高，但是相对应的计算时间会增长。一般编程语言都有对应的库用来生成这样的数据。计算p和q的乘积就得到了值N。

2.根据欧拉函数，不大于N且与N互质的整数个数有(p-1)(q-1)个。φ(n) =(q-1)*(p-1);随机选择一个整数e，要求是φ(n)>e>1，并且e与φ(n)互质，一般选择65537（如果范围允许的话）。

3.前两步生成了公钥，下面生成私钥需要的D：

D需要满足条件：

D的值就是（ φ(n)的倍数+1）/E；

到这一步就简单的实现RSA算法的加解密过程。

RSA算法安全性

相信通过上面的过程读者应该能发现，RSA运用了大量的质数运算，这也正是RSA算法的核心：当p和q是一个大素数的时候，从它们的积pq去分解因子p和q，这是一个公认的数学难题。所以当p,q的值足够大的时候，是很难根据p和q的乘积计算出p和q的值的。注意这里用的是”很难“，这也是RSA算法的缺陷，没有任何理论或概率方面的算法证明RSA算法的破解难度，所以其安全性保障也仅仅在于此，并没有如之前讲SHA256时类比宇宙中原子数量来证明碰撞的难度。RSA的安全性问题还在于这些因式分解算法随着被因式分解的数字变得越大而变得越有效率。也就是说RSA算法的安全性在一定程度上依赖于私钥的长短，而不是其本身的算法。

RSA算法和”黎曼猜想“

在文章的开头讲述了黎曼猜想，今年9月24号，英国著名数学家迈克尔·阿提亚提出了他验证黎曼猜想的思路。我们这里不打算花费大量的篇幅介绍”黎曼猜想“和证明过程。只是希望从本质上告诉读者，”黎曼猜想“的证实和RSA算法的破解是两码事。总结起来一句话就是：”黎曼猜想“被证实的结果是证明了素数的分布是有规律的，它能够帮助我们快速的定位素数的位置。然而想要破解RSA算法的本质是对两个大质数的乘积进行因式分解，这个本质上跟”黎曼猜想“的被证实没有关系。