求微分其实就是线性化，导数其实就是线性空间之间的线性变换，Jaocibian矩阵本质上就是导数。

比如，映射在处的导数就是在处的切空间到在处的切空间之间的线性映射。切空间都是矢量空间，都有基底，所以这个线性变换就是矩阵。在欧氏空间子空间的开集上，切空间就是某个，比如实轴上的切空间就是，曲面上的切空间为。这样一想，函数的导数无非就是切空间到切空间的线性变换，是一个矩阵，同构于一个实数。

因此，Jacobian矩阵实质上就是切空间之间的基底之间的线性变换，这也是为什么积分中变换坐标时前面会乘以一个Jacobian矩阵的行列式。

作者：玟清
链接：https://www.zhihu.com/question/22586361/answer/76610395
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

 
 

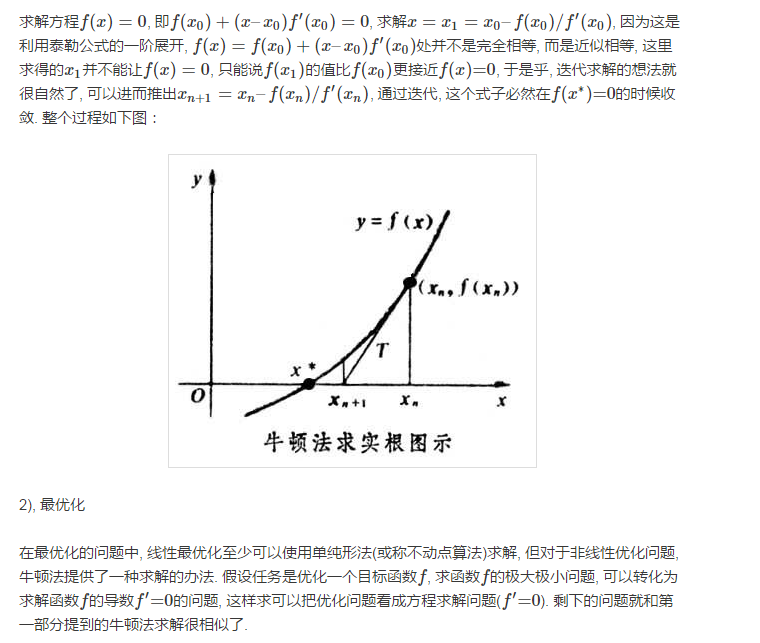
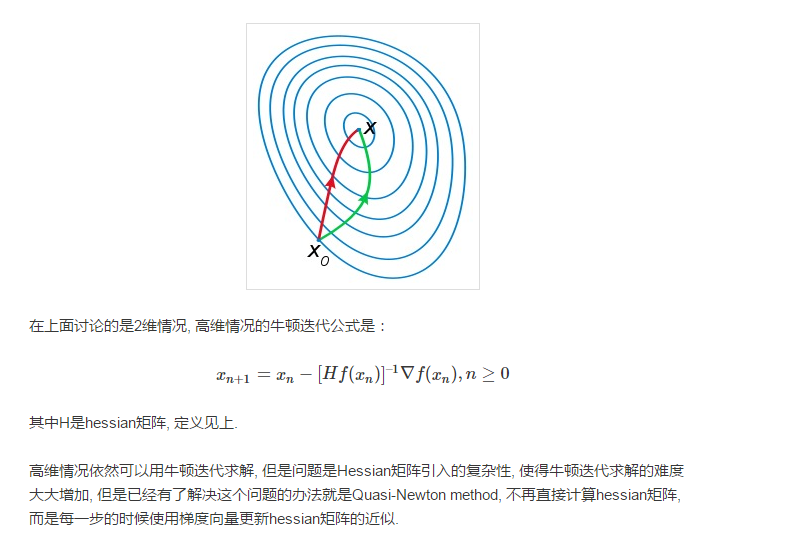
转自：http://jacoxu.com/jacobian%E7%9F%A9%E9%98%B5%E5%92%8Chessian%E7%9F%A9%E9%98%B5/

Jacobi 矩阵的更多相关文章

  1. matlab图

    .6 统计作图 4.6.1 正整数的频率表 命令 正整数的频率表 函数 tabulate 格式 table = tabulate(X) %X为正整数构成的向量,返回3列:第1列中包含X的值第2列为这些 ...

  2. GNU scientific library

    GNU scientific library 是一个强大的C,C++数学库.它涉及的面很广,并且代码效率高,接口丰富.正好最近做的一个项目中用到多元高斯分布,就找到了这个库. GNU scientif ...

  3. 机器学习数学|微积分梯度jensen不等式

    机器学习中的数学 觉得有用的话,欢迎一起讨论相互学习~Follow Me 原创文章,如需转载请保留出处 本博客为七月在线邹博老师机器学习数学课程学习笔记 索引 微积分,梯度和Jensen不等式 Tay ...

  4. Bundle Adjustment---即最小化重投影误差（高翔slam---第七讲）

    一.历史由来 Adjustment computation最早是由geodesy的人搞出来的.19世纪中期的时候,geodetics的学者就开始研究large scale triangulations ...

  5. OpenCASCADE解非线性方程组

    OpenCASCADE解非线性方程组 eryar@163.com Abstract. 在科学技术领域里常常提出求解非线性方程组的问题,例如,用非线性函数拟合实验数据问题.非线性网络问题.几何上的曲线曲 ...

  6. GSL--GNU Scientific Library 小记

    摘自http://qianjigui.iteye.com/blog/847612 GSL(GNU Scientific Library)是一个 C 写成的用于科学计算的库,下面是一些相关的包 Desi ...

  7. 理解自动梯度计算autograd

    理解自动求导 例子 def f(x): a = x * x b = x * a c = a + b return c 基于图理解 代码实现 def df(x): # forward pass a = ...

  8. 采用梯度下降优化器(Gradient Descent optimizer)结合禁忌搜索(Tabu Search)求解矩阵的全部特征值和特征向量

    [前言] 对于矩阵(Matrix)的特征值(Eigens)求解,采用数值分析(Number Analysis)的方法有一些,我熟知的是针对实对称矩阵(Real Symmetric Matrix)的特征 ...

  9. Jacobi并行拆解【补充】

    作者:桂. 时间:2018-04-24  22:04:52 链接:http://www.cnblogs.com/xingshansi/p/8934373.html 前言 本文为Jacobi并行拆解一文 ...

随机推荐

  1. 打印时报emSize必须大于0

    Value of '0' is not valid for 'emSize','emSize' should be greater than 0 and less than or equal to S ...

  2. 执行Chrome自动化时--正在受到自动软件的控制的显示屏蔽

    用selenium启动,浏览器出现‘Chrome正在受到自动软件的控制’ 屏蔽的方法: # coding:utf-8 from selenium import webdriver # 加启动配置 op ...

  3. linux Composer 安装

    Composer是一个管理PHP包依赖关系的工具.我们可以使用Composer方便地管理项目中一些第三方库和自己的库. 我们可以把Composer安装到当前目录或者特定目录甚至将它变成全局命令 *执行 ...

  4. python3 tkinter

    https://morvanzhou.github.io/tutorials/python-basic/tkinter/ 李导师推荐的.非常感谢.非常棒的视频教程!!! 只不过里面的教程视频是yout ...

  5. nginx的日志分析

    1.到NGINX把日志DOWN下来2.用命令cat xxxx.log | egrep '10/Jul/2015:01:[4-5]|2015-07-10 02:0[0-57]'>xxxx2.log ...

  6. Web安全测试指南--会话管理

    会话复杂度: 5.3.2.会话预测: 5.3.3.会话定置: 5.3.4.CSRF: 5.3.5.会话注销: 5.3.6.会话超时:

  7. IntelliJ IDEA 创建Web项目

    1:创建Project:依次点击File–new Project: 2:选择Empty Project项目,点击Next: 3:输入项目名称,选择项目路径: 4:创建Module:点击Finish,弹 ...

  8. ie6,7下的textarea的type获取

    <input type='button' value="按钮" class='gys'> <textarea class='gys gystextarea'> ...

  9. GameObject数组

    一.声明 GameObject[] rock = ]; 二.遍历 可以先声明一个GameObject的数组GameObject[], 然后把需要遍历的对象放进去,然后可以用下面两种方式遍历:1.for ...

  10. 《opencv学习》 之 特征检测与匹配

    这几天学习SURF特征检测,直接看的视频和书本有点吃不消,现在是基本看懂了,如果写博客记录没有必要,因为网上都差不多,笔记都在书上了,以下是个人认为比较浅显易懂的文章,当然海有很多好文章我没看到. 看 ...