UVA 11881 - Internal Rate of Return - [二分]

依然是来自2017/9/17的周赛水题……

题目链接：https://cn.vjudge.net/problem/UVA-11881

题解：

观察这个函数：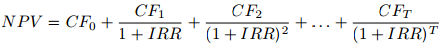

由于CF[i]固定值，因此NPV(IRR)这个函数，是连续单减函数，其值域区间为从+∞到CF[0]；

那么显然的，NPV(IRR) = 0方程的解必然有且仅有一个，所以题目中“Too many”和“No”的输出纯粹掩人耳目，实际上是不会有test case输出这两个的；

那么要得到IRR的一定精确度的数值，显然二分法求即可。

AC代码：

 #include<cstdio>
 #include<cmath>
 int t,cf[];
 double l,r,mid;
 double ans;
 double calc(double IRR)
 {
     double ans=cf[]*1.0;
     for(int i=;i<=t;i++) ans+=(cf[i]*1.0)/pow(+IRR,i);
     return ans;
 }
 int main()
 {
     while(scanf("%d",&t) && t>)
     {
         for(int i=;i<=t;i++) scanf("%d",&cf[i]);
         l=-1.0, r=1e8;
         while(r-l>1e-)
         {
             mid=(l+r)/;
             double tmp=calc(mid);
             if(tmp>=) l=mid;
             else r=mid;
         }
         printf("%.2lf\n",l);
     }
 }