【CSP-S膜你考】最近公共祖先 （数学）

Problem A. 最近公共祖先 (commonants.c/cpp/pas)

注意

Input file: commonants.in

Output file: commonants.out

Time Limit : 0.5 seconds

Memory Limit: 512 megabytes

题面

最近公共祖先\(\text{(Lowest Common Ancestor,LCA)}\)是指在一个树中同时拥有给定的两个点作为后

代的最深的节点。

为了学习最近公共祖先，你得到了一个层数为\(n+1\)的满二叉树，其中根节点的深度为\(0\)，其他节点的深度为父节点的深度\(+1\)。你需要求出二叉树上所有点对 \(\texttt{(i,j)}\),（\(i\),\(j\)可以相等，也可以\(i > j\)）的最近公共祖先的深度之和对\(10^9+7\)取模后的结果。

输入格式

一行一个整数\(n\)。

输出格式

一行一个整数表示所有点对 \(\texttt{(i,j)}\),（\(i\),\(j\)可以相等，也可以\(i > j\)）的最近公共祖先的深度之和对\(10^9+7\)取模后的结果。

样例

\(\texttt{input\#1}\)

2

\(\texttt{input\#2}\)

19260817

\(\texttt{output\#1}\)

22

\(\texttt{output\#2}\)

108973412

数据范围与提示

样例\(1\)解释：

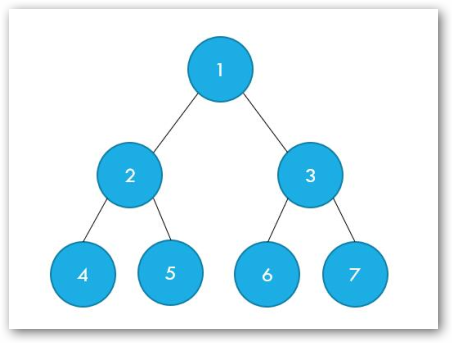
树一共有\(7\)个节点（一个根节点和两个子节点），其中 \(\texttt{(4,4),(5,5),(6,6),(7,7)}\) 共\(4\)对的最近公共祖先深度为\(2\)，\(\texttt{(4,2),(2,4),(5,2),(2,5),(5,4),(4,5),(2,2),(6,3),(3,6),(3,7),(7,3),(6,7),}\)\(\texttt{(7,6),(3,3)}\)共\(14\)对最近公共祖先深度是\(1\)，其他的点对最近公共祖先深度为\(0\)，所以答案为\(22\)。

对于\(20%\)的数据，\(n \le 10\)。

对于\(50%\)的数据，\(n \le 10^6\) 。

对于\(100%\)的数据，\(1 \le n \le 10^9\) 。

---

题解

对于一颗有\(n\)层的满二叉树很显然符合以下几点

1.第\(i\)层的点的个数为\(2^i\)。

2.以第\(i\)层的点为根节点的子树大小为\(2^{n-i+1}-1\)。

3.以第\(i\)层的点为\(\text{LCA}\)的点对个数为\(2^{2n-i+1}-2^i\)



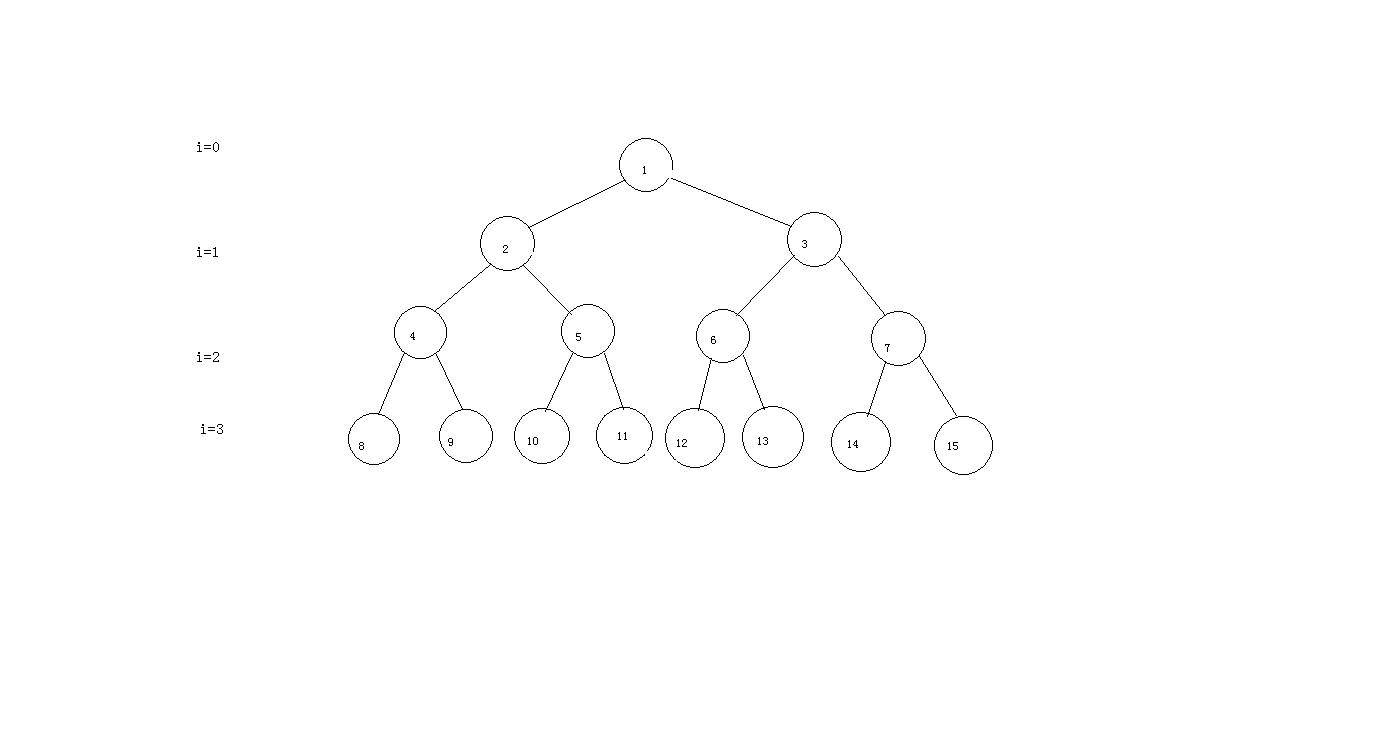
观察上面的图（好丑）,很明显\(1,2\)都是对的。

对于一颗以第\(i\)层的节点为根的子树：

①它的左子树与右子树上的点的\(\text{LCA}\)都为根节点。所以点对个数为

\[\LARGE\frac{2^{n-i+1}-2}{2} \times \frac{2^{n-i+1}-2}{2}
\]

\[\LARGE= (2^{n-i}-1) \times (2^{n-i}-1)
\]

\[\LARGE= 2^{2n-2i}-2^{n-i+1}+1
\]

②这棵子树的左子树与根节点的\(\text{LCA}\)都为根节点。右子树也是。所以有\(2^{n-i+1}-2\)对点。

③根节点与根节点的\(\text{LCA}\)也是根节点，点对个数为1。

点对\(\texttt{(u,v)}\)与点对\(\texttt{(v,u)}\)在\(u \neq v\)时是两个不同的点对。

所以将上述①②相加乘二再加③就是以子树根节点为\(\text{LCA}\)的点对的数量为：

\[\LARGE 2^{2n-2i+1}-1
\]

因为第\(i\)层的点的个数为\(2^i\)。所以以第\(i\)层的点为\(\text{LCA}\)的点对个数为：

\[\LARGE 2^{2n-i+1}-2^i
\]

因为一共有\(n+1\)层，从\(0-n\)层，所以答案为：

\[\LARGE \sum_{i=0}^{n} (2^{2n-i+1}-2^i) \times i
\]

\[\LARGE =\sum_{i=0}^{n} i \times 2^{2n-i+1}-i \times 2^i
\]

但这样复杂度为\(\Theta (nlog_n)\)过不了。。将上面的式子展开：

\[\LARGE \sum_{i=0}^{n} i \times 2^{2n-i+1} - \sum_{i=0}^{n} i \times 2^i
\]

\[\LARGE T_n=\sum_{i=0}^{n} i \times 2^{2n-i+1}
\]

\[\LARGE =2^{2n} + 2 \times 2^{2n-1} + 3 \times 2^{2n-2}+...+n \times 2^{n+1}
\]

\[\LARGE 2T_n=2^{2n+1} + 2 \times 2^{2n} + 3 \times 2^{2n-1}+...+n \times 2^{n+2}
\]

\[\Large 2T_n-T_n=2^{2n+1} + 2^{2n} + 2^{2n-1}+...+2^{n+2} - n \times 2^{n+1}
\]

\[\LARGE T_n=2^{2n+1} + 2^{2n} + 2^{2n-1}+...+2^{n+2} - n \times 2^{n+1}
\]

很明显前\(n\)项为等比数列，利用等比数列求和公式可以很快求出。

\[\LARGE T_n=\sum_{i=0}^{n} i \times 2^i
\]

\[\LARGE =2 + 2 \times 2^2 + 3 \times 2^3 +...+ n \times 2^n
\]

\[\LARGE 2T_n=2^2 + 2 \times 2^3 + 3 \times 2^4 + ... + n \times 2^{n+1}
\]

\[\LARGE T_n-2T_n=2 + 2^2 + 2^3 +...+2^n- n \times 2^{n+1}
\]

很明显也是等比数列。将这两个相加就是答案了。

快速幂是\(log\)。所以复杂度是\(\Theta(log_n)\)

---

\(Code\)

#include<bits/stdc++.h>
typedef long long ll;
ll n;
const ll mod=1000000007;

inline void read(ll &T) {
    ll x=0;bool f=0;char c=getchar();
    while(c<'0'||c>'9'){if(c=='-')f=!f;c=getchar();}
    while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
    T=f?-x:x;
}

inline ll qpow(ll a,ll b) {
    ll ans=1,base=a;
    while(b) {
        if(b&1) ans=(ans*base)%mod;
        base=(base*base)%mod;
        b>>=1;
    }
    return ans%mod;
}

int main() {
    read(n);
    ll qwq=(((2*qpow(2,2*n+1))%mod-qpow(2,n+2)+5*mod)%mod-n*qpow(2,n+1)+5*mod)%mod;
    ll qaq=((((2*qpow(2,n))%mod)-2+5*mod)%mod-n*qpow(2,n+1)+5*mod)%mod;
    //std::cout<<qwq<<'\n'<<qaq<<'\n';
    std::cout<<(qwq+qaq+5*mod)%mod;//加上一个模数再取模是为了处理负数的情况
    return 0;
}