JDOJ 1927 求逆序对

洛谷 P1908 逆序对

洛谷传送门

JDOJ 1927: 求逆序对

JDOJ传送门

题目描述

猫猫TOM和小老鼠JERRY最近又较量上了，但是毕竟都是成年人，他们已经不喜欢再玩那种你追我赶的游戏，现在他们喜欢玩统计。最近，TOM老猫查阅到一个人类称之为“逆序对”的东西，这东西是这样定义的：对于给定的一段正整数序列，逆序对就是序列中ai>aj且i<j的有序对。知道这概念后，他们就比赛谁先算出给定的一段正整数序列中逆序对的数目。

Update:数据已加强。

输入格式

第一行，一个数n，表示序列中有n个数。

第二行n个数，表示给定的序列。序列中每个数字不超过10^9109

输出格式

给定序列中逆序对的数目。

输入输出样例

输入 #1复制

输出 #1复制

说明/提示

对于25%的数据，n \leq 2500n≤2500

对于50%的数据，n \leq 4 \times 10^4n≤4×104。

对于所有数据，n \leq 5 \times 10^5n≤5×105

请使用较快的输入输出

应该不会n方过50万吧 by chen_zhe

题目略有不同，不影响双AC。

题解：

求逆序对我们一般使用归并排序，所谓归并排序，让我用一张图简单解释一下：

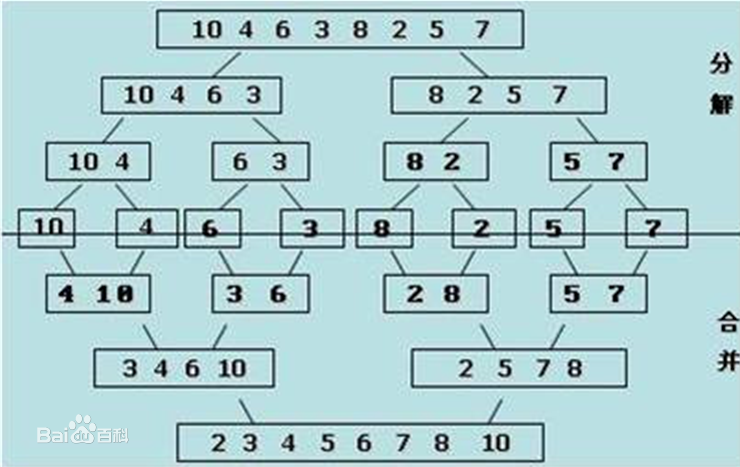
通过从百度百科上扒下来的这个图，我们可以发现归并排序其实是分治算法的一个简单应用。

归并归并，顾名思义，先分再并，针对一个无序序列，通过把元素分解之后交换顺序，最后合并出一个有序序列。

针对于求逆序对个数的问题，我们很容易得出，逆序对的个数就是归并排序过程中交换的次数。

请好好理解。

然后我们来看一看用树状数组如何实现求逆序对个数的题目。

方法1，传统方法，向下查询，向上修改。

这个方法需要逆向枚举每一个数，先查询一下已经插入的树状数组中比其小的元素个数，再累加ans。

然后先累加，再把它放到树状数组里。

方法2，向上查询，向下修改。

其实就是反过来。

正向枚举，先向上查询，根据树状数组的结构可以得出，查询到的结果就是已经插入到树状数组的比当前值大的元素的个数，累加ans即可。

但是在这里，为了满足洛谷的坑比需求，我采用了结构体排序加树状数组的一个方法。

详见代码。

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
int c[500010],rk[500010],n;
long long ans;
struct point
{
    int num,val;
}a[500010];
inline bool cmp(point q,point w)
{
    if(q.val==w.val)
        return q.num<w.num;
    return q.val<w.val;
}
inline void fix(int p,int d)
{
    for(;p<=n;p+=p&-p)
        c[p]+=d;
}
inline int getsum(int x)
{
    int sum=0;
    for(;x;x-=x&-x)
        sum+=c[x];
    return sum;
}
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        scanf("%d",&a[i].val),a[i].num=i;
    sort(a+1,a+1+n,cmp);
    for(int i=1;i<=n;i++)
        rk[a[i].num]=i;
    for(int i=1;i<=n;i++)
    {
        fix(rk[i],1);
        ans+=i-getsum(rk[i]);
    }
    printf("%lld",ans);
    return 0;
}