查找->静态查找表->次优查找(静态树表)

文字描算

　　之前分析顺序查找和折半查找的算法性能都是在“等概率”的前提下进行的，但是如果有序表中各记录的查找概率不等呢？换句话说，概率不等的情况下，描述查找过程的判定树为何类二叉树，其查找性能最佳？

　　如果只考虑查找成功的情况，则使查找性能达最佳的判定树是其带权内路径长度之和PH值取最小的二叉树。

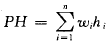
　　其中n为二叉树上结点的个数(即有序表的长度)；hi为第i个结点在二叉树上的层次数；结点的权w_i=cpi(i=1,2,…,n)，其中pi为结点的查找概率，c为某个常量。称PH值取最小的二叉树为静态最优查找树。由于构造静态最优查找树代价较高，在此介绍一种构造近似最优查找树的有效算法。该算法的过程描述如下：

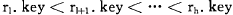　　已知一个按关键字有序的记录序列,其中, 与每个记录相应的权值为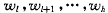

　　首先在记录序列中取第i(l<=i && i<=h)个记录构造根结点，使得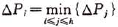取最小值，然后分别对子序列和构造两棵次优查找树，并分别设为根结点的左子树和右子树。

示意图

算法分析

　　从次优查找树的结构特定可知，其查找过程类似于折半查找。查找过程和二叉排序树算法类型，待二叉排序树会讲。由于查找过程是走了一条从根到待查记录所在节点(或叶子结点)的一条路径，进行过比较的关键字个数不超过树的深度，因此，次优查找树的平均查找长度和logn成正比。可见，在记录的查找概率不等时，可用次优查找树表示静态查找表，故又称为静态树表。

另外，大量实验表明，次优查找树和最优查找树的查找性能之差仅仅为1%-2%，很少查过3%，而且构造次优查找树的算法的时间复杂度为nlogn。

代码实现

 #include <stdio.h>
 #include <stdlib.h>
 #include <string.h>

 #define DEBUG
 #define EQ(a, b) ((a)==(b))
 #define LT(a, b) ((a)< (b))
 #define LQ(a, b) ((a)<=(b))
 #define MAX_SIZE 50

 typedef char KeyType;
 //数据元素类型
 typedef struct{
     //关键字
     KeyType key;
     //权值
     int weight;
 }ElemType;
 //静态查找表
 typedef struct{
     //数据元素存储空间基址,0号单元留空
     ElemType *elem;
     //表长度
     int length;
 }SSTable;
 //二叉链表, 次优查找树采用二叉链表的存储结构
 typedef struct{
     ElemType data;
     struct BiTNode *lchild;
     struct BiTNode *rchild;
 }BiTNode, *BiTree;

 //由有序表R[low,...,high]及累计权值表sw(其中sw[0]==0)递归构造次优查找树T
 BiTNode* SecondOptimal(ElemType R[], int sw[], int low, int high)
 {
     int i = low, j = ;
     int min = abs(sw[high]-sw[low]);
     int dw = sw[high]+sw[low-];
     //选择最小的<>Pi值
     for(j=low+; j<=high; ++j){
         if(abs(dw-sw[j]-sw[j-])<min){
             i = j;
             min = abs(dw-sw[j]-sw[j-]);
         }
     }
 #ifdef DEBUG
     printf("i=%d, low=%d, high=%d\n", i, low, high);
 #endif
     //生成结点
     BiTNode* T = (BiTNode*)malloc(sizeof(BiTNode));
     T->data = R[i];
     T->lchild = T->rchild = NULL;
     if(i==low){
         //左子树空
         T->lchild = NULL;
     }else{
         //构造左子树
         T->lchild = SecondOptimal(R, sw, low, i-);
     }
     if(i==high){
         //右子树空
         T->rchild = NULL;
     }else{
         //构造右子树
         T->rchild = SecondOptimal(R, sw, i+, high);
     }
     return T;
 }

 //按照由有序表ST中各数据元素的weight域求累计权值表sw
 void FindSW(int sw[], SSTable ST)
 {
     int i = ;
     sw[] = ;
     for(i=; i<=ST.length; i++){
         sw[i] = sw[i-]+ST.elem[i].weight;
     }
 #ifdef DEBUG
     printf("SW  : ");
     for(i=; i<=ST.length; i++){
         printf("[%d]=%-3d  ", i, sw[i]);
     }
     printf("\n");
 #endif
     return ;
 }

 //由有序表ST构造一棵次优查找树. ST的数据元素含有权域weight
 BiTree CreateSOSTree(SSTable ST)
 {
     if(ST.length == )
         return NULL;
     else{
         int sw[MAX_SIZE+] = {};
         //按照由有序表ST中各数据元素的weight域求累计权值表sw
         FindSW(sw, ST);
         //由有序表ST.elem[low,...,high]及累计权值表sw(其中sw[0]==0)递归构造次优查找树并返回
         return (BiTree)SecondOptimal(ST.elem, sw, , ST.length);
     }
 }

 //顺序打印有序表ST中的数据元素。
 void print(SSTable SS){
     printf("data: ");
     int i = ;
     for(i=; i<=SS.length; i++){
         printf("[%d]=%c,%d  ", i, SS.elem[i].key, SS.elem[i].weight);
     }
     printf("\n");
 }

 int PreOrderTraverse(BiTree T);    //先序遍历
 int InOrderTraverse(BiTree T);    //中序遍历
 int PostOrderTraverse(BiTree T);//后序遍历

 int main(int argc, char *argv[])
 {

     KeyType key;
     int weight;
     int i = ;
     char tmp[] = {};
 #ifdef DEBUG
     ElemType arr[MAX_SIZE+] = {{'',},{'A',}, {'B',}, {'C',}, {'D',}, {'E',},{'F',},{'G',},{'H',},{'I',},};
     i = ;
 #else
     ElemType arr[MAX_SIZE+];
     while(){
         printf("输入 关键字,权值('0,0'是结束):");
         memset(tmp, , sizeof(tmp));
         scanf("%s", tmp);
         sscanf(tmp, "%c,%d", &key, &weight);
         if(key == '' && weight ==){
             break;
         }else{
             arr[i].key = key;
             arr[i].weight = weight;
             i+=;
         }
     }
 #endif
     SSTable SS;
     SS.elem = arr;
     SS.length = i-;
 #ifdef DEBUG
     print(SS);
 #endif
     BiTree T = CreateSOSTree(SS);
     printf("先序遍历:");
     PreOrderTraverse(T);
     printf("\n");

     printf("中序遍历:");
     InOrderTraverse(T);
     printf("\n");

     printf("后序遍历:");
     PostOrderTraverse(T);
     printf("\n");
     return ;
 }

 int PreOrderTraverse(BiTree T){
     if(T){
         printf("%c,%d  ", ((BiTNode*)T)->data.key, ((BiTNode*)T)->data.weight);
         PreOrderTraverse((BiTree)T->lchild);
         PreOrderTraverse((BiTree)T->rchild);
     }
     return ;
 }

 int InOrderTraverse(BiTree T){
     if(T){
         InOrderTraverse((BiTree)T->lchild);
         printf("%c,%d  ", ((BiTNode*)T)->data.key, ((BiTNode*)T)->data.weight);
         InOrderTraverse((BiTree)T->rchild);
     }
     return ;
 }

 int PostOrderTraverse(BiTree T){
     if(T){
         PostOrderTraverse((BiTree)T->lchild);
         PostOrderTraverse((BiTree)T->rchild);
         printf("%c,%d  ", ((BiTNode*)T)->data.key, ((BiTNode*)T)->data.weight);
     }
     return ;
 }

次优查找(静态树表)

运行