bzoj 3522 / 4543 [POI 2014] Hotel - 动态规划 - 长链剖分

题目传送门

• bzoj 3522
  • 需要root权限的传送点
• bzoj 4543
  • 快速的传送点
  • 慢速的传送点

题目大意

　　给定一棵树，问有多少个无序三元组$(x, y, z)$使得这三个不同点在树上两两距离相等。

　　考虑这三个点构成的虚树。选取一个"舒适"的计数对象。

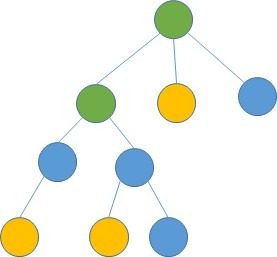
　　其中黄色的点是关键点，绿色的点是虚树上的虚点。

　　在树形动态规划的时候通常考虑一个点子树内的情况会比较简单。因此考虑将计数对象设为虚树上最浅的一个点。

性质1 最近公共祖先深度较深的两点到它们的最近公共祖先的距离相等。

　　证明 设这两点为$A, B$，第三点为$C$。当三个点的最近公共祖先相同时显然。否则第三点到这两点距离不相等。

　　当三个点的最近公共祖先不相同时。设$A$和$B$两点的最近公共祖先为$D$。

　　因为三个点公共祖先不同所以$C$在$D$的子树外。　　

　　此时虚树上有5个点，因为$A$和$C$、$B$和$C$的最近公共祖先是相同点，设它为$E$。

　　那么有$dis(A, D) + dis(D, E) + dis(E, C) = dis(B, D) + dis(D, E) + dis(E, C)$

　　所以$dis(A, D) = dis(B, D)$。

　　用$f[i][j]$表示在$i$的子树中，到点$i$距离为$j$的点的个数。

　　如果点$x, y$的LCA的深度为$d$，且它们到它们的LCA的距离相等，$g[i][j]$表示在$i$的子树中，有多少个点对$(x, y)$使得它们的LCA到点$i$的距离为$d - j$。

　　为了避免算重，应当边在合并子树的信息的时候边计算答案。

　　除了$f[i][0]$初始为1，其他初始为0。

　　设$i$的某个子节点为$k$。那么转移有（顺序不是这样的）：

　　$f[i][j] = f[i][j] + f[k][j - 1]$

　　$g[i][j] = g[i][j] + g[k][j + 1]$

　　$g[i][j] = g[i][j] + f[i][j] * f[k][j - 1]$ （当前点是较深的LCA）

　　$result = result + f[i][j] * g[k][j - 1] + g[i][j] * f[k][j + 1]$

　　于是状态$O(n^{2})$，时间复杂度也是满满的$O(n^{2})$。成功爆炸。

　　注意到前两个转移只是挪一挪指针，而初始的时候$f, g$几乎可以看成没有值。因此这一部分考虑直接通过指针赋值来实现$O(1)$转移。

　　问题是，这个只能做一次。那就选择深度最深的子树进行转移。

性质2 该种做法时间复杂度$O(n)$。

　　证明 对树进行长链剖分。当且仅当一条边是虚边的时候需要暴力进行转移，时间复杂度是这棵子树的深度。

　　这个深度的意义可以看成虚边深的一端连接的长链的长度。因为长链一直连向叶子结点，中间不会有其他虚边。

　　又因为长链覆盖整棵树。因此时间复杂度$O(n)$。

　　然后开一个内存池动态分配空间。（其实直接new也是可以的，只是慢一点）。　　

Code

 /**
  * bzoj
  * Problem#3522        & 4543
  * Accepted            & Accepted
  * Time: 44ms        & 768ms
  * Memory: 19652k    & 21900k
  */
 #include <iostream>
 #include <cassert>
 #include <cstdlib>
 #include <cstdio>
 #include <vector>
 #ifndef WIN32
 #define Auto "%lld"
 #else
 #define Auto "%I64d"
 #endif
 using namespace std;
 typedef bool boolean;
 #define ll long long

 const int N = ;

 ll pool[ * N];
 ll* top = pool;

 ll* alloc(int len) {
     ll* rt = top;
     top += len;
     return rt;
 }

 int n;
 ll res = ;
 vector<int> mg[N];
 int ml[N], longs[N];
 ll *f[N], *g[N];

 inline void init() {
     scanf("%d", &n);
     for (int i = , u, v; i < n; i++) {
         scanf("%d%d", &u, &v);
         mg[u].push_back(v);
         mg[v].push_back(u);
     }
 }

 void dfs1(int p, int fa) {
     ml[p] = ;
     int maxl = -, id = -;
     for (int i = ; i < (signed) mg[p].size(); i++) {
         int e = mg[p][i];
         if (e == fa)    continue;
         dfs1(e, p);
         ml[p] = max(ml[p], ml[e] + );
         if (ml[e] > maxl)
             maxl = ml[e], id = e;
     }
     longs[p] = id;
 }

 void dfs2(int p, int fa, int& maxlen, int blank) {
     maxlen = max(maxlen, ml[p]);
     if (longs[p] != -) {
         dfs2(longs[p], p, maxlen, blank + );
         res += g[longs[p]][];
         f[p] = f[longs[p]] - , f[p][] = ;
         g[p] = g[longs[p]] + ;
     } else {
         f[p] = alloc(maxlen +  + blank) + blank;
         g[p] = alloc(maxlen +  + blank);
         f[p][] = ;
     }

     for (int i = ; i < (signed) mg[p].size(); i++) {
         int e = mg[p][i], mxlen = ;
         if (e == fa || e == longs[p])    continue;
         dfs2(e, p, mxlen, );
 //        assert(f[p] + ml[e] + 1 < org[p] + siz[p]);
         for (int j = ; j < ml[e]; j++)
             res += f[p][j] * g[e][j + ];
         for (int j = ; j <= ml[e] + ; j++)
             res += g[p][j] * f[e][j - ];
         for (int j = ; j <= ml[e] + ; j++)
             g[p][j] += f[p][j] * f[e][j - ];
         for (int j = ; j <= ml[e]; j++)
             f[p][j + ] += f[e][j];
         for (int j = ; j <= ml[e]; j++)
             g[p][j - ] += g[e][j];
     }
 }

 inline void solve() {
     int mxlen = ;
     dfs1(, );
     dfs2(, , mxlen, );
     printf(Auto, res);
 }

 int main() {
     init();
     solve();
     return ;
 }