01_设计一个有getMin功能的栈

01_设计一个有getMin功能的栈

【题目】

实现一个特殊的栈，在实现栈的基本功能的基础上，再实现返回栈中最小元素的操作。

【要求】

1. pop、push、getMin操作的时间复杂度都是O(1)
2. 设计的栈类型可以使用现成的栈结构

方法一：

【思路】我们使用两个栈，一个栈用来保存当前栈中的元素，其功能和一个正常的栈没有区别，这个栈记为 stackData；另一个栈用于保存每一步的最小值，这个栈记为 stackMin。具 体的实现方式有两种

(1)压入数据规则

假设当前数据为newNum，先将其压入stackData。然后判断 stackMin 是否为空：

• 如果为空，则 newNum 也压入 stackMin。
• 如果不为空，则比较 newNum 和 stackMin 的栈顶元素中哪一个更小;
  • 如果 newNum 更小或两者相等，则 newNum 也压入 stackMin；
  • 如果 stackMin 中栈顶元素小，则 stackMin 不压入任何内容。

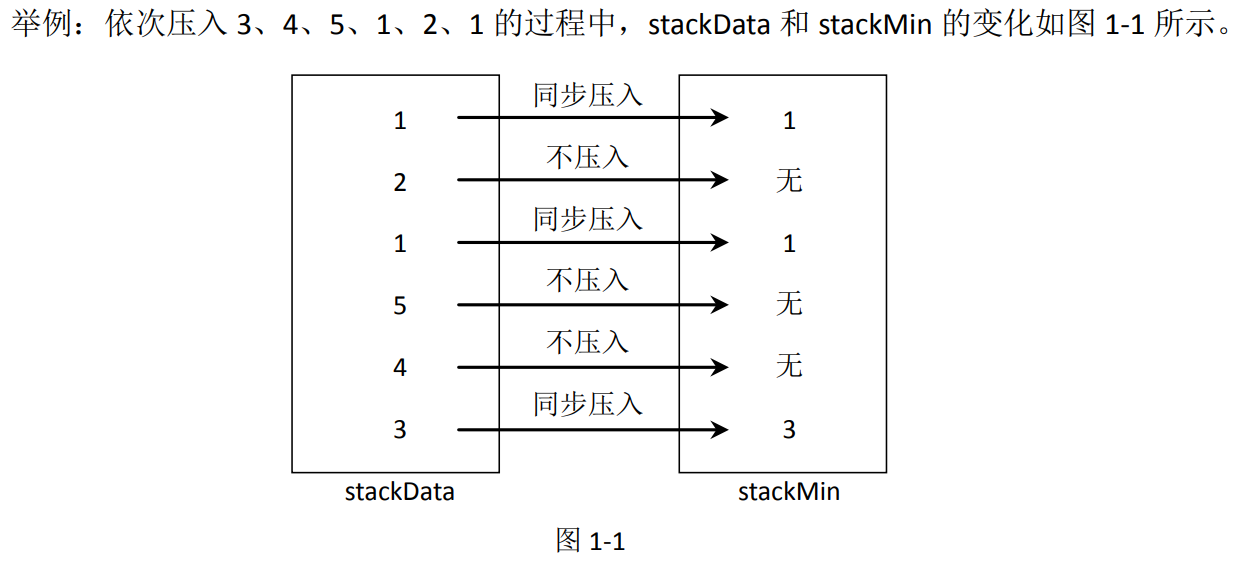
（2）弹出数据规则 先在 stackData 中弹出栈顶元素，记为 value。然后比较当前 stackMin 的栈顶元素和 value 哪一个更小。 通过上文提到的压入规则可知，stackMin 中存在的元素是从栈底到栈顶逐渐变小的， stackMin 栈顶的元素既是 stackMin 栈的最小值，也是当前 stackData 栈的最小值。所以不会出现 value 比 stackMin 的栈顶元素更小的情况，value 只可能大于或等于 stackMin 的栈顶元素。 当 value 等于 stackMin 的栈顶元素时，stackMin 弹出栈顶元素；当 value 大于 stackMin 的栈 顶元素时，stackMin 不弹出栈顶元素，返回 value。 很明显可以看出，压入与弹出规则是对应的。

（3）查询当前栈中的最小值操作 由上文的压入数据规则和弹出数据规则可知，stackMin 始终记录着 stackData 中的最小值。 所以，stackMin 的栈顶元素始终是当前 stackData 中的最小值。

方案一的代码实现如 MyStack1 类所示：

import com.sun.org.apache.bcel.internal.generic.IF_ACMPEQ;

import java.util.Stack;

/**
 * 1、设计一个有getMin功能的栈
 *
 * 【题目】
 *
 * 实现一个特殊的栈，在实现栈的基本功能的基础上，再实现返回栈中最小元素的操作。
 *
 * 【要求】
 *
 * 1. pop、push、getMin操作的时间复杂度都是O(1)
 * 2. 设计的栈类型可以使用线成的栈结构
 */
public class MyStack1 {
    private Stack<Integer> stackData;
    private Stack<Integer> stackMin;

    public MyStack1() {
        this.stackData = new Stack<Integer>();
        this.stackMin = new Stack<Integer>();
    }

    //压栈
    public void push(int newNum) {
        // 判断存放最小值的栈是否为空，不为空直接入栈
        if (this.stackMin.isEmpty()) {
            this.stackMin.push(newNum);
        } else if (newNum <= this.getMin()) {
            this.stackMin.push(newNum);
        }
        this.stackData.push(newNum);
    }

    public int pop() {
        if (this.stackData.isEmpty()) {
            throw new RuntimeException("栈中元素为空！");
        }
        int value = this.stackData.pop();
        if (value == this.getMin()) {
            this.stackMin.pop();
        }
        return value;
    }

    private int getMin() {
        if (this.stackMin.isEmpty()) {
            throw new RuntimeException("栈中元素为空！");
        }
        // Java利用Stack类的peek()函数获取堆栈中的顶部元素
        return this.stackMin.peek();
    }
}

本题对应于leetcode

对应于leetcode上的实现方式如下：

class MinStack {

    Stack<Integer> stackData;
    Stack<Integer> stackMin;

    public MinStack() {
        this.stackData = new Stack();
        this.stackMin = new  Stack();
    }
    // 将val元素压入栈
    public void push(int val) {
        // 1.1 存放最小值的栈stackMin是否为空，若为空则将当前元素压入栈
        // 1.2 判断当前stackMin栈的栈顶元素与val大小，若当前val更小，则压入栈
        if(stackMin.isEmpty() || stackMin.peek() >= val) {
            stackMin.push(val);
        }
        stackData.push(val);
    }

    //删除堆栈栈顶元素
    public void pop() {
        // 这里stackMin出栈的情况主要是当stackData出栈的元素是栈最小值元素的情形
        if (stackData.pop().equals(stackMin.peek())) {
          this.stackMin.pop();
        }
    }
    //获取堆栈顶部的元素
    public int top() {
        return this.stackData.peek();
    }

    // 获取堆栈的中的最小元素
    public int getMin() {
        return stackMin.peek();
    }
}

方法二：

（1）压入数据规则

假设当前数据为newNum，先将其压入stackData。然后判断stackMin是否为空。如果为空，则newNum也压入stackMin；如果不为空，则比较newNum和stackMin的栈顶元素中哪一个更小。

如果newNum更小或者两者相等，则newNum也压入stackMin；如果stackMin中栈顶元素小，则把stackMin的栈顶元素重复压入stackMin，即在栈顶元素上再压入一个栈顶元素。

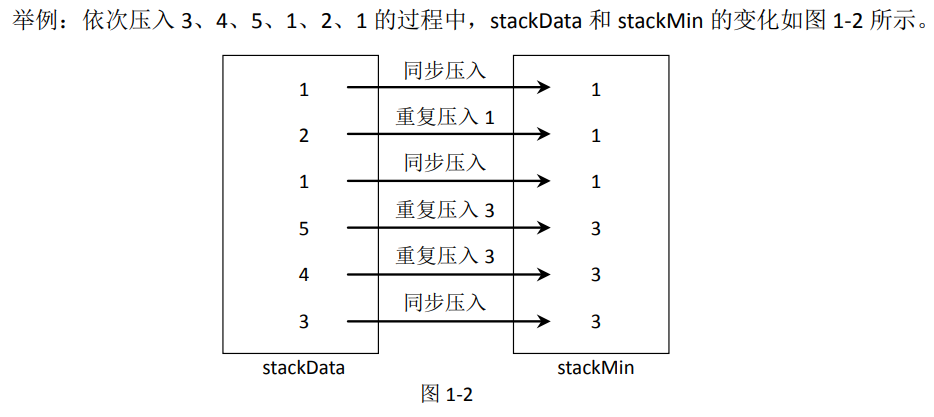
（2）弹出数据规则

在stackData中弹出数据，弹出的数据即为value；弹出stackMin中的栈顶，返回value。

（3）查询当前栈中的最小值操作

由于上文的压入数据规则和弹出数据规则可知，stackMin始终记录着stackData中的最小值，所以stackMin的栈顶元素始终是当前stackData中的最小值。

import java.util.Stack;

/**
 * 1、设计一个有getMin功能的栈
 *
 * 【题目】
 *
 * 实现一个特殊的栈，在实现栈的基本功能的基础上，再实现返回栈中最小元素的操作。
 *
 * 【要求】
 *
 * 1. pop、push、getMin操作的时间复杂度都是O(1)
 * 2. 设计的栈类型可以使用线成的栈结构
 */
// 方法二
public class MyStack2 {
    //普通栈保存栈中的元素，功能和一个正常的栈没有区别
    private Stack<Integer> stackData;
    //保存每一步的最小值
    private Stack<Integer> stackMin;

    public MyStack2() {
        this.stackData = new Stack<Integer>();
        this.stackMin = new Stack<Integer>();
    }

    //压栈
    public void push(int newNum) {
        // 判断存放最小值的栈是否为空，不为空直接入栈
        if (this.stackMin.isEmpty()) {
            this.stackMin.push(newNum);
        } else if (newNum < this.getMin()) {  // 判断当前元素是否要入stackMin中,和stackMin的栈顶元素进行比较,若发现newNum更小则入栈,反之不入stackMin栈
            this.stackMin.push(newNum);
        } else {
            this.stackMin.push(this.stackMin.peek());
        }
        // 所有的新元素都会入StackData栈
        this.stackData.push(newNum);
    }
    //出栈
    public int pop() {
        // 判断栈中元素是否为空
        if (this.stackData.isEmpty()) {
            throw new RuntimeException("栈中元素为空！");
        }
        this.stackMin.pop();
        return this.stackData.pop();
    }

    //获取stackMin栈中的栈顶元素，stackMin栈中保存的每一次入栈的最小值
    private int getMin() {
        if (this.stackMin.isEmpty()) {
            throw new RuntimeException("栈中元素为空！");
        }
        // Java利用Stack类的peek()函数获取堆栈中的顶部元素
        return this.stackMin.peek();
    }

}

注意：方法一是更加好的方法