洛谷P1043

[NOIP2003 普及组] 数字游戏

题目描述

丁丁最近沉迷于一个数字游戏之中。这个游戏看似简单，但丁丁在研究了许多天之后却发觉原来在简单的规则下想要赢得这个游戏并不那么容易。游戏是这样的，在你面前有一圈整数（一共 \(n\) 个），你要按顺序将其分为 \(m\) 个部分，各部分内的数字相加，相加所得的 \(m\) 个结果对 \(10\) 取模后再相乘，最终得到一个数 \(k\)。游戏的要求是使你所得的 \(k\) 最大或者最小。

例如，对于下面这圈数字（\(n=4\)，\(m=2\)）：

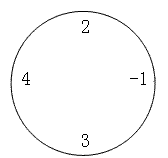
要求最小值时，\(((2-1)\bmod10)\times ((4+3)\bmod10)=1\times 7=7\)，要求最大值时，为 \(((2+4+3)\bmod10)\times (-1\bmod10)=9\times 9=81\)。特别值得注意的是，无论是负数还是正数，对 \(10\) 取模的结果均为非负值。

丁丁请你编写程序帮他赢得这个游戏。

输入格式

输入文件第一行有两个整数，\(n\) （\(1\le n\le 50\)） 和 \(m\) （\(1\le m\le 9\)）。以下 \(n\) 行每行有个整数，其绝对值 \(\le10^4\)，按顺序给出圈中的数字，首尾相接。

输出格式

输出文件有 \(2\) 行，各包含 \(1\) 个非负整数。第 \(1\) 行是你程序得到的最小值，第 \(2\) 行是最大值。

样例 #1

样例输入 #1

4 2
4
3
-1
2

样例输出 #1

7
81

提示

【题目来源】

NOIP 2003 普及组第二题

事实证明，当你想不出状态方程时，记忆化搜索是一个不错的思路

//                  （ᗜ ‸ ᗜ）
//           去吧，鸭鸭，把希儿和AC都带回来！
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
const int INF = 0x3f3f3f3f3f3f3f3f;
int n, m;
int s[105];
int pre[105];
int dp[10][105][105][2];
int minn = INF;
int maxx = -INF;
void dfs(int id, int ls, int rs, int res, int fr)
{

    int sum = pre[rs] - pre[ls - 1];
    sum = (sum%10+10)%10;
    res = res * sum;
    int i = rs + 1;
    if (id == m)
    {
        maxx = max(res, maxx), minn = min(res, minn);
        return;
    }
    int flag1 = 0,flag2 = 0;

    if (dp[id][fr][rs][0] <= res)
        {
            flag1 = 1;
        }
    else
        dp[id][fr][rs][0] = res;
    if (dp[id][fr][rs][1] >= res){
        flag2 = 1;
    }
    else
        dp[id][fr][rs][1] = res;
    if(flag1 && flag2) return;
    if (id == m - 1)
    {
        dfs(id + 1, i, fr + n - 1, res, fr);
        return;
    }
    for (int j = i; n + fr - j >= m - id; j++){
        dfs(id + 1, i, j, res, fr);
    }
}
inline int read()
{
    int x = 0, f = 1;
    char ch = getchar();
    while (ch < '0' || ch > '9')
    {
        if (ch == '-')
            f = -1;
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9')
    {
        x = x * 10 + ch - '0';
        ch = getchar();
    }
    return x * f;
}
inline void print(int x)
{
    if (x < 0)
    {
        putchar('-');
        x = -x;
    }
    if (x > 9)
        print(x / 10);
    putchar(x % 10 + '0');
}
signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cin >> n >> m;
    for(int i = 1; i <= m; i++){
        for(int j = 1; j <= 2 * n; j++){
            for(int k = 1; k <= 2 * n; k++){
                dp[i][j][k][0] = INF;
                dp[i][j][k][1] = -INF;
            }
        }
    }
    for (int i = 1; i <= n; i++)
        cin >> s[i], s[i + n] = s[i];
    for (int i = 1; i <= 2 * n; i++)
        pre[i] = pre[i - 1] + s[i];
    if (m == 1)
    {
        dfs(1, 1, n, 1, 1);
    }
    else{
    for (int i = 1; i <= n; i++)
        for (int j = i; n + i - j >= m; j++)
            dfs(1, i, j, 1, i);
    }
    cout << minn << endl;
    cout << maxx << endl;
    return 0;
}