【LeetCode回溯算法#11】解数独，这次是真的用回溯法处理二维数组

解数独

力扣题目链接(opens new window)

编写一个程序，通过填充空格来解决数独问题。

一个数独的解法需遵循如下规则： 数字 1-9 在每一行只能出现一次。 数字 1-9 在每一列只能出现一次。 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。 空白格用 '.' 表示。

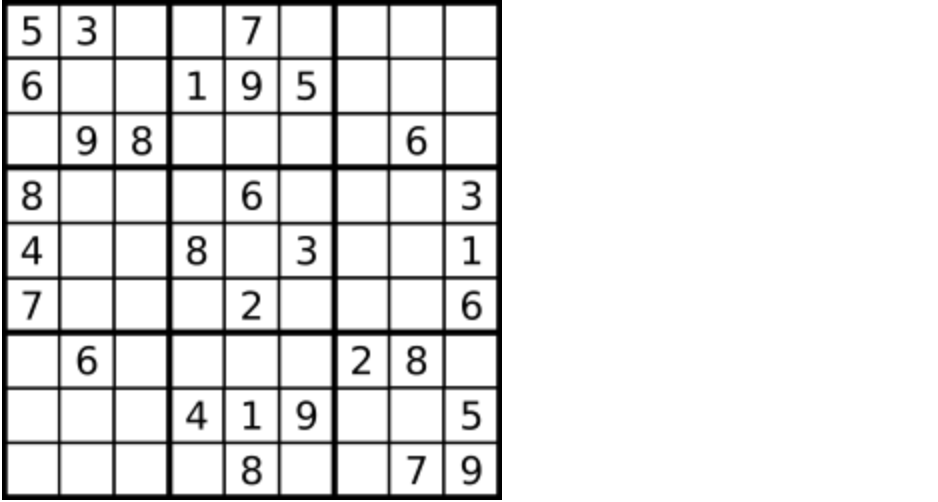
示例 1：

输入：board = [
["5","3",".",".","7",".",".",".","."],
["6",".",".","1","9","5",".",".","."],
[".","9","8",".",".",".",".","6","."],
["8",".",".",".","6",".",".",".","3"],
["4",".",".","8",".","3",".",".","1"],
["7",".",".",".","2",".",".",".","6"],
[".","6",".",".",".",".","2","8","."],
[".",".",".","4","1","9",".",".","5"],
[".",".",".",".","8",".",".","7","9"]]

输出：[["5","3","4","6","7","8","9","1","2"],
["6","7","2","1","9","5","3","4","8"],
["1","9","8","3","4","2","5","6","7"],
["8","5","9","7","6","1","4","2","3"],
["4","2","6","8","5","3","7","9","1"],
["7","1","3","9","2","4","8","5","6"],
["9","6","1","5","3","7","2","8","4"],
["2","8","7","4","1","9","6","3","5"],
["3","4","5","2","8","6","1","7","9"]]

解释：输入的数独如上图所示，唯一有效的解决方案如下所示：

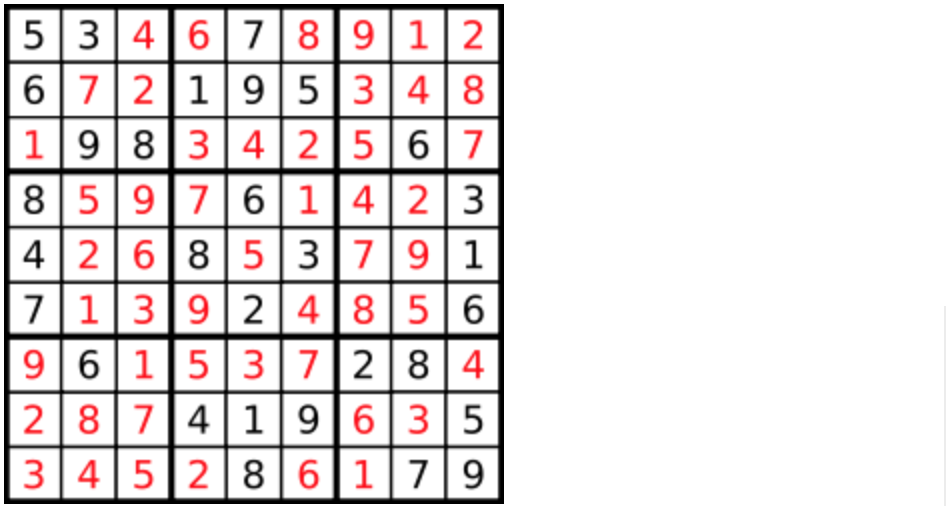
提示：

• 给定的数独序列只包含数字 1-9 和字符 '.' 。
• 你可以假设给定的数独只有唯一解。
• 给定数独永远是 9x9 形式的。

思路

看似跟N皇后差不多，好像也可以通过一层一层的递归进行遍历，然后填满所有空格

但是区别还是挺大的（反正用同样的思路是做不出来这题的）

从数独规则的角度来捋一捋解题思路

我们需要做的是去遍历"数独棋盘"，该棋盘由9个3X3的小九宫格组成

往"数独棋盘"的每个空里面填数字，要求是同行列中不能出现与之相同的数

注意，我们每次填数字的对象都是"数独棋盘"，也就是说，我们在一个递归层中需要处理的是一个二维数组，这就是本题与N皇后的区别

因此，在单层递归中需要引入两个for循环，一个负责遍历行，一个负责遍历列，这样才能定位"数独棋盘"中一个待填的格子，进而判断其中有没有数、需不需要填数、填的数合不合法

代码分析

基于上述分析，还是先来三部曲

三部曲

1、确定回溯函数的参数和返回值

题目的提示说了可以假定只有一个解，意思就是说我们不需要获取数独的所有可能解

那么，碰到（或者说填完）一个符合条件的解之后我们就应该立刻返回

是不是有点熟悉，没错，这种情况时，递归函数的返回值应该设置为布尔值，并且需要接受返回结果（详见路径总和）

而回溯函数的输入参数是"数独棋盘"，不需要别的参数，因为本质上是去做一系列修改board的操作

class Solution {
private:
    //确定回溯函数的参数和返回值
    bool backtracking(vector<vector<char>>& board){
    }
public:
    void solveSudoku(vector<vector<char>>& board) {
    }
};

2、确定终止条件

因为我们是要填满"数独棋盘"的每个格子，所以其实不需要终止，只要for循环结束就会自动终止，此时如果填完了就是找到一个结果，没填完就是当前数独无解

class Solution {
private:
    //确定回溯函数的参数和返回值
    bool backtracking(vector<vector<char>>& board){
        //(确定终止条件，其实这里是不需要的)
    }
public:
    void solveSudoku(vector<vector<char>>& board) {
    }
};

3、确定单层处理逻辑

这里就是本题的核心了，我们需要在这里遍历整个"数独棋盘"，即遍历它的行和列

自然的，这需要使用两个for来完成

在for循环的最里层，先判断当前拿到的格子是不是空的，不是就跳过不用填，是就继续之后的逻辑

我们需要进行填数的逻辑，此时需要遍历数字1~9，判断当前通过两层for拿到的空格子应该填入哪个数字

这里是不是又很熟悉，没错，又的需要一个判断函数isVaild来对填入的数进行规则判断（详见n皇后，不过这里两者没有联系）

这部分的总体步骤如下：

​ 1、遍历行，即board里的元素

​ 2、遍历列，即board里元素的元素（二维数组里的数组元素里的数值元素）

​ 3、判断当前格子是否为空（空跳过，不空继续）

​ 4、遍历1~9看哪个数合适填入

​ ·每次遍历均使用规则判断函数进行判定

​ ·返回true就填入当前数

​ 5、触发递归，并接受递归函数的返回值，为true那本层也返回true

​ 6、回溯，结束

class Solution {
private:
    //确定回溯函数的参数和返回值
    bool backtracking(vector<vector<char>>& board){
        //(确定终止条件，其实这里是不需要的)

        //确定单层处理逻辑
        //两层for分别遍历行和列
        for(int i = 0 ; i < board.size(); ++i){//遍历行，即board里的元素
            for(int j = 0; j < board[0].size(); ++j){//遍历列，即board里元素的元素
                if(board[i][j] != '.') continue;//当前格有值就跳过
                //判断当前位置放1~9哪个数合适
                for(char k = '1'; k <= '9'; ++k){
                    //判断当前格放k是否合适
                    if(isVaild(i, j, k, board)){//合适就放
                        board[i][j] = k;
                        if(backtracking(board)) return true;//注意了，这里是需要处理返回值的
                        board[i][j] = '.';
                    }
                }
                return false;//在当前空中判断1~9都不适合填入，那就是无解，直接返回false
            }
        }
        return true;//遍历完所有格子没返回false，就说明填完了
    }
public:
    void solveSudoku(vector<vector<char>>& board) {
    }
};

在写这部分代码时有以下注意事项：

​ 1、要是捣不清现在是行还是列，就去题目给的实例看一下（注释里也有写）

​ 2、递归时需要处理返回值

规则判断函数isVaild

判断棋盘是否合法有如下三个维度：

• 同行是否重复
• 同列是否重复
• 9宫格里是否重复

这里很容易把第三种情况漏掉，请特别注意一下

	//规则判断函数，实现数独规则判定
    bool isVaild(int row, int col, int curValue, vector<vector<char>>& board){
        //在整个数独棋盘范围上
        //判断行里是否有与curValue重复的值
        for(int i = 0; i < 9; ++i){
            if(board[row][i] == curValue) return false;
        }

        //判断列里是否有与curValue重复的值
        for(int j = 0; j < 9; ++j){
            if(board[j][col] == curValue) return false;
        }

        //在数独棋盘中的3X3的九宫格上
        //设置每个小九宫格开始遍历的位置（每三个空格为一个小九宫格）
        int miniblockRow = (row / 3) * 3;
        int miniblockCol = (col / 3) * 3;

        //判断小九宫格里有无重复值
        for(int i = miniblockRow; i < miniblockRow + 3; ++i){//注意遍历条件，一次跳3格
            for(int j = miniblockCol; j < miniblockCol + 3; ++j){
                if(board[i][j] == curValue) return false;
            }
        }
        return true;
    }

再刷如果有问题再补充，TBD（23:00了我顶不住了）

完整代码

class Solution {
private:
    //确定回溯函数的参数和返回值
    bool backtracking(vector<vector<char>>& board){
        //(确定终止条件，其实这里是不需要的)

        //确定单层处理逻辑
        //两层for分别遍历行和列
        for(int i = 0 ; i < board.size(); ++i){//遍历行，即board里的元素
            for(int j = 0; j < board[0].size(); ++j){//遍历列，即board里元素的元素
                if(board[i][j] != '.') continue;//当前格有值就跳过
                //判断当前位置放1~9哪个数合适
                for(char k = '1'; k <= '9'; ++k){
                    //判断当前格放k是否合适
                    if(isVaild(i, j, k, board)){//合适就放
                        board[i][j] = k;
                        if(backtracking(board)) return true;
                        board[i][j] = '.';
                    }
                }
                return false;//在当前空中判断1~9都不适合填入，那就是无解，直接返回false
            }
        }
        return true;//遍历完所有格子没返回false，就说明填完了
    }
    //规则判断函数，实现数独规则判定
    bool isVaild(int row, int col, int curValue, vector<vector<char>>& board){
        //在整个数独棋盘范围上
        //判断行里是否有与curValue重复的值
        for(int i = 0; i < 9; ++i){
            if(board[row][i] == curValue) return false;
        }

        //判断列里是否有与curValue重复的值
        for(int j = 0; j < 9; ++j){
            if(board[j][col] == curValue) return false;
        }

        //在数独棋盘中的3X3的九宫格上
        //设置每个小九宫格开始遍历的位置（每三个空格为一个小九宫格）
        int miniblockRow = (row / 3) * 3;
        int miniblockCol = (col / 3) * 3;

        //判断小九宫格里有无重复值
        for(int i = miniblockRow; i < miniblockRow + 3; ++i){
            for(int j = miniblockCol; j < miniblockCol + 3; ++j){
                if(board[i][j] == curValue) return false;
            }
        }
        return true;
    }
public:
    void solveSudoku(vector<vector<char>>& board) {
        backtracking(board);
    }
};