P9073 [WC/CTS2023] 楼梯 题解

题目链接

简要题意

有一块楼梯，这里指的楼梯是倒着的，正过来看上一层宽度一定小于等于这一层宽度，并且由格子组成，你需要对其进行增删和恢复某一历史版本的操作，并回答这块楼梯是否有固定格数的子楼梯。

题目分析

看到题目，平面，带修改查询，范围 \(10^9\)，真是 buff 叠满了，似乎非常难以入手。

从特殊性质条件入手呢？此题给了很多特殊的性质，但是从它们相关的适用范围入手似乎都不是很好考虑，我们只好退而求其次，想想我们有什么能用的思考方式。

首先考虑归约问题，把题目中一些难以入手的问题转化为已知问题，本题中最大的难点就在于修改是对于整个平面的，况且范围过大，无法使用数据结构进行维护。

我们从较为简单的修改开始考虑，构造几个楼梯试着改一改，可以发现在这种更改信息下，貌似只是对于某个行区间的列数进行了区间增加，从这点出发，就可以把删的操作分解，看做区间推平和区间减法，即可把修改变为对于一个线段树的维护。

那最重要的询问呢，发现无处入手，我们换种思考方式，想想怎么简化问题，因为有了因数这一重要的约束条件，我们从小范围入手，看看能不能从一些特殊规律方面进行简化。先看当 \(p=q/2\) 时会发生什么，看题目所给的图，发现可行解的边界左端点构成了一个区间，这是不是我们想要的性质呢？

继续构造数据，发现虽然上述性质被否定了，但是可以发现另外一个性质，好像一个楼梯中总有一个以最右上方或左下方格子为边界的解，不要慌，想想我们能不能证明它。

边界边界，有什么性质吗，通过刚才的一通操作，再结合初看题目时的生成格，想必大家也能发现一个明显的条件，把生成格看做一个激光发射器，它垂直或平行射出的射线一定是穿透的，且它的楼梯所有的格子都在这里面，也就是说，一个子楼梯把左边界和上边界排除，一定是右边界开下边界结束（可能有点抽象，可以看图理解一下），而刚才说到的那两个格子贡献的也刚好是这两个边界！

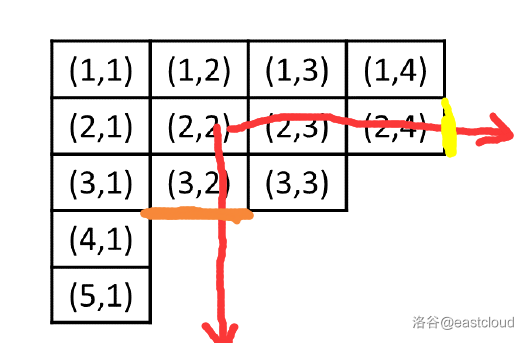
再反过来看，两个这样的边界甚至可以确定一个唯一的子楼梯！而边界的集合也可以排出一个序列，也可以我们像刚才那样维护修改，转化成边界后，看似无用的因数一条件也可以派上用场了。

继续证明上述结论，可以发现在 \(p=q/2\) 时，子楼梯另外一个边界序号都相同，要是不是上边界就配合下面的，否则可以跟上面的配对，能继续推广吗，发现这个操作本质上是一种范围的缩小，当 \(qk=p\) 时，每次通过取中点可以排除一半的区间，进而找到答案。

上述操作也能在维护边界的线段树上二分实现，于是，我们通过常用的思维模式，解决了这道看似复杂的思维问题，希望读者在做题时，也可以多尝试用归约，分解，简化等方式进行思考（这实际上摘自《线性代数入门》中的绪论部分，感觉蛮有效的就搬过来了）。

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define maxn 1000000000
#define ll long long
#define N 300005
using namespace std;
ll tot,rt[N];
struct Node{
	ll ls,rs,sum;
	#define ls(x) tr[x].ls
	#define rs(x) tr[x].rs
	#define s(x) tr[x].sum
}tr[N<<5];
ll read(){
	ll x=0,f=1;
	char ch=getchar();
	while(ch<'0' || ch>'9'){
		if(ch=='-') f=-1;
		ch=getchar();
	}
	while(ch>='0' && ch<='9'){
		x=(x<<1)+(x<<3)+(ch^48);
		ch=getchar();
	}
	return x*f;
}
void change(ll &x,ll l,ll r,ll p,ll val){
	ll np=x;x=++tot;tr[x]=tr[np];s(x)+=val;
	if(l==r) return;
	ll mid=(l+r)>>1;
	if(p<=mid) change(ls(x),l,mid,p,val);
	else change(rs(x),mid+1,r,p,val);
	s(x)=s(ls(x))+s(rs(x));
}
ll query(ll x,ll l,ll r,ll L,ll R){
	if(!x || (L>=l && R<=r)) return s(x);
	ll mid=(L+R)>>1;ll ans=0;
	if(l<=mid) ans+=query(ls(x),l,r,L,mid);
	if(r>mid) ans+=query(rs(x),l,r,mid+1,R);
	return ans;
}
void clear(ll &x,ll l,ll r,ll L,ll R){
	if(!x) return;if(L>=l && R<=r){x=0;return;}
	ll np=x;x=++tot;tr[x]=tr[np];
	ll mid=(L+R)>>1;
	if(l<=mid) clear(ls(x),l,r,L,mid);
	if(r>mid) clear(rs(x),l,r,mid+1,R);
	s(x)=s(ls(x))+s(rs(x));
}
ll find_pos(ll x,ll l,ll r,ll val){
	if(l==r) return l;
	ll mid=(l+r)>>1;
	if(s(rs(x))>=val) return find_pos(rs(x),mid+1,r,val);
	else return find_pos(ls(x),l,mid,val-s(rs(x)));
}
ll find_x(ll x,ll val,ll l,ll r){
	if(l==r) return val==1?l:-l;
	ll mid=(l+r)>>1;
	if(mid-l+1+s(ls(x))>=val) return find_x(ls(x),val,l,mid);
	else return find_x(rs(x),val-(mid-l+1)-s(ls(x)),mid+1,r);
}
void solve(ll val,ll l,ll r,ll rt){
	if(l==r-1){
		ll p=find_x(rt,l*val+1,1,maxn),q=-find_x(rt,r*val+1,1,maxn);
		cout<<p<<' '<<query(rt,p,maxn,1,maxn)-(val+p-q)+1<<endl;
		return;
	}
	ll mid=(l+r)>>1;
	if(find_x(rt,mid*val+1,1,maxn)>0) solve(val,mid,r,rt);
	else solve(val,l,mid,rt);
}
int main(){
	ll m,a,b;char opt;
	m=read();
	for(ll i=1;i<=m;i++){
		rt[i]=rt[i-1];
		cin>>opt;a=read();
		if(opt=='+'){b=read();change(rt[i],1,maxn,a,b);}
		else if(opt=='R') rt[i]=rt[i-a-1];
		else if(opt=='-'){
			b=read();
			ll sum=query(rt[i],a,maxn,1,maxn);
			if(sum<b){
				clear(rt[i],a,maxn,1,maxn);
				if(a!=1) change(rt[i],1,maxn,a-1,sum);
			}
			else{
				ll p=find_pos(rt[i],1,maxn,b);
				ll tmp=query(rt[i],p+1,maxn,1,maxn);
				clear(rt[i],p+1,maxn,1,maxn);
				change(rt[i],1,maxn,p,tmp-b);
				if(a!=1) change(rt[i],1,maxn,a-1,b);
			}
		}
		else if(opt=='?'){
			if(s(rt[i])==0){cout<<-1<<' '<<-1<<endl;continue;}
			ll k=find_pos(rt[i],1,maxn,1);
			ll sum=k-1+s(rt[i]);
			solve(a,0,sum/a,rt[i]);
		}
	}
}