UVA 11731 Ex-circles （外切圆）

题意：给你三角形的三条边，求图中DEF的面积和阴影部分的面积。

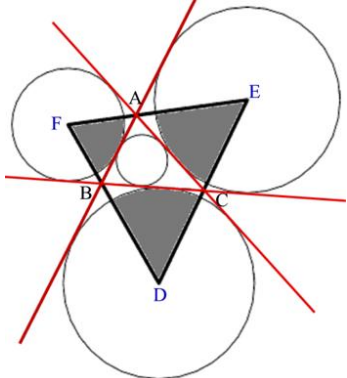
题解：一些模板，三角形的旁切圆半径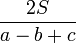：、与

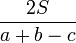
三旁心为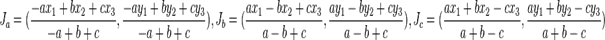

#include<set>
#include<map>
#include<queue>
#include<stack>
#include<cmath>
#include<vector>
#include<string>
#include<cstdio>
#include<cstring>
#include<iomanip>
#include<stdlib.h>
#include<iostream>
#include<algorithm>
using namespace std;
#define eps 1E-8
/*注意可能会有输出-0.000*/
#define Sgn(x) (x<-eps? -1 :x<eps? 0:1)//x为两个浮点数差的比较,注意返回整型
#define Cvs(x) (x > 0.0 ? x+eps : x-eps)//浮点数转化
#define zero(x) (((x)>0?(x):-(x))<eps)//判断是否等于0
#define mul(a,b) (a<<b)
#define dir(a,b) (a>>b)
typedef long long ll;
typedef unsigned long long ull;
const int Inf=<<;
const ll INF=1ll<<;
const double Pi=acos(-1.0);
const int Mod=1e9+;
const int Max=;
struct point
{
    double x,y;
}poi[Max];
double ans1,ans2;
double Jud(double a,double b,double c)
{
    //cout << a*a+b*b-c*c <<  " " << 2*a*b << endl;
    return acos((a*a+b*b-c*c)/(*a*b));
}
double Dis(point p1,point p2)
{
    return sqrt((p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y));
}
void Solve(double a,double b,double c)
{
    double x1,y1,x2,y2,x3,y3,href;
    href=(a+b+c)/;
    double S=sqrt(href*(href-a)*(href-b)*(href-c));
    x3=y3=x2=;
    y2=a;
    y1=(a*a+b*b-c*c)/(*a);
    x1=sqrt(b*b-y1*y1);
    poi[].x=(-a*x1+b*x2+c*x3)/(-a+b+c);
    poi[].y=(-a*y1+b*y2+c*y3)/(-a+b+c);
    poi[].x=(a*x1-b*x2+c*x3)/(a-b+c);
    poi[].y=(a*y1-b*y2+c*y3)/(a-b+c);
    poi[].x=(a*x1+b*x2-c*x3)/(a+b-c);
    poi[].y=(a*y1+b*y2-c*y3)/(a+b-c);
    double aa=Dis(poi[],poi[]);
    double bb=Dis(poi[],poi[]);
    double cc=Dis(poi[],poi[]);
    href=(aa+bb+cc)/;
    ans1=sqrt(href*(href-aa)*(href-bb)*(href-cc));
    double r1=(*S)/(-a+b+c);
    double r2=(*S)/(a-b+c);
    double r3=(*S)/(a+b-c);
    //cout << aa << " " << bb << " " << cc <<endl;
    ans2=(Jud(bb,cc,aa)/)*r1*r1;
    ans2+=(Jud(aa,bb,cc)/)*r2*r2;
    ans2+=(Jud(cc,aa,bb)/)*r3*r3;
    return;
}
int main()
{
    int a,b,c;
    int coun=;
    while(~scanf("%d %d %d",&a,&b,&c))
    {
        if(!a&&!b&&!c)
            break;
        Solve((double)a,(double)b,(double)c);
     printf("Case %d: %.2f %.2f\n",++coun,ans1,ans2);
    }
    return ;
}