LeetCode：下一个排列【31】

LeetCode：下一个排列【31】

题目描述

实现获取下一个排列的函数，算法需要将给定数字序列重新排列成字典序中下一个更大的排列。

如果不存在下一个更大的排列，则将数字重新排列成最小的排列（即升序排列）。

必须原地修改，只允许使用额外常数空间。

以下是一些例子，输入位于左侧列，其相应输出位于右侧列。
1,2,3 → 1,3,2
3,2,1 → 1,2,3
1,1,5 → 1,5,1

题目分析

什么样的排列将产生下一个更大的数字呢？

　　

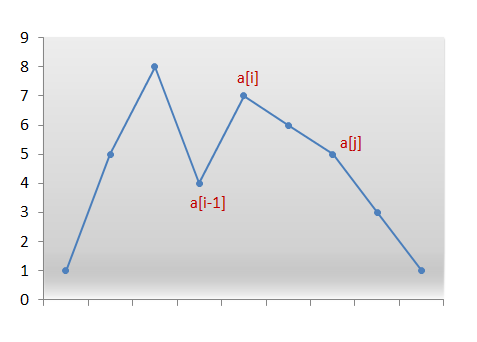
　　观察上面这个图，我们需要将数字 a[i-1]替换为位于其右侧区域的数字中比它更大的数字，例如 a[j]。我们交换数字 a[i-1]和 a[j]。我们现在在索引 i-1处有正确的数字。

　　但目前的排列仍然不是我们正在寻找的排列。我们需要通过仅使用 a[i-1]右边的数字来形成最小的排列。因此，我们需要放置那些按升序排列的数字，以获得最小的排列。

具体的操作如下：

　　

Java题解

class Solution {
    public void nextPermutation(int[] nums) {
        int i = nums.length-2;
        while(i>=0&&nums[i+1]<=nums[i])
            i--;
        if(i>=0)
        {
            int j = nums.length-1;
            while(j>=0&&nums[j]<=nums[i])
                j--;
            swap(nums,i,j);
        }
        reverse(nums,i+1);

    }

    private void reverse(int[] nums, int start) {
        int i = start, j = nums.length - 1;
        while (i < j) {
            swap(nums, i, j);
            i++;
            j--;
        }
    }

    private void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
}