HGOI20180814 （NOIP 模拟Day1）

100pts=40+60+0

rank 56

若串联那么显然是这样：

若并联那么显然是这样：

串联时C＜1，并联时C>1，贪心策略＜1时尽可能串联，>1时尽可能并联

考虑这样一个数学问题

令0<a<b，那么 a/b<1 ,设前面串联的电容为X，那么就有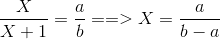  

迭代的话就是用b-a代替b，ans++,这里做一个优化，就是当a小b大的时候无法快速让a>b这里用取膜，

举个例子 2/11--2/9--2/7--2/5--2/3--2/1要经过5次才到a>b那我这五次可以压缩成1次计算 注意到 11/2就是5次 11%2=1余数

那么迭代的话就是ans+=b/a;a'=a;b'=a%b;

令0<b<a，那么a/b>1，尽可能用并联累加这样最多累加次数是a/b，余数是(a%b)/b

累加的话ans+=a/b迭代的话就是a'=a%b;b'=b;

注意一个问题a==0或者b==0的情况需要及时return否则会RE！！！

# include <bits/stdc++.h>
using namespace std;
long long ans;
void fun(long long a,long long b)
{
    if (a==||b==) return;
    if (a%b==) {ans+=a/b; return;}
    if (a==) { ans+=b; return;}
    if (b==) { ans+=a; return;}
    if (a<b)  { ans+=b/a; fun(a,b%a);}
     //if (a<b) {ans++; fun(a,b-a); }
    if (a>b)  { ans+=a/b; fun(a%b,b);}
}
int main()
{
    freopen("capacitor.in","r",stdin);
    freopen("capacitor.out","w",stdout);
    int T; scanf("%d",&T);
    long long a,b;
    while (T--) {
        scanf("%lld%lld",&a,&b);
        ans=0ll;
        fun(a,b);
        printf("%lld\n",ans);
    }
    return ;
}

考虑部分分对于50pts 复杂度 2^T就能过，对于10ptsT是奇数那么就是不能回到地面结果就是0，

那么现在早10min内就有60pts

贴下代码：

# include <bits/stdc++.h>
using namespace std;
const int MAXN=,mo=;
int a[MAXN],t[MAXN],ans,T,len;
char s[MAXN];
bool check()
{
    for (int i=;i<=T-len+;i++) {
        bool flag=true;
        int p=;
        for (int j=i;j<=i+len-;j++,p++)
         if (t[p]!=a[j]) { flag=false;  break;}
        if (flag) return true;
    }
    return false;
}
void dfs(int dep,int k)
{
    if (dep<) return;
    if (dep>T-k+) return;
    if (k>T) {
      if (dep!=) return;
      if (check())ans=(ans+)%mo;
      return;
     }
    a[k]=; dfs(dep-,k+);
    a[k]=; dfs(dep+,k+);
}
int main()
{
    freopen("track.in","r",stdin);
    freopen("track.out","w",stdout);
    scanf("%d",&T);
    if (T%==) { printf("0\n");return ; }
     scanf("%s",s);
    len=strlen(s);
    for (int i=;i<len;i++)
        if (s[i]=='U') t[i+]=;
        else t[i+]=;
    ans=;
    dfs(,);
    printf("%d\n",ans%mo);
    return ;
}

考虑100pts，这道题目显然是dp题，

考虑状态：

dp[i][j]表示前i个岔路，高度为j的合法情况数（就是不到地面以下的情况总数）

f[i][j]表示前i个岔路，高度为j的让猫摔倒（1次或多次）的情况总数

g[i][j]表示前i个岔路，高度为j让猫摔且仅摔一次的情况总数

我们设猫摔倒的情况UD串长度为l，最低处的绝对值（就是从后面走到摔倒序列中最高处）为nn

考虑这样一个事情，假设在第i个岔路高度为j此时猫摔倒了，那么开始摔倒的位置必须是 i-l ,

现在的高度h加上最大的nn必须要大于开始时的高度need+1否则就从地底下上来了（这里设地面高度为1）

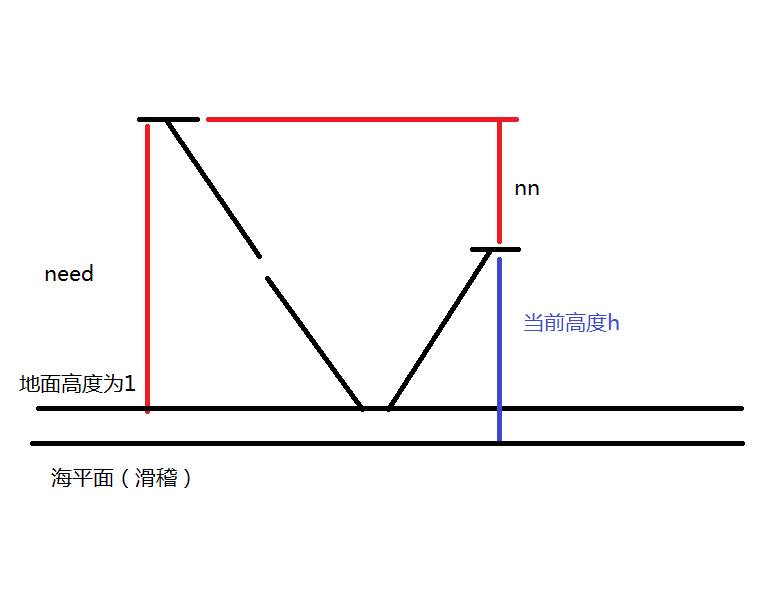
转移：首先最简单的转移：

dp[i][h]=dp[i-1][h-1]+dp[i-1][h+1];
f[i][h]=f[i-1][h-1]+f[i-1][h+1];

后面考虑这样一个问题假设UDUD是猫的摔倒序列，

如果这样一般转移是在前面UDUD UD时+1，UDUD UD时又+1，导致输出比std大

所以运用容斥原理，我们要把多的一部分减掉

首先找出所有的前缀和后缀相同的情况

这里的前缀和后缀举个例子来说是这样的

UDUDDUDU

所有的前缀后缀的对为(U,U)(UDU,UDU)

然后用上我们的g数组在这个区间里面所有前缀只摔一次的可能全部减掉那么就是这个g[i][h]的值

这里的lt表示每一个缀的长度，nt表示每一个缀的最低点（后面推前面的最大值）

            if(i>=l&&h+nn>=need+){
                g[i][h]=dp[i-l][h+nn]-f[i-l][h+nn];
                for(int j=;j<lt.size();j++) g[i][h]-=g[i-(l-lt[j])][h+nt[j]];
            }

然后用g数组更新f数组 f[i][h]+=g[i][h];

程序在这里qwq

#include<bits/stdc++.h>
#define ll long long
#define mod 1000000007
using namespace std;
int n,need,l,nn,cnt;
ll dp[][],f[][],g[][];
char c[];
vector<int> lt,nt;
int main(){
    freopen("track.in","r",stdin);
    freopen("track.out","w",stdout);
    scanf("%d",&n);
    if(n%==){
        printf("");
        return ;
    }
    scanf("%s",c);
    l=strlen(c);
    for(int i=;i<l;i++){
        if(c[i]=='U') nn--;
        else nn++;
        need=max(need,nn); //求出最大的nn，这里的nn为了计算方便是后面到前面相当于前面到后面最小值
    }
    int kk=;
    for(int i=;i<l;i++){
        if(c[i]=='U') kk--;
        else kk++; //这里额kk含义和nn含义一样求法一样
        bool flag=true; //判断此前缀是否和某一后缀匹配
        for(int j=;j<=i;j++){ //枚举前后缀长度
            if(c[j]!=c[l-i+j-]){
                flag=false;
                break;
            }
        }
        if(flag&&i!=l-){ // 注意后缀长度不能为字符串长度
            lt.push_back(i+); //前后缀的长度lt
            nt.push_back(nn-kk); //前后缀的高度与摔跤序列最大值的差
        }
    }
    dp[][]=1ll; //初始化前0个岔路高度为1可能性为1（设地面高度为1）
    for(int i=;i<=n;i++){
        for(int h=;h<=min(i+,n-i+);h++){ //最终要回到终点，如果后面都D都不能到终点就不考虑
            dp[i][h]=dp[i-][h-]+dp[i-][h+];
            f[i][h]=f[i-][h-]+f[i-][h+]; //一般转移
            if(i>=l&&h+nn>=need+){
                g[i][h]=dp[i-l][h+nn]-f[i-l][h+nn]; //前面的总可能减去多种可能的就是恰好在i-l到i这一段摔得结果但是可能存在摔多跤的情况出现
                for(int j=;j<lt.size();j++) g[i][h]-=g[i-(l-lt[j])][h+nt[j]];
                    //在（i,h）刚好摔跤的真正数目原来有重复的要减去中间前后缀摔跤数，就是没有前后缀摔跤数（于是成功的排除多跤计算多次的干扰）
            }
            f[i][h]+=g[i][h]; //加回f中去
            dp[i][h]=dp[i][h]%mod;
            f[i][h]=f[i][h]%mod;
            g[i][h]=g[i][h]%mod;
        }
    }
    printf("%lld",f[n][]);
}

但是std用了KMP？？？

#include<bits/stdc++.h>
using namespace std;
const int mod = ;
const int MAXN = ;
int n, dp[MAXN][MAXN][MAXN];
char s[MAXN]; int slen;
int fail[MAXN][], nxt[MAXN];
void getFail(){
    int j = ;
    nxt[] = nxt[] = ;
    for(int i = ; i < slen; i++){
        while(j >  && s[i] != s[j]) j = nxt[j];
        if(s[i] == s[j]) j++;
        nxt[i + ] = j;
    }
    //printf("len = %d\n", slen);
    if (s[] == 'U') fail[][] = ;
    if (s[] == 'D') fail[][] = ;
    for(int i = ; i <= slen; i++){
        int pos = i;
        while(pos && s[pos] != 'U') pos = nxt[pos];
        fail[i][] = pos + ;
        if(pos ==  && s[] == 'D') fail[i][] = ;

        pos = i;
        while(pos && s[pos] != 'D') pos = nxt[pos];
        fail[i][] = pos + ;
        if(pos ==  && s[] == 'U') fail[i][] = ;
        //printf("i = %d %d %d\n", i, fail[i][0], fail[i][1]);
    }
}

int main(){
    //freopen("track.in", "r", stdin);
    //freopen("track.out", "w", stdout);
    scanf("%d%s", &n, s);
    if(n & ) return puts(""), ;
    n /= ;
    slen = strlen(s);
    getFail();
    dp[][][] = ;
    for(int i = ; i <  * n; i++){
        for(int j = ; j <= n; j++){
            for(int k = ; k < slen; k++){
                if(s[k] == 'U'){
                    (dp[i + ][j + ][k + ] += dp[i][j][k]) %= mod;
                    if(j) (dp[i + ][j - ][fail[k][]] += dp[i][j][k]) %= mod;
                }
                else
                if(s[k] == 'D'){
                    (dp[i + ][j + ][fail[k][]] += dp[i][j][k]) %= mod;
                    if(j) (dp[i + ][j - ][k + ] += dp[i][j][k]) %= mod;
                }
            }
            (dp[i + ][j + ][slen] += dp[i][j][slen]) %= mod;
            if(j) (dp[i + ][j - ][slen] += dp[i][j][slen]) %= mod;
        }
    }
    int ans = dp[ * n][][slen];
    cout << ans << endl;
    return ;
}

0pts:

# include <bits/stdc++.h>
using namespace std;
struct rec{
    int pre,to;
};
int tot=,H,n,m;
const int MAXN=*;
int head[MAXN],dep[MAXN],g[MAXN][],w[MAXN][],x[MAXN],ans,fa[MAXN];
int root,q;
bool vis[MAXN];
rec a[MAXN];
inline int read(int &u){
    char ch=getchar();int f=;u=;
    while(ch<''||ch>''){if(ch=='-') f=-;else f=;ch=getchar();}
    while(ch>=''&&ch<=''){u*=;u+=ch-'';ch=getchar();}
}
inline void adde(int u,int v)
{
    a[++tot].pre=head[u];
    a[tot].to=v;
    head[u]=tot;
}
inline void dfs(int u,int depth)
{
    vis[u]=true;
    dep[u]=depth;
    for (register int i=head[u];i!=;i=a[i].pre) {
        int v=a[i].to; if (vis[v]) continue;
        g[v][]=u; w[v][]=x[v];
        dfs(v,depth+);
    }
}
inline void dfsfather(int u)
{
    vis[u]=true;
    for (int i=head[u];i!=;i=a[i].pre)
    {
        int v=a[i].to;
        if (vis[v]) continue;
        fa[v]=u;
        dfsfather(v);
    }
}
inline void init()
{
    memset(g,,sizeof(g));
    memset(w,,sizeof(w));
    memset(vis,false,sizeof(vis));
    dfs(,);
    g[][]=;
    memset(vis,false,sizeof(vis));
    dfsfather(root);
    memset(vis,false,sizeof(vis));
    for (register int j=;j<=;j++)
    for (register int i=;i<=n;i++)
    {
       g[i][j]=g[g[i][j-]][j-];
       w[i][j]=w[w[i][j-]][j-];
    }
}
int LCA(int u,int v)
{
    int sum=;
    if (dep[u]>dep[v]) swap(u,v);
    for (int i=;i>=;i--)
     if (dep[g[v][i]]>=dep[u]) sum=sum+w[v][i],v=g[v][i];
    if (u==v) return sum+x[u];
    for (int i=;i>=;i--)
     if (g[u][i]!=g[v][i])
      sum=sum+w[u][i]+w[v][i],u=g[u][i],v=g[v][i];
    sum=sum+w[u][]+w[v][];
    return sum+x[g[u][]];
}

void dfssum(int u){
    ans+=x[u];
    vis[u]=true;
    for (int i=head[u];i!=;i=a[i].pre)
    {
        int v=a[i].to;
        if (v==fa[u]) continue;
        if (vis[v]) continue;
        dfssum(v);
    }
}
void work()
{
    root=;init();
    int ch,u,t,v;
    while (q--) {
        read(ch);
        if (ch==) {
            read(root);
            memset(vis,false,sizeof(vis));
            memset(fa,,sizeof(fa));
            fa[root]=root;
            dfsfather(root);
        }else if (ch==) {
            read(u);read(t);
             x[u]=t; init();
        }else if (ch==){
            ans=;
            read(u);
            memset(vis,false,sizeof(vis));
            dfssum(u);
            printf("%d\n",ans);
        } else if (ch==){
            read(u);read(v);
            printf("%d\n",LCA(u,v));
        }
    }
}
int main()
{
    freopen("test.in","r",stdin);
    freopen("test.out","w",stdout);
    scanf("%d%d",&n,&q);
    int ch,u,v;
    for (int i=;i<=n-;i++) {
        read(u);read(v);
        adde(u,v); adde(v,u);
    }
    memset(x,,sizeof(x));
    for (int i=;i<=n;i++) scanf("%d",&x[i]);
    work();
    return ;
}

20pts:

#include<queue>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int maxn=1e5+;
struct node{
    int v,nxt;
}edge[maxn<<];
int head[maxn],tot=;
int sum[maxn],root=,ans=,n;
template <typename T>void read(T& x){
    x=;T fl=;char tmp=getchar();
    while((tmp<''||tmp>'')&&tmp!='-') tmp=getchar();
    if(tmp=='-') fl=-fl,tmp=getchar();
    while(tmp>=''&&tmp<='') x=(x<<)+(x<<)+tmp-'',tmp=getchar();
    x*=fl;
    return ;
}
inline void add_edge(int x,int y){
    edge[tot].v=y;
    edge[tot].nxt=head[x];
    head[x]=tot++;
    return;
}
int dfs(int u,int fa,int wh){
    int ret=sum[u];
    for(int i=head[u];i!=-;i=edge[i].nxt){
        int v=edge[i].v;
        if(v==fa) continue;
        ret+=dfs(v,u,wh);
    }
    if(wh==u) ans=ret;
    return ret;
}
int dis[maxn];
inline int bfs(int x,int y){
    queue<int>q;
    q.push(x);
    memset(dis,,sizeof(dis));
    dis[x]=sum[x];
    while(!q.empty()){
        int u=q.front();q.pop();
        for(int i=head[u];i!=-;i=edge[i].nxt){
            int v=edge[i].v;
            if(!dis[v]){
                dis[v]=dis[u]+sum[v];
                q.push(v);
            }
        }
    }
    return dis[y];
}
int dist[maxn],d[maxn],p[maxn][],large;
void dfs_lca(int u,int dep){
    d[u]=dep;
    for(int i=head[u];i!=-;i=edge[i].nxt){
        int v=edge[i].v;
        if(!d[v]){
            p[v][]=u;
            dist[v]=dist[u]+sum[v];
            dfs_lca(v,dep+);
        }
    }
    return;
}
inline void init(){
    memset(d,,sizeof(d));
    dist[root]=sum[root];
    dfs_lca(root,);
    p[root][]=root;
    while(<<large<=n) large++;
    large--;
    for(int i=;i<=large;i++)
        for(int j=;j<=n;j++)
            p[j][i]=p[p[j][i-]][i-];
    return;
}
void change(int u,int fa,int delta){
    dist[u]+=delta;
    for(int i=head[u];i!=-;i=edge[i].nxt){
        int v=edge[i].v;
        if(v==fa) continue;
        change(v,u,delta);
    }
}
inline int lca(int x,int y){
    if(d[x]>d[y]) swap(x,y);
    for(int i=large;i>=;i--)
        if(d[y]-d[x]>=<<i) y=p[y][i];
    if(x==y) return x;
    for(int i=large;i>=;i--)
        if(p[x][i]!=p[y][i]){
            x=p[x][i];
            y=p[y][i];
        }
    return p[x][];
}
int main(){
    freopen("test.in","r",stdin);
    freopen("test.out","w",stdout);
    memset(head,-,sizeof(head));
    int q;
    cin>>n>>q;
    for(int i=;i<n;i++){
        int x,y;
        read(x),read(y);
        add_edge(x,y);
        add_edge(y,x);
    }
    for(int i=;i<=n;i++)
        read(sum[i]);
        while(q--){
            static int opt,x,y;
            read(opt);
            if(opt==){
                read(root);
            }
            else if(opt==){
                read(x);read(sum[x]);
            }
            else if(opt==){
                read(x);
                ans=;
                dfs(root,-,x);
                cout<<ans<<endl;
            }
            else if(opt==){
                read(x),read(y);
                cout<<bfs(x,y)<<endl;
            }
        }
    return ;
}

100pts:

#include<bits/stdc++.h>
#define LL long long
#define PB push_back
using namespace std;
template<typename T> inline void gmax(T &a, T b){a = a > b ? a : b;}
template<typename T> inline void gmin(T &a, T b){a = a < b ? a : b;}
const int MAXN = ;
int n, q, rt, sum;
vector<int> G[MAXN];
int a[MAXN];
int head[MAXN], fa[MAXN], pch[MAXN];
int dep[MAXN], in[MAXN], out[MAXN], tim;
int sz[MAXN];
void dfs(int x, int f){
    dep[x] = dep[f] + ;
    fa[x] = f;
    sz[x] = ;
    int mxsz = , mxid = ;
    for(unsigned i = , siz = G[x].size(); i < siz; i++){
        int y = G[x][i];
        if(y == f) continue;
        dfs(y, x);
        if(sz[y] > mxsz) mxsz = sz[y], mxid = i;
    }
    if(mxsz) swap(G[x][mxid], G[x][]), pch[x] = G[x][];
}
void dfs2(int x, int f, int h){
    in[x] = ++tim;
    head[x] = h;
    bool ff = true;
    for(unsigned i = , siz = G[x].size(); i < siz; i++){
        int y = G[x][i];
        if(y == f) continue;
        dfs2(y, x, ff ? h : y);
        ff = false;
    }
    out[x] = tim;
}
int t[MAXN];
void add(int x, int v){for(; x <= n; x += x & -x) t[x] += v;}
int query(int x){int res = ; for(; x; x -= x & -x) res += t[x]; return res;}
int main(){
    freopen("test.in", "r", stdin);
    freopen("test.out", "w", stdout);
    scanf("%d%d", &n, &q);
    for(int i = ; i < n; i++){
        int u, v;
        scanf("%d%d", &u, &v);
        G[u].PB(v); G[v].PB(u);
    }
    dfs(, );
    dfs2(, , );
    for(int i = ; i <= n; i++) scanf("%d", &a[i]), sum += a[i], add(in[i], a[i]);
    rt = ;
    while(q--){
        int opt;
        scanf("%d", &opt);
        if(opt == ){
            scanf("%d", &rt);
        }
        else if(opt == ){
            int x, v;
            scanf("%d%d", &x, &v);
            sum += v - a[x];
            add(in[x], v - a[x]);
            a[x] = v;
        }
        else if(opt == ){
            int x, ans = ;
            scanf("%d", &x);
            if(x == rt){
                ans = sum;
            }
            else if(in[x] < in[rt] && out[rt] <= out[x]){
                int lsth = ;
                int p = rt;
                while(head[p] != head[x]) lsth = head[p], p = fa[lsth];
                if(p == x) p = lsth; else p = pch[x];
                ans = sum - (query(out[p]) - query(in[p] - ));
            }
            else{
                ans = query(out[x]) - query(in[x] - );
            }
            printf("%d\n", ans);
        }
        else{
            int x, y, ans = ;
            scanf("%d%d", &x, &y);
            while(x != y){
                if(head[x] == head[y]){
                    if(dep[x] > dep[y]) swap(x, y);
                    ans += query(in[y]) - query(in[x]), y = x;
                }
                else{
                    if(dep[head[x]] > dep[head[y]]) swap(x, y);
                    ans += query(in[y]) - query(in[head[y]] - ), y = fa[head[y]];
                }
            }
            ans += a[x];
            printf("%d\n", ans);
        }
    }
    return ;
}