Meet in the middle

搜索是\(OI\)中一个十分基础也十分重要的部分，近年来搜索题目越来越少，逐渐淡出人们的视野。但一些对搜索的优化，例如\(A\)*，迭代加深依旧会不时出现。本文讨论另一种搜索——折半搜索\((meet\ in\ the\ middle)\)。

由一道例题引入：CEOI2015 Day2 世界冰球锦标赛

我们可以用以下代码解决\(n\leq 20\)的数据，时间复杂度\(O(2^n)\)

void dfs(int step, int sum)
{
    if (sum>m) return;
    if (step==n+1) {ans++; return;}
    dfs(step+1, sum+a[step]);
    dfs(step+1, sum);
}

\(dfs\)有何弊端？

当搜索层数增加时，时间复杂度增加过快。

可不可以减少搜索层数，甚至降至一半？

当然可以。不然我这篇文章写什么

看网上两张很好的图就一目了然了。

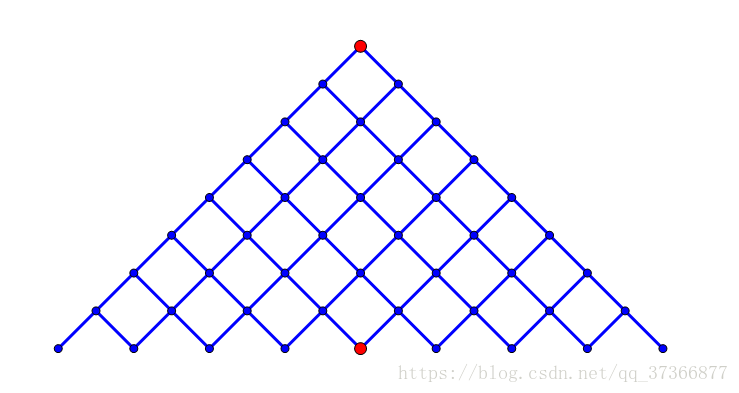
于是我们从\(1\)和\(n\)搜索\(\frac{n}{2}\)的深度，然后得到两个长为\(2^{\frac{n}{2}}\)的序列，对于第一个排序，然后用第二个在第一个中二分查找并统计答案即可。

（此代码不开\(O2\)在洛谷会\(T\)一个点，在\(loj\)跑的飞快，可能是满屏\(vector\)的缘故。）

#pragma GCC optimize (2)
#include<cstdio>
#include<vector>
#include<algorithm>
#define int long long
#define rep(i, a, b) for (register int i=(a); i<=(b); ++i)
#define per(i, a, b) for (register int i=(a); i>=(b); --i)
using namespace std;
const int N=45;
vector<int> a, b;
int c[N], m, ans, n, mid;
inline int read()
{
    int x=0,f=1;char ch=getchar();
    for (;ch<'0'||ch>'9';ch=getchar()) if (ch=='-') f=-1;
    for (;ch>='0'&&ch<='9';ch=getchar()) x=(x<<1)+(x<<3)+ch-'0';
    return x*f;
}
void dfs1(int step, int now)
{
    if (now>m) return;
    if (step>mid) {a.push_back(now); return;}
    dfs1(step+1, now+c[step]);
    dfs1(step+1, now);
}
void dfs2(int step, int now)
{
    if (now>m) return;
    if (step>n) {b.push_back(now); return;}
    dfs2(step+1, now+c[step]);
    dfs2(step+1, now);
}
signed main()
{
    n=read(); m=read(); mid=n+1>>1;
    rep(i, 1, n) c[i]=read();
    dfs1(1, 0); dfs2(mid+1, 0);
    sort(b.begin(), b.end());
    for (int i:a) ans+=upper_bound(b.begin(), b.end(), m-i)-b.begin();
    printf("%lld\n", ans);
    return 0;
}

再来看另一道例题：USACO12OPEN 平衡的奶牛群

可以看看官方题解。

有一种显然的暴力，子集枚举即可， 时间复杂度\(O(3^n)​\)，无法通过。

我们把奶牛分为两组：黑色和白色。若\(S\)可行，那么\(S\)可被分为\(A,B\)，使得\(sum_{A,black}-sum_{B,black}=sum_{B,white}-sum_{A,white}\)。于是我们可以计算黑色牛每一个子集可能的差值，白色同理。然后对于相同的差值进行配对，统计答案即可。

时间复杂度\(O(3^{\frac{n}{2}}\cdot 2^{\frac{n}{2}})\)，即\(O((\sqrt{6})^n)\)，可以通过。

依旧满屏\(vector\)

#include<cstdio>
#include<vector>
#include<algorithm>
#define rep(i, a, b) for (register int i=(a); i<=(b); ++i)
#define per(i, a, b) for (register int i=(a); i>=(b); --i)
using namespace std;
inline int read()
{
    int x=0,f=1;char ch=getchar();
    for (;ch<'0'||ch>'9';ch=getchar()) if (ch=='-') f=-1;
    for (;ch>='0'&&ch<='9';ch=getchar()) x=(x<<1)+(x<<3)+ch-'0';
    return x*f;
}
vector<pair<int, int> > solve(vector<int> S)
{
    vector<pair<int, int> > ans;
    int n=S.size();
    rep(i, 0, (1<<n)-1)
        for (int j=i; ; j=(j-1)&i)
        {
            int sum=0;
            rep(k, 0, n-1)
                if (j&(1<<k)) sum-=S[k];
                    else if (i&(1<<k)) sum+=S[k];
            if (sum>=0) ans.push_back(make_pair(sum, i));
            if (!j) break;
        }
    sort(ans.begin(), ans.end());
    ans.resize(unique(ans.begin(), ans.end())-ans.begin());
    return ans;
}
int main()
{
    int n=read();
    vector<int> P, Q;
    rep(i, 0, n-1)
    {
        int x=read();
        if (i&1) P.push_back(x);
            else Q.push_back(x);
    }
    vector<pair<int, int> > L=solve(P), R=solve(Q);
    int p=0, q=0, l=L.size(), r=R.size();
    vector<bool> vis(1<<n);
    while (p<l && q<r)
    {
        if (L[p].first<R[q].first) p++;
        else if (L[p].first>R[q].first) q++;
        else
        {
            int p2=p, q2=q;
            while (p2<l && L[p2].first==L[p].first) p2++;
            while (q2<r	&& R[q2].first==R[q].first) q2++;
            rep(i, p, p2-1) rep(j, q, q2-1)
                vis[L[i].second|(R[j].second<<P.size())]=true,
            p=p2; q=q2;
        }
    }
    int ans=count(vis.begin()+1, vis.end(), true);
    printf("%d\n", ans);
    return 0;
}

SP4580 ABCDEF

即\(a*b+c=d*(e+f),d\neq 0\)。先枚举前三个，后三个枚举后二分查找即可。

#include<cstdio>
#include<vector>
#include<algorithm>
#define rep(i, a, b) for (register int i=(a); i<=(b); ++i)
#define per(i, a, b) for (register int i=(a); i>=(b); --i)
using namespace std;
vector<int> b, v, w;
int a[105], n; long long ans;
inline int read()
{
    int x=0,f=1;char ch=getchar();
    for (;ch<'0'||ch>'9';ch=getchar()) if (ch=='-') f=-1;
    for (;ch>='0'&&ch<='9';ch=getchar()) x=(x<<1)+(x<<3)+ch-'0';
    return x*f;
}
void prep()
{
	rep(i, 1, n) rep(j, 1, n) rep(k, 1, n)
		b.push_back(a[i]*a[j]+a[k]);
	sort(b.begin(), b.end());
	for (int i=0, j=0; i<b.size(); i=j+1, j++)
	{
		while (j<b.size()-1 && b[j+1]==b[i]) j++;
		v.push_back(b[i]); w.push_back(j-i+1);
	}
}
int check(int x)
{
	int p=lower_bound(v.begin(), v.end(), x)-v.begin();
	if (v[p]==x) return w[p]; else return 0;
}
void calc()
{
	rep(i, 1, n) rep(j, 1, n) rep(k, 1, n)
		if (a[i]) ans+=check((a[j]+a[k])*a[i]);
}
int main()
{
	n=read();
	rep(i, 1, n) a[i]=read();
	prep(); calc();
	printf("%lld\n", ans);
	return 0;
}