[s905l3]性价比神机mgv3000全网首拆，刷armbian实现更多价值！

最近花55淘了一台mgv3000，s905l3，2+16G带蓝牙，真的性价比没得说

S905L3 工艺28nm差于s905l3a 主频1.9Ghz，超频可以达到2Ghz，GPU是Mail450，当服务器跑ha，nas什么都是很不错的。

而且还自带蓝牙，总体性价比比s905l3a系列高多了

按我的方法可以启动，网卡没有问题，但是目前没有显示，没有蓝牙。

等之后我有时间了照着安卓的dtb改一改也许会解决一切，等我的好消息！

不废话了，上教程

0.材料

1. s905l3a的armbian镜像，可以从https://github.com/ophub/amlogic-s9xxx-armbian/releases里下载，或者dl.imzlh.top:7297/镜像/S905/L3A下载。
2. 建议&可选 ttl转usb，例如linux免驱的pl2303
3. S905L3 机器一台
4. 能用的电脑，Linux或者windows都行

1.烧录armbian镜像

下载USBWriter和S905L3A镜像，解压后电脑插好U盘，打开USBWriter写入U盘

2.设置overload和dtb

打开uEnv.txt，将FDT=/dtb/amlogic/meson-g12a-s905l3a-e900v22c.dtb

改为FDT=/dtb/amlogic/meson-gxl-s905l2-x7-5g.dtb

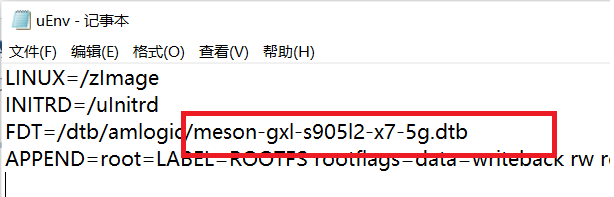
在根目录找到u-boot-p212.bin重命名为u-boot.ext

这下可以正常地启动u盘的armbian了！

3.载入armbian

TTL连接机器或者插好网线，打开ADB或者TELNET登录安卓终端，输入reboot update。

卡住瞬间马上插入u盘，小心提前插入系统文件权限被安卓系统篡改

等待一会去路由器里找到IP地址，名字就是armbian。账号root密码1234

这些图片我是从https://imzlh.top/2022/07/21.php照抄搬来的，反正都一样 搬自己的东西能叫抄吗？

4.安装系统

配置完成后，输入armbian-install no，选0。

除DTB、UBOOT_OVERLOAD选项之外其他的只要回车跳过就行。

知道你们懒癌晚期，直接复制粘贴得了。看，我多贴心

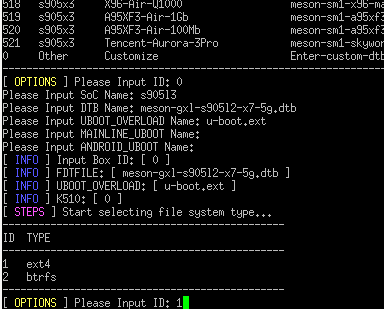
DTB  : meson-gxl-s905l2-x7-5g.dtb
UBOOT: u-boot.ext

接下来，把时间交给reboot。

注意 似乎后期的armbian-install安装成功后会自动更新网卡MAC地址，所以: )之前路由器里找到的IP丢了吧，没用了

5.优化配置

再次ssh登录armbian，我们接下来要改掉s905l3a丑陋的标志和更改更快的源

欢迎页配置：nano /etc/armbian-release

换源 nano /etc/apt/sources.list

我这里提供的是清华源，嫌慢的自行百度吧，我就不一一列举了

Ctrl+\ 输入ports.ubuntu.com 回车 再输入 mirror.tuna.tsinghua.edu.cn/ubuntu-ports，这一步将官方源换成了清华源。

接下来，安装自己喜欢的软件去吧！什么？没有docker？curl -L get.docker.com|sh就行了！

[拆解]全网首拆！MGV3000

MGV3000怎么说呢......还行吧，有串口就是没有SD和USB3...总体来说值得入手

跑码情况：UBOOT太老了，只能挂一个overload勉强U盘启动，不过EMMC就不用挂了。

太长了，点这里下载然后？自己看吧

散热？别提了，配重片（移动官方这么叫的，其实是很大一块散热片）都没有和CPU上的散热片贴合，好大一片空隙。建议爆改一下散热，比如中间垫一块导热硅胶垫什么的