【LeetCode动态规划#10】完全背包问题实战，其三（单词拆分，涉及集合处理字符串）

单词拆分

力扣题目链接(opens new window)

给定一个非空字符串 s 和一个包含非空单词的列表 wordDict，判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词。

说明：

拆分时可以重复使用字典中的单词。

你可以假设字典中没有重复的单词。

示例 1：

输入: s = "leetcode", wordDict = ["leet", "code"]
输出: true
解释: 返回 true 因为 "leetcode" 可以被拆分成 "leet code"。

示例 2：

输入: s = "applepenapple", wordDict = ["apple", "pen"]
输出: true
解释: 返回 true 因为 "applepenapple" 可以被拆分成 "apple pen apple"。
注意你可以重复使用字典中的单词。

示例 3：

输入: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"]
输出: false

思路

如果要往背包问题上靠的话，可以把wordDict中的单词视为"物品"，把字符串s的长度视为背包容量（注意，这里说的是长度，即s.size）

思路听上去很常规,但是具体到实现方式上就有点复杂

五步走

1、确定dp数组含义

如果拿不准dp数组中的元素是什么类型，可以看看题目的示例返回的是什么类型的值，那一般就是需要找的值

这里题目要判定字典wordDict中的单词能不能拼成字符串s

那么实现过程中肯定要用字典wordDict中的单词与当前遍历区间内截取到的子串进行比较，要么相同要么不同，再结合示例的返回值，可以判断dp数组中的值应该是布尔类型

回到正题，dp数组究竟代表什么意思

假设有一个长度为i的字符串s的子串，若dp[i] = true

那么dp[i]表示该字符串可以拆分为1个或多个字典wordDict中的单词（可以理解为：dp[i]是对遍历过程中某个子串是否能拆分为wordDict中单词的一个认证，true就是能拆，false就是拆不了）

2+3、确定递推公式和初始化dp数组

这个递推公式的条件可太多了，为什么连起来一块说，看到后面就知道了

首先，因为我们要不断遍历字符串s并截取子串，通过查找子串是否存在于字典wordDict中来判断当前子串是否可以拆分

为什么要判断子串是否可以拆分？

因为一旦遍历完字符串s，那么此时的子串就是s本身了。进而就可以求s能不能被拆分为字典wordDict中的单词，这里体现了dp的思想，即前一轮遍历的子串会影响下一轮的，最终影响整个结果

所以，第一个条件是：所遍历区间内的子串必须出现在字典中

在说第二个条件之前，有必要说一下 "不断遍历字符串s并截取子串" 的实现方式

其实就是双指针

		for (int i = 1; i <= s.size(); i++) {   // 遍历背包

            for (int j = 0; j < i; j++) {       // 遍历物品

                string word = s.substr(j, i - j); //substr(起始位置，截取的个数)

                if (wordSet.find(word) != wordSet.end() && dp[j]) {//这里wordSet是一个unordered_set

                    dp[i] = true;

                }

            }

        }

下面用图来解释一下遍历过程

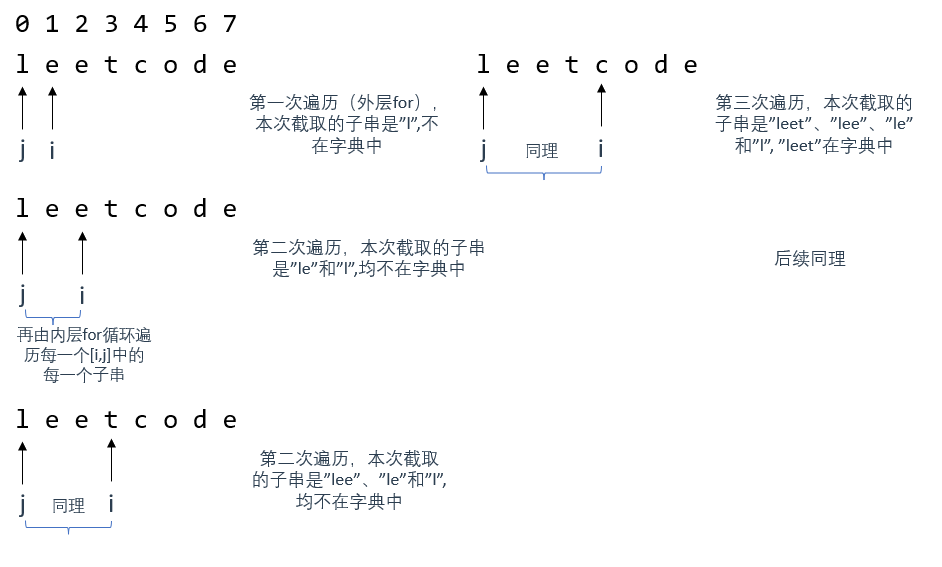
上图推导了两层for循环的遍历过程，其中，外层for循环负责遍历字符串s（也就是所谓的背包），而内层for则用来在[j,i]区间内遍历所有该区域内的子串，用来在wordSet中查询

如图所示，当外层for遍历到 i = 4 ，才获取到第一个能在wordSet中查询到的子串"leet"

为什么不是在i = 3时得到？因为substr函数截取子串的区间时左闭右开的，详见题外话

注意j遍历截取区间[j,i]内所有子串的顺序：它是先截最长的（如图所示）

此时，如果我们将dp[0]初始化为true

那么，每次i移动的时候，j重置为0，dp[j]就为true

若本次i移动到的位置，在j第一次获取子串时就能获取到目标子串的话，其实就找到了一个满足条件的子串

所以，此时的dp[i]也应该为true

因此，第二个条件就是：[j, i] 这个区间的子串是否出现在字典里

综上所述，本题的递推公式是： if([j, i] 这个区间的子串出现在字典里 && dp[j]是true) 那么 dp[i] = true。（j < i ）

初始化就是dp[0] = true（我认为完全是为了代码实现考虑，没有别的含义），其余位置是false

4、确定遍历顺序

因为题目说了，字符串s中可能会有"一个或多个"能够拆分为字典中单词的子串，也就是说背包中可以放多个相同的物品（单词），所以这是一个完全背包问题

而构成子串必须按一定顺序才能构成字符串s，所以本题的完全背包求的是排序（排列有序组合无序）（排列组合的区别详见）

所以遍历顺序是：先背包容量后物品

代码

太绕了，终于到代码了

class Solution {

public:

    bool wordBreak(string s, vector<string>& wordDict) {

        //定义dp数组

        vector<bool> dp(s.size() + 1, false);

        //初始化

        dp[0] = true;

        //遍历dp数组

        //先将wordDict放入一个unordered_set便于使用子串进行查找

        unordered_set<string> wordSet(wordDict.begin(), wordDict.end());

        for(int i = 1; i <= s.size(); ++i){//先遍历背包，字符串s

            for(int j = 0; j < i; ++j){//再遍历物品

                string word = s.substr(j, i - j);//使用j不断截取区间内的子串

                if(wordSet.find(word) != wordSet.end() && dp[j]) dp[i] = true;

            }

        }

        return dp[s.size()];

    }

};