大根堆的pop&remove&initialize

1. 定义

1. [max(min) tree] 一棵树, 其中每个节点的值都大于 (小于) 或等于其 children (如果有) 的值.
2. [max(min) heap] max(min) tree + complete binary tree.

2. 性质

1. heap 是一种 隐式数据结构 (implicit data structure).
   
   用 完全二叉树 表示的 heap 在数组中 隐式储存 (没有明确的指针或其他数据能够用来重塑这种结构).
   
   由于没有储存 结构信息, 这种表示方法的空间利用率很高 (没有浪费任何空间); 又由于用数组形式储存, 它的时间效率也很高.
2. 由于是 完全二叉树, 自然满足如下性质:
   1. 若一颗 complete binary tree 有 \(n\) 个元素, 那么它的高度为 \(\log_2 (n+1)\) .
   2. 设一颗 complete binary tree 中一元素的编号为 \(i\) , \(1 \leq i \leq n\) , 则有以下关系:
      • 若 \(i = 1\) , 则该元素为二叉树的 root; 若 \(i>1\) , 则其 parent 的编号为 \(\lceil i/2 \rceil\) .
      • 若 \(2i>n\) , 则该元素无 left child; 否则, 其 left child 的编号为 \(2i\) .
      • 若 \(2i+1>n\) , 则该元素无 right child; 否则, 其 right child 的编号为 \(2i+1\) .

3. 大根堆的 pop & remove

3.1. 核心逻辑 & 发现问题

不失一般性, 存在如下图一个大根堆.

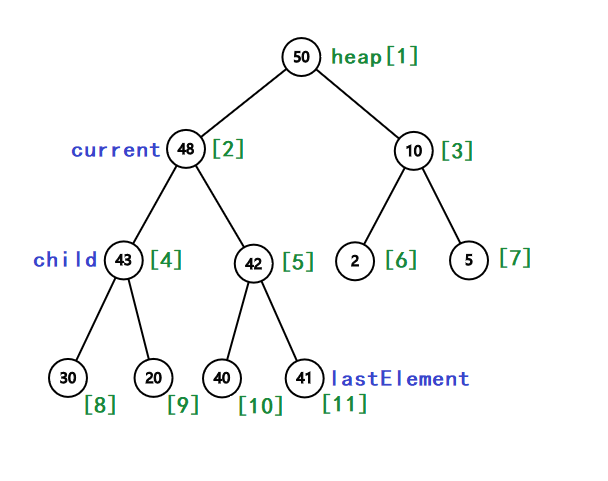
假设现在要删除 heap[current], 那么我们要做的核心步骤是:

• 将 heap[current] 的 children 中较大的那个 (我们假设那个结点是 heap[child] ) 移动到 heap[current] 的位置;

这时 heap[child] 相当于 "空" 的状态,

因此顺理成章地利用递归或迭代, 再把 heap[child] 当作新的 heap[current] 而反复执行核心步骤.

应当将 child 小于 heapSize 作为限制 iteration 或 recursion 继续进行的条件.

然而, 如果我们使用上述逻辑 pop 上图中的 heap[1]:

1. 48 填入 heap[1];
2. 43 填入 heap[2];
3. 30 填入 heap[4];
4. heap[8] 为空;

为满足 定义 1 和 定义 2, 此时若将 lastElement = 41 填入 heap[8], 则 heap[4] = 30 小于 heap[8] = 41, 与 定义 1 产生冲突.

为什么会出现这样的问题呢?

根据 定义 1:

[max(min) tree] 一棵树, 其中每个结点的值都大于(小于)或等于其 children (如果有)的值.

我们应该明确一点:

• 整体上, 大根树中下层元素不一定大于上层元素, 而只是每个结点要大于自己所有的 descendent.

如上图, 尽管 heap[11] 在 level 4; 但仍比处于 level 2 的 heap[3] 大.

这就是为什么在 pop 或者 remove 时, 我们需要更加复杂的方法进行 重构.

3.2. 重构大根堆

2.1. 提出的问题不建议使用 recursion 解决; 因为如果用 iteration, 只要在循环体中添加一步简单的判断就即可.

再次观察前文的大根堆:

我们发现, 冲突的产生本质上是因为,

尽管 heap[4] 是 silblings 中较大的那个, 但它的 child heap[8] 并没有其 sibling (也就是 heap[5]) 的 child heap[11] = lastElement 大.

那么, 我们只要在保持核心逻辑的同时, 一旦发现 heap[current] 的较大 child 比 lastElement 小, 那就结束循环, 把 lastElement 填入 heap[current]! 后面的就不用管了!

如果没找到......那就继续循环, 循环到底, 把 lastElement 填到最下面就好.

3.3. 代码实现

1. pop最顶端元素(root).

template<class T>
void maxHeap<T>::pop() {
    if (heapSize == 0) throw queueEmpty();
    // Delete the largest element.
    heap[1].~T();
    // Delete the last element and re-construct the heap.
    T lastElement = heap[heapSize];
    heap[heapSize--].~T();
    // Starting from the root, find location for the last element.
    int current = 1,
        child = 2;
    // Loop until the end.
    while (child <= heapSize) {
        // "child" should be the larger child of "current"
        if (child < heapSize && heap[child] < heap[child + 1]) { child++; }
        // IF: "current" points to a node whose child is smaller than "lastElement",
        // indicating that "lastElement" can be put in "heap[current]".
        if (lastElement >= heap[child]) {
            // End loop.
            break;
        }
        // OTHERWISE.
        else {
            heap[current] = heap[child];
            current = child;
            // Move "child" to its child.
            child << 1;
        }
    }
    heap[current] = lastElement;
}

1. remove下标为 i 的元素.

template<class T>
T maxHeap<T>::remove(int i) {
    if (heapSize == 0) throw queueEmpty;
    T theDeleted = heap[i];
    T lastElement = heap[heapSize];
    heap[heapSize].~T();
    int current = i, child = i << 1;
    while (child <= heapSize) {
        // Make sure "child" points to the larger one between the sublings.
        if (child < heapSize && heap[child] < heap[child + 1]) {
            child++;
        }
        // IF: "current" points to a node whose child is smaller than "lastElement",
        // indicating that "lastElement" can be put in "heap[current]".
        if (lastElement >= heap[child]) {
            // End loop.
            break;
        }
        // OTHERWISE.
        else {
            heap[current] = heap[child];
            current = child;
            child <<= 1;
        }
    }
    heap[current] = lastElement;
    return theDeleted;
}

3.4. 复杂度分析

对于方法 pop, 遍历只迭代至 left/right child, 因此时间复杂度为:

\[O(\log{n})
\]

方法 remove 的复杂度取决于目标 node 的 descendent 的数量.

4. Initialize

4.1. 逻辑分析

root 从最后一个 node 的 parent node 开始向根迭代, 直至 max heap 真正的根;

对于迭代中的每个 root, child 从其 child node 开始向 descendent 迭代 (迭代需要保证 child 指向 siblings 中较大的那个):

• 若 rootElement 小于 child 的元素, 则 child 继续向 descendent 迭代, 同时将 child 的元素覆盖至 child/2;
• 若 rootElement 大于等于 child 的元素, 则 child 终止迭代, 同时将 rootElement 存入 child/2;

4.2. 代码实现

template<class T>
void maxHeap<T>::initialize(T* theHeap, int theSize)
{
    delete[] heap; // Empty the memory of "T* maxHeap<T>::heap".
    heap = theHeap; // Make "heap" points to "theHeap".
    heapSize = theSize; // Set the "heapSize".

    // 'root' would iterates from {heapSize/2 (parent of the last element)} and keep decreasing until reaches real root.
    for (int root = heapSize / 2; root >= 1; root--) {
        // Pick up the current element of 'root'.
        T rootElement = heap[root];
        int child = 2 * root;
        // 'child' iterates from the child of current root to end, but cannot be larger than 'heapSize'.
        for (; child <= heapSize; child *= 2) {
            // Ensure 'heap[child]' is the larger one between the siblings.
            if (child < heapSize && heap[child] < heap[child + 1]) { child++; }
            if (rootElement >= heap[child]) { // IF: 'rootElement' can be put in 'heap[child/2]'.
                break;
            }
            // IF: "rootElement" cannot be put in "heap[child/2]".
            // Move 'heap[child]' to 'heap[child/2]'.
            heap[child/2] = heap[child];
            // Re-allocate the next level to 'child'.
        }
        heap[child / 2] = rootElement;
    }
}

4.3. Complexity

假设元素个数为 \(n\), 高度为 \(h\).

• 由于外层 for 循环 root 从 \(n/2\) 开始迭代, 因此从元素上看总共迭代了 \(n/2\) 次, 从层数上看总共迭代了 \(h-1\) 层.
• 内层 for 循环的每次迭代, 实际上都遍历了一棵 complete binary tree, 复杂度为 \(O(h_{i})\). 其中 \(h_{i}\) 是该层 complete binary tree 的高度.
• binary tree 的第 \(j\) 层, 最多有 \(2^{j-1}\) 个 node; 而每个 node 的高度 \(h_{i}=h-j+1\).

\[O(\sum_{j=1}^{h-1}{2^{j-1}(h-j+1)}) = O(\sum_{k=2}^{h}{2^{h-k}k})=O(2^h\sum_{k=2}^{h}{\frac{k}{2^k}})=O(2^h)
\]

因为有 \(n\) 个元素的 complete binary tree 的高度为 \(h= \lceil \log_{2}{(n+1)} \rceil\), 因此:

\[O(2^h)=O(2^{\lceil \log_{2}{(n+1)} \rceil})=O(n)
\]

由于外层 for 循环从元素上看迭代了 \(n/2\) 次, 所以复杂度下限为 \(\Omega(n)\).

综上, 方法 initialize 的复杂度为:

\[\Theta(n)
\]

---

Reference | Data Structures, Algoritms, and Applications in C++, Sartaj Sahni