常见算法的时间复杂度（大O计数法）

定义

​ 对于不同的机器环境而言，确切的单位时间是不同的，但是对于算法进行多少个基本操作（即花费多少时间单位）在规模数量级上却是相同的，由此可以忽略机器环境的影响而客观的反应算法的时间效率。

对于算法的时间复杂度效率，我们可以用“大O记法”来表示。

“大O记法”：对于单调的整数函数f，如果存在一个整数函数g和实常数c>0，使得对于充分大的n总有f(n)<=c*g(n)，就说函数g是f的一个渐近函数（忽略常数），记为f(n)=O(g(n))。也就是说，在趋向无穷的极限意义下，函数f的增长速度受到函数g的约束，亦即函数f与函数g的特征相似。

时间复杂度：假设存在函数g，使得算法A处理规模为n的问题示例，所用时间为T(n)=O(g(n))，

    对于算法进行特别具体的细致分析虽然很好，但在实践中的实际价值有限。对于算法的时间性质和空间性质，最重要的是其数量级和趋势，这些是分析算法效率的主要部分。而计量算法基本操作数量的规模函数中那些常量因子可以忽略不计。例如，可以认为3n^2和100n^2属于同一个量级，如果两个算法处理同样规模实例的代价分别为这两个函数，就认为它们的效率“差不多”，都为n^2级。

• 我们主要关注算法的最坏情况，亦即最坏时间复杂度。

基本计算规则

1、基本操作，即只有常数项，认为其时间复杂度为O(1)
2、顺序结构，时间复杂度按加法进行计算
3、循环结构，时间复杂度按乘法进行计算
4、分支结构，时间复杂度取最大值
5、判断一个算法的效率时，往往只需要关注操作数量的最高次项，其它次要项和常数项可以忽略
6、在没有特殊说明时，我们所分析的算法的时间复杂度都是指最坏时间复杂度

常见时间复杂度

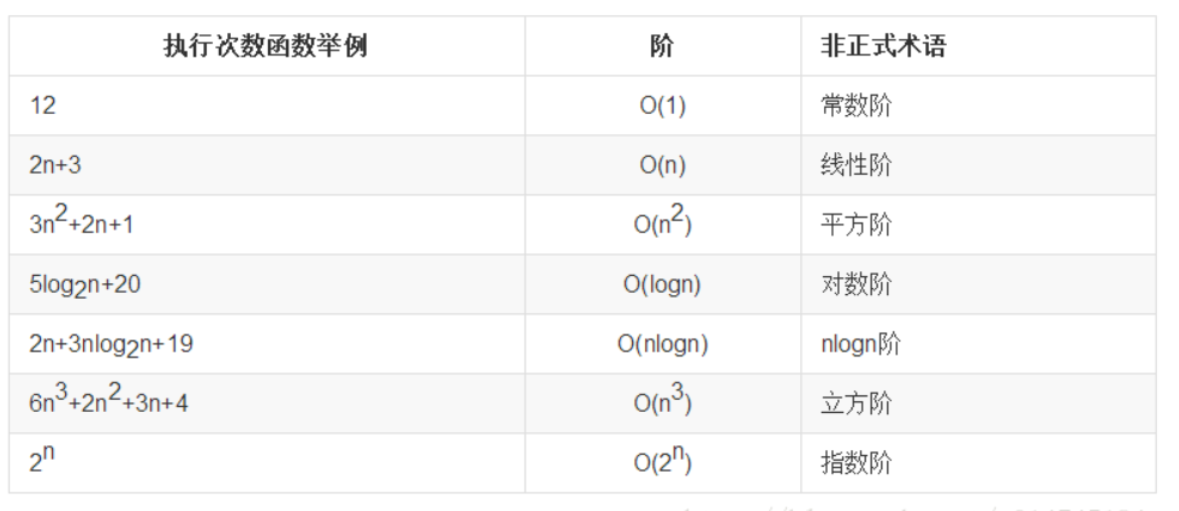
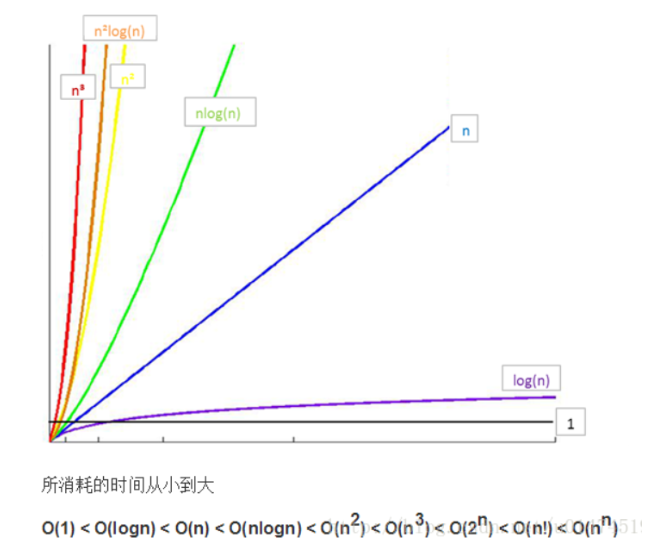
常见时间复杂度之间的关系

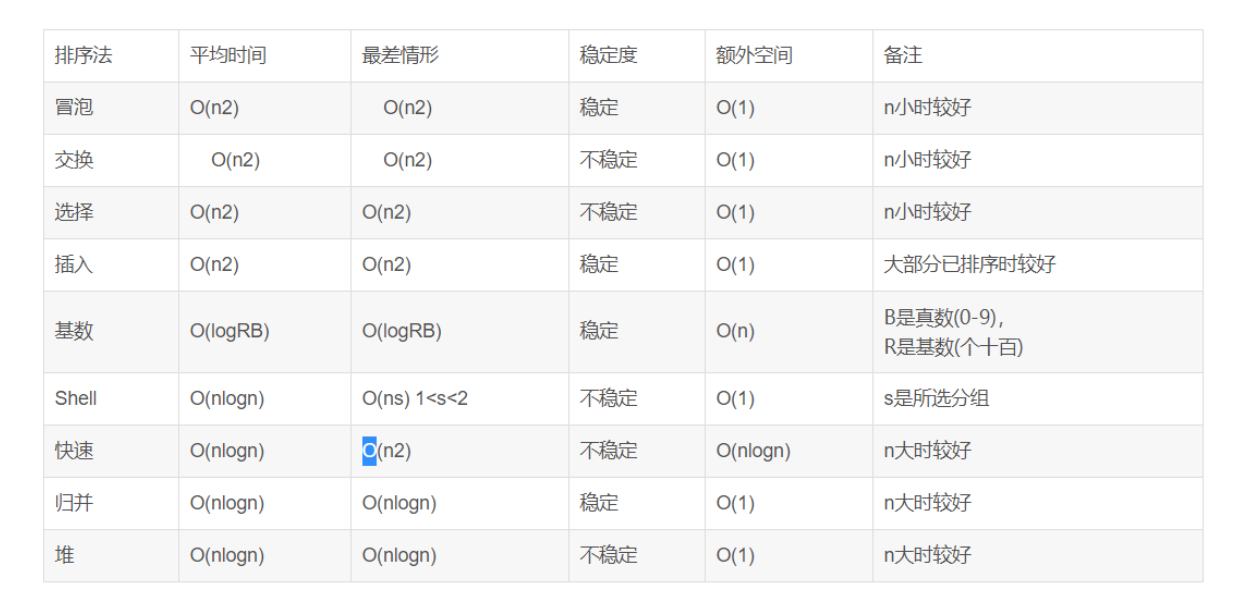
排序算法的时间复杂度