B+树索引页大小是如何确定的？

B+树简介

在正式介绍本文的主题前，需要对 B+ 树有一定的了解，B+树是一种磁盘上数据的索引结构，大概长这个样子。

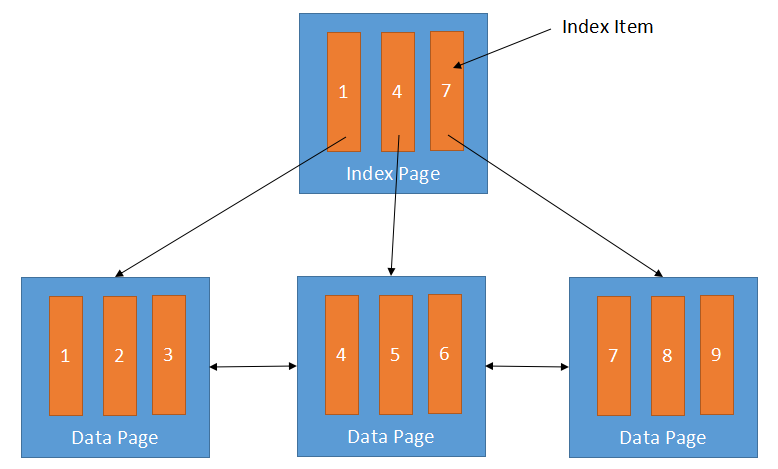
B+树的叶子节点是所有的数据，非叶子节点称为索引页，索引页里有若干个索引项，本例中有 3 个索引项，也就是索引页的出度为 3，表示它有 3 个子节点。

相要寻找某一个数据时，比如值为 6 的数据，只需要先在索引页中找到小于 6 的最大的索引项 4，就可以索引到保存了 4，5，6 三条数据的数据页，进而找到值为 6 的这一条数据。

当然，B+ 树不是只有一个索引节点，只是为了方便展示所以图中只有一个索引节点，一个更大的 B+ 树如下图所示。

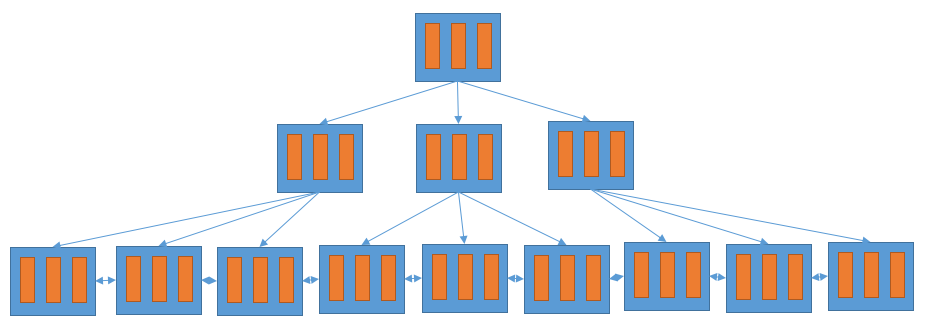
数学推导

假设 B+ 树总共索引了 N 条数据（叶子节点的数据量），每个索引页的出度为 EntriesPerPage（索引页内有多少个索引项），则 B+ 树的高度可以由如下式子计算：

\[IndexHeight \approx \frac{log_{2}{N}}{log_{2}{EntriesPerPage}}
\]

定义 IndexPageUtility 为衡量索引页到数据页的远近的指标，可以由如下式子计算：

\[IndexPageUtility = log_{2}{EntriesPerPage}
\]

这里可以不必纠结为什么 utility 就是这么算的，只要理解 utility 和 EntriesPerPage 是正相关的关系就可以，因为最后算的收益成本比率只是一个比值，能比较出大小就可以，所以这里就取 utility 为 IndexHeight 计算公式的分母。

举个例子，如果索引项大小为 20 字节，那么 2KB 的索引页应该是能装下 100 个索引项，但实际上索引页内不仅仅只存有索引项，实际索引项最高能占用 70% 的空间，也就是 70 个索引项。这样的索引页的 utility 为 \(log_{2}{70}\) 约为 6.2，大约是 128KB 大小索引页 utility 的一半。

每一次读索引页都需要读一次磁盘，相应的距离目标数据也更进一步（使用 utility 衡量步长）。基于这种成本效益的权衡，产生了一个最佳的页面大小，平衡了读一次索引页的收益（IndexPageUtility）和成本（IndexPageAccessCost）。

对于越大的索引页，它的出度越大，utility 越高，从磁盘读取的成本也越高，对于特定的磁盘的寻址时间和传输速率，有一个最优的索引页大小。

假设磁盘平均寻址时间为 10 毫秒，传输速率为 10MB 每秒，索引页大小为 2KB，那么读取索引页需要的时间为 10.2 毫秒。

更准确的说，读取索引页的成本要么是有页面缓存时的内存存储成本，要么是从磁盘读取页面的磁盘访问成本。如果根索引页及附近的索引页缓存在内存中，能够节省一个数量恒定的 IO 次数，这个数量一般是可以忽略的。

因此从磁盘读取索引页的成本可以由如下式子计算，DiskLatency 为磁盘寻址时间。

\[IndexPageAccessCost = DiskLatency + \frac{PageSize}{DiskTransferRate}
\]

那么读取索引页的收益和成本的比率就是：

\[BenefitCostRatio = \frac{IndexPageUtility}{IndexPageAccessCost}
\]

应用分析

假设磁盘平均寻址时间为 10 毫秒，传输速率为 10MB 每秒，索引项大小为 20 字节，下表给出不同索引页大小对应的收益成本比率。

IndexPageSize(KB)	EntriesPerPage	IndexPageUtility	IndexPageAccessCost	BenefitCostRatio
2	68	6.1	10.2	0.60
4	135	7.1	10.4	0.68
8	270	8.1	10.8	0.75
16	541	9.1	11.6	0.78
32	1081	10.1	13.2	0.76
64	2163	11.1	16.4	0.68
128	4325	12.1	22.8	0.53

通过上表可以得出，索引页大小在 8KB 到 32KB 是收益成本比率是最优的。索引页过小或过大都不是好的选择。且该索引页大小范围也随着磁盘传输速率的提升而发生变化，当传输速率为 40MB 每秒，最优的索引页大小将变成 32KB 到 128 KB。