cf 450c Jzzhu and Chocolate
1 second
256 megabytes
standard input
standard output
Jzzhu has a big rectangular chocolate bar that consists of n × m unit squares. He wants to cut this bar exactly k times. Each cut must meet the following requirements:
- each cut should be straight (horizontal or vertical);
- each cut should go along edges of unit squares (it is prohibited to divide any unit chocolate square with cut);
- each cut should go inside the whole chocolate bar, and all cuts must be distinct.
The picture below shows a possible way to cut a 5 × 6 chocolate for 5 times.
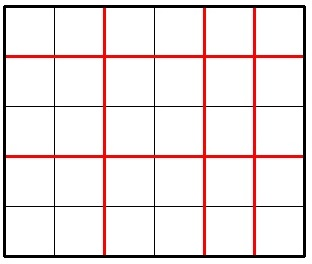
Imagine Jzzhu have made k cuts and the big chocolate is splitted into several pieces. Consider the smallest (by area) piece of the chocolate, Jzzhu wants this piece to be as large as possible. What is the maximum possible area of smallest piece he can get with exactly k cuts? The area of a chocolate piece is the number of unit squares in it.
A single line contains three integers n, m, k (1 ≤ n, m ≤ 109; 1 ≤ k ≤ 2·109).
Output a single integer representing the answer. If it is impossible to cut the big chocolate k times, print -1.
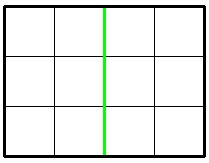
3 4 1
6
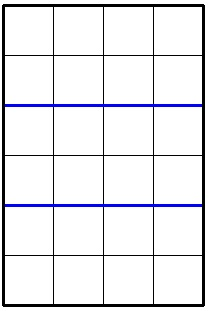
6 4 2
8
2 3 4
-1
In the first sample, Jzzhu can cut the chocolate following the picture below:
In the second sample the optimal division looks like this:
In the third sample, it's impossible to cut a 2 × 3 chocolate 4 times.
#include<iostream>
#include<stdio.h>
using namespace std;
int main()
{
long long n,m,k;
while(~scanf("%I64d%I64d%I64d",&n,&m,&k))
{
if(n>=k+||m>=k+)
{
long long maxx=max(n,m);
long long minn=min(n,m);
long long cl1=minn/(+k);
long long cl2=maxx/(+k);
//cout<<minn<<endl<<maxx<<endl<<cl1<<endl<<cl2<<endl;
long long tmpma=;
long long tmpmi=;
tmpmi=maxx*cl1;
tmpma=minn*cl2;
long long ans=max(tmpmi,tmpma);
if(ans>) printf("%I64d\n",ans);
//printf("%I64d\n",maxx/(k+1)*minn);
continue;
}
long long minn=min(n,m);
long long maxx=max(n,m);
long long cl1=k-minn+;
long long cl2=k-maxx+;
//cout<<minn<<endl<<maxx<<endl<<cl1<<endl<<cl2<<endl;
long long tmpma=;
long long tmpmi=;
if(cl1<maxx) tmpmi=maxx/(cl1+);
if(cl2<minn) tmpma=minn/(cl2+);
long long ans=max(tmpmi,tmpma);
if(ans>) printf("%I64d\n",ans);
else printf("-1\n");
}
return ;
}//
我感觉这道题是一种很巧妙的暴力,枚举可能的四种情况,取最大值。
cf 450c Jzzhu and Chocolate的更多相关文章
- codeforces 450C. Jzzhu and Chocolate 解题报告(449A)
题目链接:http://codeforces.com/contest/450/problem/C 题目意思:给出一个 n * m 大小的chocolate bar,你需要在这个bar上切 k 刀,使得 ...
- Codeforces 450C:Jzzhu and Chocolate(贪心)
C. Jzzhu and Chocolate time limit per test: 1 seconds memory limit per test: 256 megabytes input: st ...
- Codeforces Round #257 (Div. 1)449A - Jzzhu and Chocolate(贪婪、数学)
主题链接:http://codeforces.com/problemset/problem/449/A ------------------------------------------------ ...
- CF 633 F. The Chocolate Spree 树形dp
题目链接 CF 633 F. The Chocolate Spree 题解 维护子数答案 子数直径 子数最远点 单子数最长直径 (最长的 最远点+一条链) 讨论转移 代码 #include<ve ...
- Codeforces Round #257 (Div. 2) C. Jzzhu and Chocolate
C. Jzzhu and Chocolate time limit per test 1 second memory limit per test 256 megabytes input standa ...
- Codeforces449A Jzzhu and Chocolate && 449B Jzzhu and Cities
CF挂0了,简直碉堡了.两道题都是正确的思路但是写残了.写个解题报告记录一下心路历程. A题问的是 一个n*m的方块的矩形上切k刀,最小的那一块最大可以是多少.不难发现如果纵向切k1刀,横向切k2刀, ...
- Jzzhu and Chocolate
CF#257 div2 C:http://codeforces.com/contest/450/problem/C 题意:n*m的方格,每次可以横着或者纵向的切一刀,问切k之后,最小的最大是多少. 题 ...
- codeforces #257 C称号Jzzhu and Chocolate
职务地址:http://codeforces.com/contest/450/problem/C 这次CF的时候绝壁脑残了. ..A题和C题都出现了脑残失误... 唯一一个AC的B题还是被HACK了. ...
- CF 450E Jzzhu and Apples 数学+模拟
E. Jzzhu and Apples time limit per test 1 second memory limit per test 256 megabytes input standard ...
随机推荐
- Tensorflow 之 name/variable_scope 变量管理
name/variable_scope 的作用 充分理解 name / variable_scope TensorFlow 入门笔记 当一个神经网络比较复杂.参数比较多时,就比较需要一个比较好的方式来 ...
- Web开发中的6个坏习惯
在 Usersnap,我们在能很好的组织网站开发有超过20(总和)年的经验.我们认为这些过去的经验能让我们很好的分辨出什么是好.坏和丑陋的网站开发.如今我们不想把注意力放在消极的部分,但就这一次,我们 ...
- 使用dulilib DirectUI库(一)
1.在创建的窗口类里面 需要继承CWindowWnd.INotifyUI 对于CWindowWnd里面的方法: 实现;,重载virtualUINTGetClassStyle()const;返回窗口的风 ...
- @Autowired注入了dao,为什么还要写getDao(){return userDao}这个方法?有什么作用?
Autowired private UserDao userDao; @Override public BaseDao<User> getDao() { return userDao; } ...
- DevExpressComponents-14.2.5 破解过程,正在编写,未完
首先,批评一下cnblogs,在win10的环境下,需要加入到兼容视图列表方可正常编辑内容, 声明,本人在14.2.3 的源代码环境下,编译未通过,相关功能报错,索性选择破解,在此,只是学习测试使用, ...
- (剑指Offer)面试题48:不能被继承的类
题目: 写一个不能被继承的类 思路: 1.把构造函数设为私有函数 在C++中子类的构造函数会自动调用父类的构造函数,子类的析构函数也会自动调用父类的构造函数,要想一个类不能被继承,只要把它的构造函数和 ...
- Java打包生成exe(使用exe4j和inno setup)
Java打包生成exe 生成jar 先使用eclipse生成可执行的jar[可执行的jar包含内容更全面,包括指定主类的.mf] Exe4j的使用 一定要可执行jar进行打包. Project typ ...
- 手动脱UPX 壳实战
作者:Fly2015 Windows平台的加壳软件还是比較多的,因此有非常多人对于PC软件的脱壳乐此不彼,本人菜鸟一枚,也学习一下PC的脱壳.要对软件进行脱壳.首先第一步就是 查壳.然后才是 脱壳. ...
- NGUI Tutorial 4 ScrollView
一.createScrollView 1.First, select the panel you want to be your scroll view and right-click anywher ...
- 算法笔记_146:TarJan算法的应用(Java)
目录 1 问题描述 2 解决方案 1 问题描述 Problem Description 为了训练小希的方向感,Gardon建立了一座大城堡,里面有N个房间(N<=10000)和M条通道(M& ...
