Codeforces 1131 F. Asya And Kittens-双向链表(模拟或者STL list)+并查集(或者STL list的splice()函数)-对不起，我太菜了。。。 (Codeforces Round #541 (Div. 2))

F. Asya And Kittens

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Asya loves animals very much. Recently, she purchased nn kittens, enumerated them from 11 and nn and then put them into the cage. The cage consists of one row of nn cells, enumerated with integers from 11 to nn from left to right. Adjacent cells had a partially transparent partition wall between them, hence there were n−1n−1 partitions originally. Initially, each cell contained exactly one kitten with some number.

Observing the kittens, Asya noticed, that they are very friendly and often a pair of kittens in neighboring cells wants to play together. So Asya started to remove partitions between neighboring cells. In particular, on the day ii, Asya:

• Noticed, that the kittens xixi and yiyi, located in neighboring cells want to play together.
• Removed the partition between these two cells, efficiently creating a single cell, having all kittens from two original cells.

Since Asya has never putted partitions back, after n−1n−1 days the cage contained a single cell, having all kittens.

For every day, Asya remembers numbers of kittens xixi and yiyi, who wanted to play together, however she doesn't remember how she placed kittens in the cage in the beginning. Please help her and find any possible initial arrangement of the kittens into nn cells.

Input

The first line contains a single integer nn (2≤n≤1500002≤n≤150000) — the number of kittens.

Each of the following n−1n−1 lines contains integers xixi and yiyi (1≤xi,yi≤n1≤xi,yi≤n, xi≠yixi≠yi) — indices of kittens, which got together due to the border removal on the corresponding day.

It's guaranteed, that the kittens xixi and yiyi were in the different cells before this day.

Output

For every cell from 11 to nn print a single integer — the index of the kitten from 11 to nn, who was originally in it.

All printed integers must be distinct.

It's guaranteed, that there is at least one answer possible. In case there are multiple possible answers, print any of them.

Example

input

Copy

5
1 4
2 5
3 1
4 5

output

Copy

3 1 4 2 5

Note

The answer for the example contains one of several possible initial arrangements of the kittens.

The picture below shows how the cells were united for this initial arrangement. Note, that the kittens who wanted to play together on each day were indeed in adjacent cells.

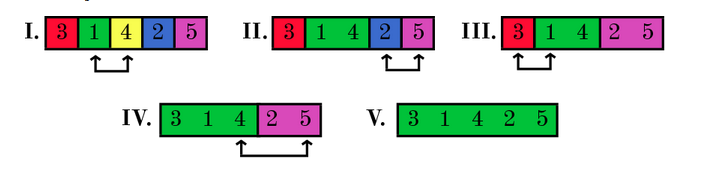
题意就是给你两个数合并的顺序让你构造序列。

一开始没想起来，以为是单链表，突然想到要有前驱，就想到双向链表了，但是一直卡D，没时间了，这是一个过的比D多的F题。。。

思路就是双向链表+并查集，具体的代码写了注释。

两种代码，一个是模拟的双向链表+并查集，一个是用STL的list+list的splice()函数。

看的某大佬群里大佬的代码。

代码一：

 //F-双向链表(模拟)+并查集
 #include<bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 const int maxn=*1e5+;

 int l[maxn],r[maxn],nex[maxn],root[maxn];

 int findr(int x)//递归并查集
 {
     if(root[x]==x) return x;
     return root[x]=findr(root[x]);
 }

 int main()
 {
     int n,u,v;
     cin>>n;
     for(int i=;i<=n;i++)
         root[i]=l[i]=r[i]=i;//初始化
     while(n>){
         n--;
         cin>>u>>v;
         u=findr(u);
         v=findr(v);
         root[v]=u;//并查集合并
         nex[r[u]]=l[v];//当前u的最右端的节点与v的最左端的节点相连
         r[u]=r[v];//将u的最右端节点更新为v的最右端节点
     }
     u=l[findr()];//找到头节点
     while(u){
         cout<<u<<" ";
         u=nex[u];//按照连接顺序输出
     }
 }

代码二:

 //F-STL list(双向链表)+list拼接合并 splice函数(实现并查集的操作)
 /*
 list的splice函数主要是用来合并两个list
 splice函数是list中特有的拼接方式，splice实现了不需要拷贝的list合并，
 即可以在常数时间内从list的一个区域拼接到另一个list的一个区域。
 也就是说splice是一个常数时间的函数（但是也会产生其他形如list的size()问题，导致size()处理时间为O(n)不为常数)
 l1.splice(l1.begin(),it);//(要插入的位置迭代器，要插入的元素的迭代器）
 */
 #include<bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 const int maxn=*1e5+;

 int fa[maxn];

 int find(int x)//递归并查集
 {
     return x==fa[x]?x:fa[x]=find(fa[x]);
 }

 list<int> h[maxn];

 int main()
 {
     int n;
     cin>>n;
     for(int i=;i<=n;i++){//初始化，一开始各个list里面只有自己，父节点就是自己
         h[i].push_back(i);
         fa[i]=i;
     }
     for(int i=;i<n;i++){
         int x,y;
         cin>>x>>y;
         x=find(x);
         y=find(y);
         fa[y]=x;//并查集节点合并
         h[x].splice(h[x].end(),h[y]);//在h[x]的尾部插入h[y]
     }
     for(auto it:h[find()]){
         cout<<it<<" ";
     }
     cout<<endl;
 }

想晚了，对不起，比赛的时候没出来这道题。。。