最小二乘法 及 梯度下降法 分别对存在多重共线性数据集 进行线性回归 （Python版）

网上对于线性回归的讲解已经很多，这里不再对此概念进行重复，本博客是作者在听吴恩达ML课程时候偶然突发想法，做了两个小实验，第一个实验是采用最小二乘法对数据进行拟合， 第二个实验是采用梯度下降方法对数据集进行线性拟合，下面上代码：

最小二乘法：

#!/usr/bin/env python
#encoding:UTF-8
import numpy as np
import matplotlib.pyplot as plt

N=10
X=np.linspace(-3, 3, N)
Y=(X+10.0)/2.0
Z=-5.0+X+3.0*Y 

P=np.ones((N, 1))
P=np.c_[P, X, Y]

t=np.linalg.pinv(P)
w=np.dot(t, Z)

print "拟合后的权重："
print w
A=np.dot(P, w)-Z

print "拟合后的LOSTFUNCTION值："
print np.dot(A, A)/2

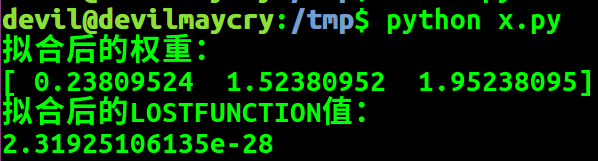
由LOSTFUNCTION值可知所得权重可以使得模型得到较少的损失。

由代码中给出的拟合权重和代码运行后得出的拟合权重可以很清楚的发现并不一致，由此很容易得出该数据集对于线性模型存在多重共线性。

梯度下降法：

#!/usr/bin/env python
#encoding:UTF-8
import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)

N=10

X=np.linspace(-3, 3, N)
Y=(X+10)/2
Z=-5+X+3*Y

P=np.ones((N, 1))
P=np.c_[P, X, Y]

alafa=0.001

def fun():
    W=np.random.random(3)

    for _ in xrange(1000000000):
        A=(np.dot(P, W)-Z)

        W0=alafa*( np.sum(A) )
        W1=alafa*( np.dot(A, X) )
        W2=alafa*( np.dot(A, Y) )

        if abs(W0)+abs(W1)+abs(W2)<0.000001:
            break

        W[0]=W[0]-W0
        W[1]=W[1]-W1
        W[2]=W[2]-W2 

    return W

list_global=[]
for _ in xrange(100):
    list_global.append( fun() )
list_global.sort(key=lambda x:x[0])
for k in list_global:
    print k

运行结果：

devil@devilmaycry:/tmp$ python x2.py
[ 0.13859798  1.51383611  1.97228226]
[ 0.15812746  1.51578866  1.9683764 ]
[ 0.15935113  1.51591164  1.96813162]
[ 0.16440946  1.51641705  1.96711998]
[ 0.20540823  1.52051731  1.9589202 ]
[ 0.25569366  1.52554514  1.94886317]
[ 0.25880876  1.52585729  1.9482401 ]
[ 0.27499425  1.52747539  1.94500304]
[ 0.27534702  1.52751115  1.94493244]
[ 0.27945902  1.52792177  1.94411009]
[ 0.28400393  1.52837623  1.94320111]
[ 0.28696386  1.52867268  1.94260909]
[ 0.30536768  1.53051274  1.93892835]
[ 0.31818944  1.53179514  1.93636398]
[ 0.32798936  1.53277487  1.93440402]
[ 0.33334942  1.53331098  1.933332  ]
[ 0.34418953  1.53439535  1.93116395]
[ 0.3463948   1.53461533  1.93072294]
[ 0.3567094   1.53564731  1.92865998]
[ 0.36449799  1.53642554  1.92710231]
[ 0.38157383  1.53813337  1.92368712]
[ 0.38437965  1.53841409  1.92312594]
[ 0.40486422  1.54046214  1.91902906]
[ 0.41061448  1.54103779  1.91787896]
[ 0.43215718  1.54319227  1.91357041]
[ 0.43668932  1.54364513  1.912664  ]
[ 0.45612785  1.54558868  1.90877632]
[ 0.45977762  1.54595351  1.90804638]
[ 0.464536    1.54643     1.90709465]
[ 0.4673361   1.54670955  1.90653467]
[ 0.47087532  1.54706372  1.9058268 ]
[ 0.47690637  1.54766664  1.90462061]
[ 0.47718128  1.54769405  1.90456563]
[ 0.48571646  1.54854761  1.90285859]
[ 0.49155064  1.5491312   1.90169175]
[ 0.50684386  1.55066075  1.89863308]
[ 0.53314394  1.55329031  1.8933731 ]
[ 0.53925928  1.55390247  1.89214999]
[ 0.55049834  1.55502603  1.8899022 ]
[ 0.55622356  1.55559837  1.88875717]
[ 0.55765135  1.55574137  1.8884716 ]
[ 0.57794078  1.55777008  1.88441373]
[ 0.57995539  1.55797184  1.88401078]
[ 0.59427067  1.55940304  1.88114775]
[ 0.64070329  1.56404638  1.87186122]
[ 0.66360817  1.56633707  1.86728023]
[ 0.66533542  1.56650939  1.86693481]
[ 0.67435485  1.56741169  1.8651309 ]
[ 0.67461209  1.56743719  1.86507947]
[ 0.67841117  1.56781728  1.86431964]
[ 0.70004027  1.56998004  1.85999383]
[ 0.70249948  1.57022613  1.85950197]
[ 0.70332716  1.57030915  1.85933642]
[ 0.71017421  1.57099365  1.85796702]
[ 0.71407859  1.57138402  1.85718615]
[ 0.7277948   1.57275571  1.85444291]
[ 0.72946533  1.57292232  1.85410883]
[ 0.73050737  1.57302649  1.85390043]
[ 0.73111226  1.57308748  1.85377941]
[ 0.73420373  1.5733964   1.85316114]
[ 0.74375506  1.57435197  1.85125084]
[ 0.76167277  1.57614361  1.8476673 ]
[ 0.76645953  1.5766221   1.84670997]
[ 0.77628556  1.57760457  1.84474477]
[ 0.78124114  1.5780999   1.84375367]
[ 0.79445023  1.57942128  1.84111182]
[ 0.82246882  1.58222329  1.83550809]
[ 0.83844516  1.58382098  1.83231282]
[ 0.8504276   1.58501882  1.82991636]
[ 0.85371404  1.58534781  1.82925904]
[ 0.86614329  1.58659024  1.82677323]
[ 0.86963538  1.58693955  1.82607481]
[ 0.87227961  1.58720441  1.82554593]
[ 0.87565432  1.58754174  1.824871  ]
[ 0.88307665  1.58828406  1.82338652]
[ 0.89447944  1.58942419  1.82110598]
[ 0.89722723  1.58969873  1.82055644]
[ 0.90304827  1.5902811   1.81939221]
[ 0.91298315  1.59127442  1.81740525]
[ 0.92325648  1.59230144  1.8153506 ]
[ 0.93695625  1.59367157  1.81261064]
[ 0.94954532  1.59493075  1.8100928 ]
[ 0.96887547  1.59686409  1.80622675]
[ 0.97346265  1.59732198  1.80530938]
[ 0.98253813  1.59822971  1.80349427]
[ 0.98361444  1.59833731  1.80327901]
[ 0.98569708  1.59854557  1.80286248]
[ 0.99156202  1.59913215  1.80168948]
[ 0.99512314  1.59948855  1.80097724]
[ 1.05384788  1.60536059  1.78923232]
[ 1.05416379  1.60539244  1.78916912]
[ 1.07563405  1.60753962  1.78487506]
[ 1.08513878  1.60848968  1.78297414]
[ 1.09067723  1.60904425  1.7818664 ]
[ 1.10849918  1.61082595  1.77830205]
[ 1.13617915  1.61359433  1.77276602]
[ 1.16159108  1.61613499  1.76768368]
[ 1.16994446  1.61697081  1.76601296]
[ 1.18300731  1.61827712  1.76340039]
[ 1.18811107  1.61878732  1.76237965]

由梯度下降法可知，对于存在多重共线性的数据集合进行线性拟合所得到的权重值并不一致，该权重值会随着初始权重值的不同而不同，该现象用一句比较学术的话来描述就是对初始状态敏感。