[ACM] hdu 1025 Constructing Roads In JGShining's Kingdom （最长递增子序列，lower_bound使用）

Constructing Roads In JGShining's Kingdom

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)

Total Submission(s): 14635    Accepted Submission(s): 4158

Problem Description

JGShining's kingdom consists of 2n(n is no more than 500,000) small cities which are located in two parallel lines.



Half of these cities are rich in resource (we call them rich cities) while the others are short of resource (we call them poor cities). Each poor city is short of exactly one kind of resource and also each rich city is rich in exactly one kind of resource.
You may assume no two poor cities are short of one same kind of resource and no two rich cities are rich in one same kind of resource. 



With the development of industry, poor cities wanna import resource from rich ones. The roads existed are so small that they're unable to ensure the heavy trucks, so new roads should be built. The poor cities strongly BS each other, so are the rich ones. Poor
cities don't wanna build a road with other poor ones, and rich ones also can't abide sharing an end of road with other rich ones. Because of economic benefit, any rich city will be willing to export resource to any poor one.



Rich citis marked from 1 to n are located in Line I and poor ones marked from 1 to n are located in Line II. 



The location of Rich City 1 is on the left of all other cities, Rich City 2 is on the left of all other cities excluding Rich City 1, Rich City 3 is on the right of Rich City 1 and Rich City 2 but on the left of all other cities ... And so as the poor ones. 



But as you know, two crossed roads may cause a lot of traffic accident so JGShining has established a law to forbid constructing crossed roads.



For example, the roads in Figure I are forbidden.








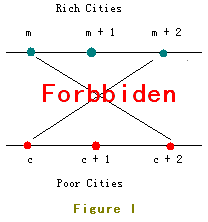
In order to build as many roads as possible, the young and handsome king of the kingdom - JGShining needs your help, please help him. ^_^

 

Input

Each test case will begin with a line containing an integer n(1 ≤ n ≤ 500,000). Then n lines follow. Each line contains two integers p and r which represents that Poor City p needs to import resources from Rich City r. Process to
the end of file.

 

Output

For each test case, output the result in the form of sample. 

You should tell JGShining what's the maximal number of road(s) can be built. 

 

Sample Input

2
1 2
2 1
3
1 2
2 3
3 1

 

Sample Output

Case 1:
My king, at most 1 road can be built.

Case 2:
My king, at most 2 roads can be built.

Hint

Huge input, scanf is recommended.
 
 
解题思路：

这题用来练lower_bound函数的使用。

这个函数从已排好序的序列a中利用二分搜索找出指向ai>=k的ai的最小的指针。类似的函数含有upper_bound，这一函数求出的是指向ai>k的ai的最小的指针。有了它们，比如长度为n的有序数组a中的k的个数，可以这样求出

upper_bound(a,a+n,k) - lower_bound(a,a+n,k)；

参考资料：http://www.cnblogs.com/cobbliu/archive/2012/05/21/2512249.html

代码：

#include <iostream>
#include <stdio.h>
#include <algorithm>
#include <string.h>
using namespace std;
//int dp[20];
const int inf=0x7fffffff;
//int a[7]={2,1,3,4,8,5,9};
const int maxn=500005;
int road[maxn];
int dp[maxn];

int main()
{
    /*fill(dp,dp+7,inf);
    for(int i=0;i<7;i++)
        cout<<dp[i]<<endl;
    for(int i=0;i<7;i++)
    {
        *lower_bound(dp,dp+7,a[i])=a[i];
    }
    int len=lower_bound(dp,dp+7,inf)-dp;
    for(int i=0;i<len;i++)
        cout<<dp[i]<<endl;*/
    int n;
    int from,to;
    int c=1;
    while(scanf("%d",&n)!=EOF)
    {

        fill(dp,dp+n,inf);
        for(int i=0;i<n;i++)
        {
            scanf("%d%d",&from,&to);
            road[from]=to;
        }
        for(int i=1;i<=n;i++)//因为题目输入的原因,这里的下标从1开始。
            *lower_bound(dp,dp+n,road[i])=road[i];
        int len=lower_bound(dp,dp+n,inf)-dp;
        if(len==1)
        {
            cout<<"Case "<<c++<<":"<<endl;
            cout<<"My king, at most 1 road can be built."<<endl;
        }
        else
        {
            cout<<"Case "<<c++<<":"<<endl;
            cout<<"My king, at most "<<len<<" roads can be built."<<endl;
        }
        cout<<endl;
    }
    return 0;
}

附上最长上升子序列的模板：

#include <iostream>
#include <stdio.h>
#include <algorithm>
#include <string.h>
using namespace std;
int dp[20];
const int inf=0x7fffffff;
int a[7]={2,1,3,4,8,5,9};
const int maxn=500005;
int main()
{
    fill(dp,dp+7,inf);
    for(int i=0;i<7;i++)
    {
        *lower_bound(dp,dp+7,a[i])=a[i];
    }
    int len=lower_bound(dp,dp+7,inf)-dp;
    for(int i=0;i<len;i++)
        cout<<dp[i]<<endl;
    return 0;
}