FWT公式一览
总表
| 真值表 | 对应运算 | FWT | IFWT | ||||
| A=B=0 | A≠B | A=B=1 | 左项 | 右项 | 左项 | 右项 | |
| 0 | 0 | 1 | & | L+R | R | L-R | R |
| 0 | 1 | 0 | ^ | L+R | L-R | (L+R)/2 | (L-R)/2 |
| 0 | 1 | 1 | | | L | L+R | L | R-L |
| 1 | 0 | 0 | ~| | L+R | L | L-R | R |
| 1 | 0 | 1 | ~^ | L+R | R-L | (L-R)/2 | (L+R)/2 |
| 1 | 1 | 0 | ~& | R | L+R | L | R-L |
证明
& and

^ xor

| or
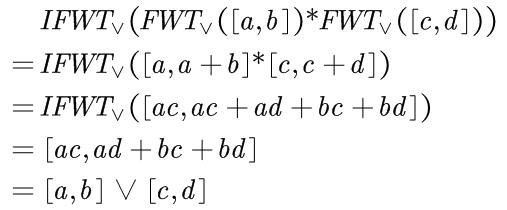
~| nor
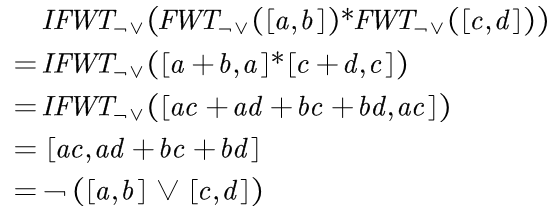
~^ nxor
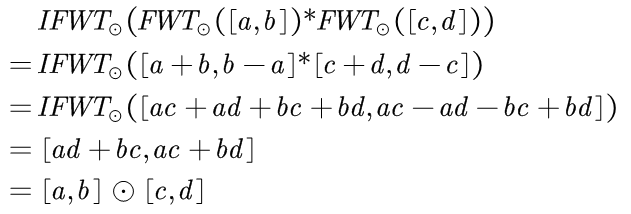
~& nand

附注
- 这里的~&,~^,~|不是直接的公式,而是按照&,^,|推导而成的,所以对同一个序列FWT+IFWT后数位会翻转
- &,^,|的FWT支持+和*,但~&,~^,~|只支持*(原因同上)
——会某人
FWT公式一览的更多相关文章
- 逻辑、集合运算上的卷积一览(FMT、FWT,……)
\oplus=\and,\or,\veebar 简介 对于逻辑\(\oplus\)的卷积,而且你不能N方豹草 \[ A_k=\sum_{i\oplus j=k} B_i\times C_k\\ \] ...
- 优秀大数据GitHub项目一览
http://blog.csdn.net/yaoxtao/article/details/50540485 优秀大数据GitHub项目一览 VMware CEO Pat Gelsinger曾说: 数据 ...
- 关于快速沃尔什变换(FWT)的一点学习和思考
最近在学FWT,抽点时间出来把这个算法总结一下. 快速沃尔什变换(Fast Walsh-Hadamard Transform),简称FWT.是快速完成集合卷积运算的一种算法. 主要功能是求:,其中为集 ...
- FWT(快速沃尔什变换)小结
在多项式卷积的处理中,我们实际上实现的是下面的一个式子 \[ C_k=\sum_{i+j=k}A_iB_j \] 然而事实上有些和(sang)蔼(xin)可(bing)亲(kuang)的出题人,并不会 ...
- [学习笔记&教程] 信号, 集合, 多项式, 以及各种卷积性变换 (FFT,NTT,FWT,FMT)
目录 信号, 集合, 多项式, 以及卷积性变换 卷积 卷积性变换 傅里叶变换与信号 引入: 信号分析 变换的基础: 复数 傅里叶变换 离散傅里叶变换 FFT 与多项式 \(n\) 次单位复根 消去引理 ...
- [HAOI2015]按位或(min-max容斥,FWT,FMT)
题目链接:洛谷 题目大意:给定正整数 $n$.一开始有一个数字 $0$,然后每一秒,都有 $p_i$ 的概率获得 $i$ 这个数 $(0\le i< 2^n)$.一秒恰好会获得一个数.每获得一个 ...
- FWT快速沃尔什变换
前言 学多项式怎么能错过\(FWT\)呢,然而这真是个毒瘤的东西,蒟蒻就只会背公式了\(\%>\_<\%\) 或卷积 \[\begin{aligned}\\ tf(A) = (tf(A_0 ...
- FWT [BZOJ 4589:Hard Nim]
4589: Hard Nim Time Limit: 10 Sec Memory Limit: 128 MBSubmit: 275 Solved: 152[Submit][Status][Disc ...
- FWT 等总结 题解
目录 与卷积: 代码: 或卷积: 代码: 异或卷积: 代码: FST:子集卷积 代码: 例题: CF914G 代码: uoj310[UNR #2]黎明前的巧克力 代码: CF662C Binary T ...
随机推荐
- jvm 这我就能会了 擦
最近老有人问jvm,恕我直言,完蛋了,不会,慢慢学吧,开始第一个学习,后续补充,走起... 我看的他的https://www.cnblogs.com/dingyingsi/p/3760447.html ...
- 如何在linux命令行无界面下使用selenium
1.安装Xvfb和pyvirtualdisplay sudo apt-get install xvfbpip install pyvirtualdisplay 2.安装chrome, chromedr ...
- NGUI的Lebal需注意问题
1,为什么调节字体大小时,字体大小没变化,我们需要调节两个地方,如下图框柱显示 调节font size和size才可以同时控制字体的大小 2,label有时是不支持输入中文,但是支持复制进去,则这时我 ...
- azkaban简单使用
步骤 1.通过web服务器创建项目,项目名称和描述都是必须填的2.上传zip包 job定义 1.简单的job一个job就是一个properties文件,只不过文件是以.job结尾,文件里面定义了job ...
- 初学Java 从控制台读取输入
代码 import java.util.Scanner; public class ComputeArea { public static void main(String[] args) { Sca ...
- GC(垃圾回收器)中的算法
GC的两种判定方法 (1) 引用计数法 给对象添加一个引用计数器,每当引用一次+1,每次失效时-1,当计数器为0时,表示对象就是不可能再被使用的. (2) 可达性分析算法 将“GC Roots”对象作 ...
- redis开发规范阿里云
一.键值设计 1.key名设计 1) 可读性和可管理性: 以业务名或数据库名为前缀,以防key冲突,用冒号分隔,比如业务名:表名:ID 2)简洁性: 保证语义的前提下,控制key的长度,当key较多 ...
- elasticsearch查询与sql对应关系
must: AND must_not:NOT should:OR
- H2database创建表
语法和sql server大同小异 create table users(id int primary key not null int identity, name varchar(20))
- join()、split()
join()用于把数组转化为字符串 var arr=['hello','world','kugou']; document.write(arr.join(''));//helloworldkugou ...
