清北学堂dp图论营游记day1

讲课人：

老师对dp的理解是类似于分治思想，由小状态推出大状态。不同的是分治算法没有重叠子问题。

dp把子问题越划越小，从而推出了基础状态。然后是dp方程，要满足简洁性，并且充分描述能够影响最后结果的条件。

转移？zhx：从小问题推到大问题就是转移。

原题链接：。

思路：先把挂钩数量排个序

这个题和导弹拦截差不多，你对l进行从大到小排序，那么文题就变成了求最长不上升子序列的个数，也就是最长上升子序列的长度。

n^2做法。

先想n^4做法，然后一步一步优化。

来道水题。

上午完结。

下午：

序列dp，区间dp

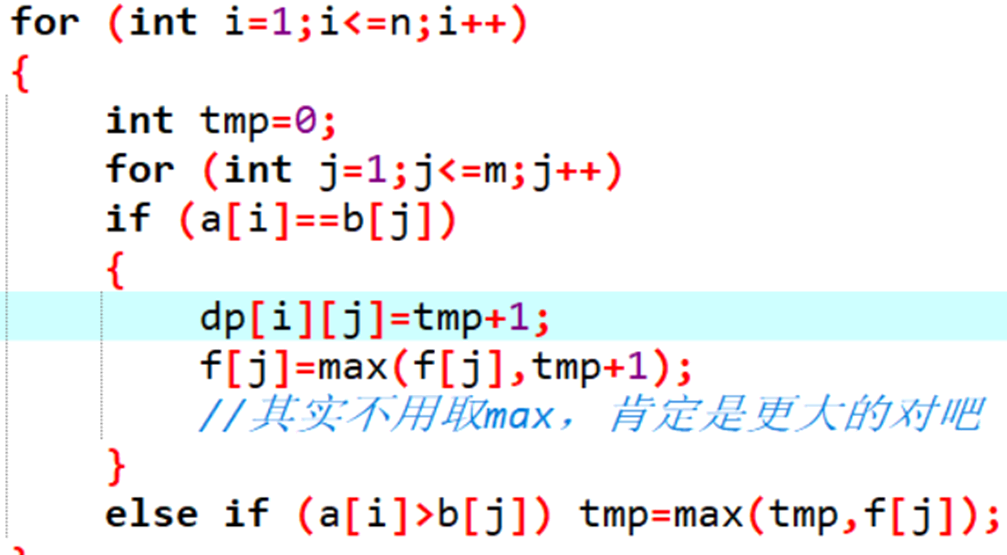
对于某个括号序列，把左右括号看成一组，对每个序列内部的括号进行消去操作，最后总能得到这样的东西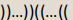：，于是我们可以吧这个题转化为另外一个题：

对于这个题，我们要为了不让血量低于0，按打怪物减少血量升序排列。

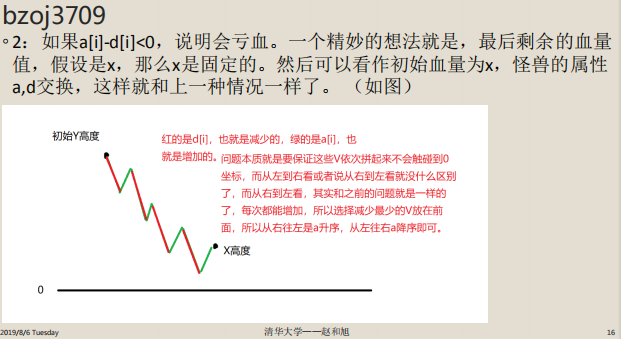
回到这个题：

这类问题：卡特兰数：

安利经典题：

代码如下：

区间dp：

转移方程：dp[i][j]=min(dp[i][k]+dp[k][j]+gcd(a[i],a[j]));很ez。

完结。zhx很强大