系统分析与设计HW8

描述软件架构与框架之间的区别与联系

• 软件架构是有关软件整体结构与组件的抽象描述，用于指导大型软件系统各个方面的设计。架构模式（style）是特定领域常见问题的解决方案。
• 框架是特定语言和技术的架构应用解决方案。
• 区别：
  • 软件架构用相对抽象的概念来描述部件的功能、部件与部件之间的协作，从而大致地描述出系统完整的运作流程。它不是实际系统的一部分。
  • 而框架是具象的概念，是实际系统的一部分。框架使用特定的语言和技术描述了架构中各部件功能的具体实现。通过使用框架，让开发者聚焦于业务逻辑代码而不是技术实现。
  • 联系：
    • 软件架构指导了框架的设计，框架通过特定的语言和技术实现了软件架构。
    • 框架可能集合了一种或多种软件架构。

以你的项目为案例

• 绘制三层架构模型图，细致到分区
• 结合你程序的结构，从程序员角度说明三层架构给开发者带来的便利
  • 分离了关注点，各部分的开发者只需要关注自己负责模块的实现。
  • 层与层之间分离后，只要接口不发生变化，层内无论如何变化甚至是重构，其他层都不受影响，大大降低了耦合程度。

研究 VUE 与 Flux 状态管理的异同

• VUE
  • vue使用vuex作为状态管理工具。vuex是Flux思想的实现之一，并在Flux的基础上做了改进。
  • vuex 包含有五个基本的对象：
    • state：存储状态。也就是变量；
    • getters：派生状态。也就是set、get中的get，有两个可选参数：state、getters分别可以获取state中的变量和其他的getters。外部调用方式：store.getters.personInfo()。
    • mutations：提交状态修改。也就是set、get中的set，这是vuex中唯一修改state的方式，但不支持异步操作。第一个参数默认是state。外部调用方式：store.commit('SET_AGE', 18)。
    • actions：和mutations类似。不过actions支持异步操作。第一个参数默认是和store具有相同参数属性的对象。外部调用方式：store.dispatch('nameAsyn')。
    • modules：store的子模块，内容就相当于是store的一个实例。调用方式和前面介绍的相似，只是要加上当前子模块名，如：store.a.getters.xxx()。
  • 个人理解：vuex通过state储存状态，获取状态应该使用getters。mutations是唯一直接修改状态的操作。actions是一系列逻辑操作，当actions需要修改状态时，它需要通过commit mutations来达到目的。而当系统比较复杂时，state对象就会变得庞大而复杂，这时候使用modules来对state进行模块划分。

  • Vuex的数据流：

    View调用store.commit提交对应的请求到Store中对应的mutation函数->store改变生成新的state(vue检测到数据变化自动渲染)

    

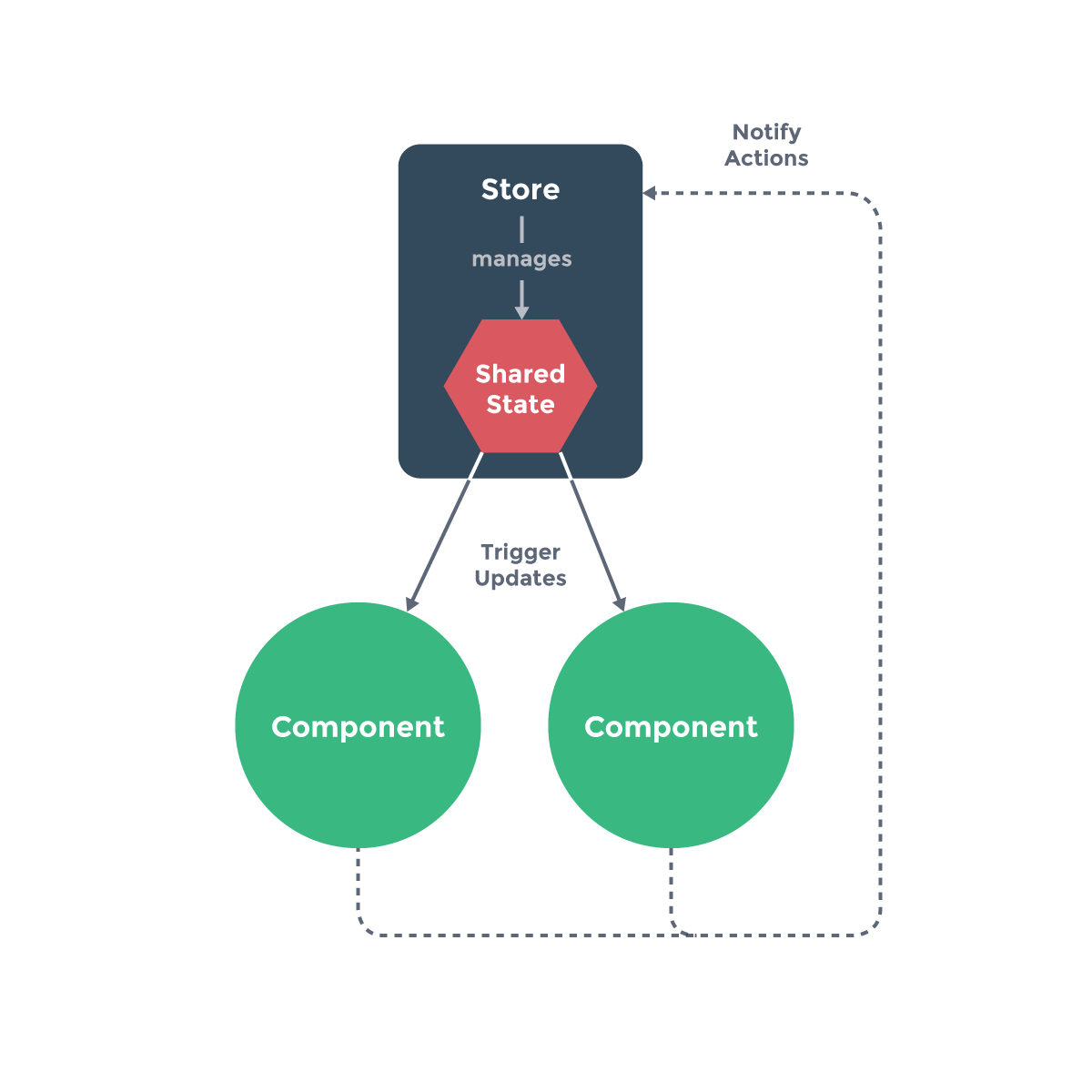
• Flux
  • Flux是facebook创建，专门用来构建前端框架结构的框架。
  • Flux包含四个基本对象：
    • action: 与vuex类似。
    • dispatcher：dispatcher将action的操作分发到不同的store。
    • store：管理状态。当store状态更新时，发布一个change事件，通知view更新视图。
    • view：监听store发布的change事件，获取新数据并提供给它的子视图。
  • 实际上vuex是基于Flux的实现，框架基本相同，但vuex将dispatcher和store合并为单独的store，并用state记录不同时间点下store的状态，方便了对状态的管理。且由于Vue自动重新渲染的特性，无需订阅重新渲染函数，只要生成新的State即可。

  • Flux的数据流：

    View发起Action->Action传递到Dispatcher->Dispatcher将通知Store->Store的状态改变通知View进行改变

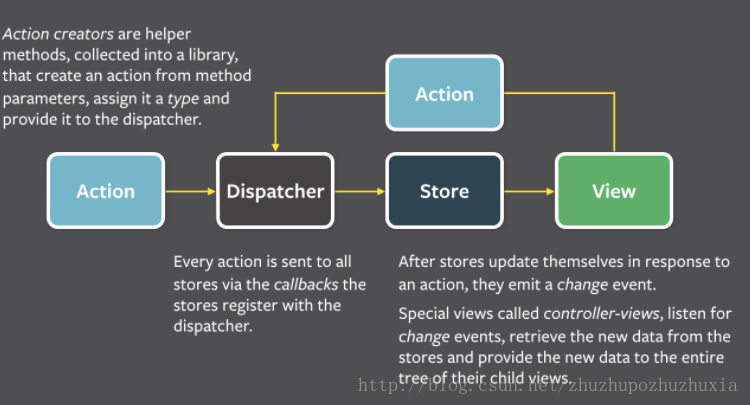
参考资料：
1.理解vuex -- vue的状态管理模式
2.Vue.js - 状态管理
3.关于Flux,Vuex,Redux的思考
4.react状态管理之flux