Size Balanced Tree(节点大小平衡树)

定义

SBT也是一种自平衡二叉查找树,它的平衡原理是每棵树的大小不小于其兄弟树的子树的大小

即size(x->l)$\ge$size(x->r->l),size(x->r->r),右边同理size(x->r)$\ge$size(x->l->l),size(x->l->r)

具体操作

　　旋转

　　　　旋转几乎是所有平衡树所共有的操作，操作方法也基本相同

　　　　

　　　　

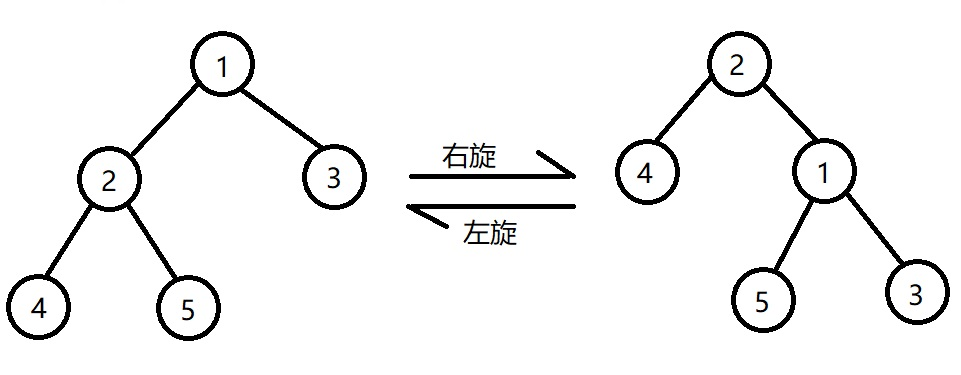
void rotate(SBT *&x,int d){//旋转操作，d=0表示左旋，d=1表示右旋
    SBT *y=x->son[d^];//y指向要旋转到父节点的子节点
    x->son[d^]=y->son[d],y->son[d]=x;//更新指向关系
    y->size=x->size;//更新size值
    x->size=size(x->son[])+size(x->son[])+x->num;
    x=y;//别忘了将进入子树的指针指到y上
}

　　平衡维护

　　　　SBT的平衡维护是SBT所特有的操作，具体有两种情况(左右对称算一种)

　　　　　　1.size(x->l)<size(x->r->r),即下图中的size(2)<size(7)

　　　　　　

　　　　　　这时我们只需要把3旋转到根即可

　　　　　　

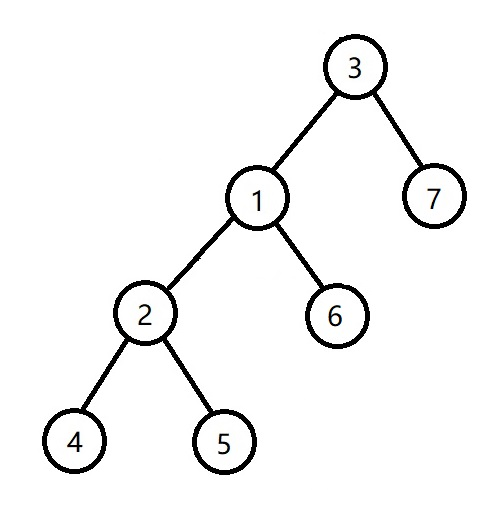
　　　　　　这时size(7)>size(2),size(6),但size(6)不一定>size(4),size(5),所以要维护一下节点1，然后再维护一遍节点3

　　　　　　2.size(x->l)<size(x->r->l),即下图中的size(2)<size(6)

　　　　　　

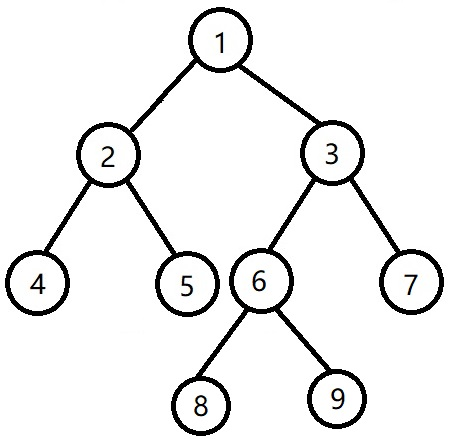
　　　　　　我们先把子树3右旋,6旋到3的位置

　　　　　　

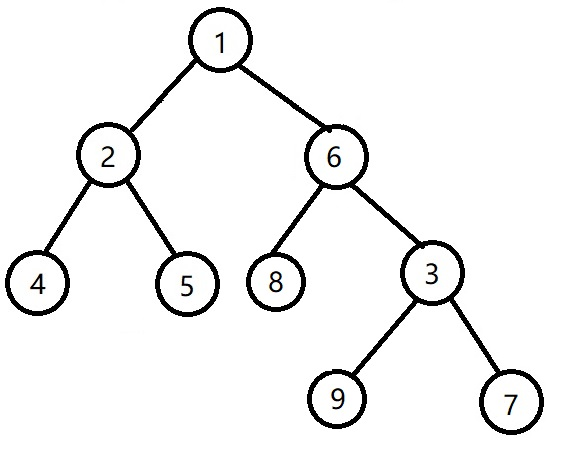
　　　　　　这时size(2)还不一定大于size(3),size(8)，于是我们把子树1左旋，将6变为根

　　　　　　

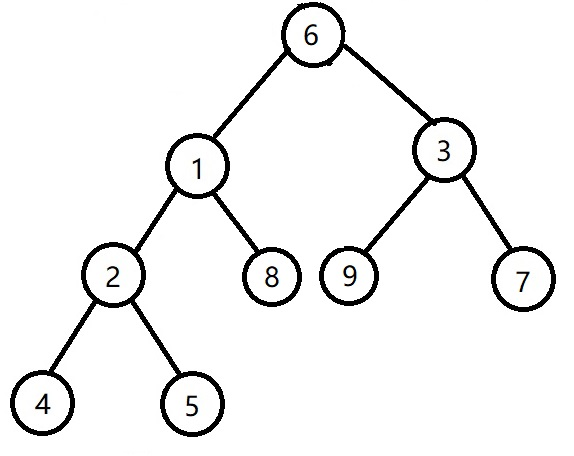
　　　　　　这时size(1)>size(9),size(7)，但是子树1和3不一定平衡，所以平衡1，3，然后再平衡6

void maintain(SBT *&x,int d){//平衡操作,检查(x->son[d]的子树是否比x->son[d^1]大)
    if(x->son[d]==NULL)return;
    if(size(x->son[d^])<size(x->son[d]->son[d^]))rotate(x->son[d],d),rotate(x,d^);
    else if(size(x->son[d^])<size(x->son[d]->son[d]))rotate(x,d^);
    else return;
    maintain(x->son[],),maintain(x->son[],),maintain(x,),maintain(x,);//平衡子树后再平衡一次x
}

　　　插入

　　　　　　和二叉查找树的插入差不多，只是在插入后要平衡一下

void insert(SBT *&x,int key){
    if(!x){x=new SBT(key);return;}
    x->size++;
    if(x->key==key){x->num++;return;}
    int d=key>x->key;
    insert(x->son[d],key);
    maintain(x,d);//插入后平衡一遍
}

　　　删除

　　　　　　如果要删除的节点有子节点为空，则用另一个子节点代替要删除的节点
　　　　　　否则，用后继代替当前节点，然后递归删除后继

void del(SBT *&x,int key){
    if(x->key!=key){
        del(x->son[key>x->key],key);
        x->size=size(x->son[])+size(x->son[])+x->num;
        return;
    }
    x->size--;
    if(x->num>){x->num--;return;}//num
    SBT *p=x;
    if(x->son[]==NULL)x=x->son[],delete p;
    else if(x->son[]==NULL)x=x->son[],delete p;
    else{//用后继替换当前节点，删除后继
        p=x->son[];
        while(p->son[]){
            p=p->son[];
        }
        x->num=p->num,x->key=p->key,p->num=,del(x->son[],p->key);
    }
}

其他操作

int query_id(SBT *x,int key){//求数列中比key小的有几个
    if(!x)return ;
    if(x->key>key)return query_id(x->son[],key);
    if(x->key==key)return size(x->son[]);
    return query_id(x->son[],key)+size(x->son[])+x->num;
}
int query_k(SBT *x,int k){//求排第k的数
    if(!x)return ;
    if(size(x->son[])>=k)return query_k(x->son[],k);
    if(size(x->son[])+x->num>=k)return x->key;
    return query_k(x->son[],k-size(x->son[])-x->num);
}
int ans;
void pre(SBT *x,int num){//求num的前驱(即小于num的最大的数)，并存在ans里
    if(!x)return;
    if(x->key<num)ans=x->key,pre(x->son[],num);
    else pre(x->son[],num);
}
void suc(SBT *x,int num){//求后继
    if(!x)return;
    if(x->key>num)ans=x->key,suc(x->son[],num);
    else suc(x->son[],num);
}
void mid_traversal(SBT *x){//中序遍历
    if(x->son[])mid_traversal(x->son[]);
    printf("%d ",x->key);
    if(x->son[])mid_traversal(x->son[]);
}

模板

#include<cstdio>
#include<cstring>
using namespace std;
#define size(x) (x?x->size:0)
struct SBT{
    int key,size,num;
    SBT *son[];
    SBT(){
        memset(this,,sizeof(SBT));
    }
    SBT(int x){
        num=size=,key=x,son[]=son[]=;
    }
}*root;
void rotate(SBT *&x,int d){//旋转操作，d=0表示左旋，d=1表示右旋
    SBT *y=x->son[d^];//y指向要旋转到父节点的子节点
    x->son[d^]=y->son[d],y->son[d]=x;//更新指向关系
    y->size=x->size;//更新size值
    x->size=size(x->son[])+size(x->son[])+x->num;
    x=y;//别忘了将进入子树的指针指到y上
}
void maintain(SBT *&x,int d){//平衡操作,检查(x->son[d]的子树是否比x->son[d^1]大)
    if(x->son[d]==NULL)return;
    if(size(x->son[d^])<size(x->son[d]->son[d^]))rotate(x->son[d],d),rotate(x,d^);
    else if(size(x->son[d^])<size(x->son[d]->son[d]))rotate(x,d^);
    else return;
    maintain(x->son[],),maintain(x->son[],),maintain(x,),maintain(x,);//平衡子树后再平衡一次x
}
void insert(SBT *&x,int key){
    if(!x){x=new SBT(key);return;}
    x->size++;
    if(x->key==key){x->num++;return;}
    int d=key>x->key;
    insert(x->son[d],key);
    maintain(x,d);//插入后平衡一遍
}
void del(SBT *&x,int key){
    if(x->key!=key){
        del(x->son[key>x->key],key);
        x->size=size(x->son[])+size(x->son[])+x->num;
        return;
    }
    x->size--;
    if(x->num>){x->num--;return;}//num>1直接num-1即可
    SBT *p=x;
    if(x->son[]==NULL)x=x->son[],delete p;
    else if(x->son[]==NULL)x=x->son[],delete p;
    else{//用后继替换当前节点，删除后继
        p=x->son[];
        while(p->son[]){
            p=p->son[];
        }
        x->num=p->num,x->key=p->key,p->num=,del(x->son[],p->key);
    }
}
int query_id(SBT *x,int key){//求数列中比key小的有几个
    if(!x)return ;
    if(x->key>key)return query_id(x->son[],key);
    if(x->key==key)return size(x->son[]);
    return query_id(x->son[],key)+size(x->son[])+x->num;
}
int query_k(SBT *x,int k){//求排第k的数
    if(!x)return ;
    if(size(x->son[])>=k)return query_k(x->son[],k);
    if(size(x->son[])+x->num>=k)return x->key;
    return query_k(x->son[],k-size(x->son[])-x->num);
}
int ans;
void pre(SBT *x,int num){//求num的前驱(即小于num的最大的数)，并存在ans里
    if(!x)return;
    if(x->key<num)ans=x->key,pre(x->son[],num);
    else pre(x->son[],num);
}
void suc(SBT *x,int num){//求后继
    if(!x)return;
    if(x->key>num)ans=x->key,suc(x->son[],num);
    else suc(x->son[],num);
}
void mid_traversal(SBT *x){//中序遍历
    if(x->son[])mid_traversal(x->son[]);
    printf("%d ",x->key);
    if(x->son[])mid_traversal(x->son[]);
}
bool f=;
void check(SBT *x){
    if(!x)return;
    check(x->son[]);
    check(x->son[]);
    if(x->size!=size(x->son[])+size(x->son[])+)printf("woring");
}
int main(){
    return ;
}

例题P3369 【模板】普通平衡树（Treap/SBT）

#include<cstdio>
#include<cstring>
using namespace std;
#define size(x) (x?x->size:0)
struct SBT{
    int key,size,num;
    SBT *son[];
    SBT(){
        memset(this,,sizeof(SBT));
    }
    SBT(int x){
        num=size=,key=x,son[]=son[]=;
    }
}*root;
void rotate(SBT *&x,int d){//旋转操作，d=0表示左旋，d=1表示右旋
    SBT *y=x->son[d^];//y指向要旋转到父节点的子节点
    x->son[d^]=y->son[d],y->son[d]=x;//更新指向关系
    y->size=x->size;//更新size值
    x->size=size(x->son[])+size(x->son[])+x->num;
    x=y;//别忘了将进入子树的指针指到y上
}
void maintain(SBT *&x,int d){//平衡操作,检查(x->son[d]的子树是否比x->son[d^1]大)
    if(x->son[d]==NULL)return;
    if(size(x->son[d^])<size(x->son[d]->son[d^]))rotate(x->son[d],d),rotate(x,d^);
    else if(size(x->son[d^])<size(x->son[d]->son[d]))rotate(x,d^);
    else return;
    maintain(x->son[],),maintain(x->son[],),maintain(x,),maintain(x,);//平衡子树后再平衡一次x
}
void insert(SBT *&x,int key){
    if(!x){x=new SBT(key);return;}
    x->size++;
    if(x->key==key){x->num++;return;}
    int d=key>x->key;
    insert(x->son[d],key);
    maintain(x,d);//插入后平衡一遍
}
void del(SBT *&x,int key){
    if(x->key!=key){
        del(x->son[key>x->key],key);
        x->size=size(x->son[])+size(x->son[])+x->num;
        return;
    }
    x->size--;
    if(x->num>){x->num--;return;}//num>1直接num-1即可
    SBT *p=x;
    if(x->son[]==NULL)x=x->son[],delete p;
    else if(x->son[]==NULL)x=x->son[],delete p;
    else{//用后继替换当前节点，删除后继
        p=x->son[];
        while(p->son[]){
            p=p->son[];
        }
        x->num=p->num,x->key=p->key,p->num=,del(x->son[],p->key);
    }
}
int query_id(SBT *x,int key){//求数列中比key小的有几个
    if(!x)return ;
    if(x->key>key)return query_id(x->son[],key);
    if(x->key==key)return size(x->son[]);
    return query_id(x->son[],key)+size(x->son[])+x->num;
}
int query_k(SBT *x,int k){//求排第k的数
    if(!x)return ;
    if(size(x->son[])>=k)return query_k(x->son[],k);
    if(size(x->son[])+x->num>=k)return x->key;
    return query_k(x->son[],k-size(x->son[])-x->num);
}
int ans;
void pre(SBT *x,int num){//求num的前驱(即小于num的最大的数)，并存在ans里
    if(!x)return;
    if(x->key<num)ans=x->key,pre(x->son[],num);
    else pre(x->son[],num);
}
void suc(SBT *x,int num){//求后继
    if(!x)return;
    if(x->key>num)ans=x->key,suc(x->son[],num);
    else suc(x->son[],num);
}
void mid_traversal(SBT *x){//中序遍历
    if(x->son[])mid_traversal(x->son[]);
    printf("%d ",x->key);
    if(x->son[])mid_traversal(x->son[]);
}
bool f=;
void check(SBT *x){
    if(!x)return;
    check(x->son[]);
    check(x->son[]);
    if(x->size!=size(x->son[])+size(x->son[])+)printf("woring");
}
int main(){
    freopen("1.in","r",stdin);
    freopen("1.out","w",stdout);
    int n,x,y;scanf("%d",&n);
    while(n--){
        scanf("%d%d",&x,&y);
        switch(x){
            case :
                insert(root,y);
                break;
            case :
                del(root,y);
                break;
            case :
                printf("%d\n",query_id(root,y)+);
                break;
            case :
                printf("%d\n",query_k(root,y));
                break;
            case :
                pre(root,y);printf("%d\n",ans);
                break;
            default:
                suc(root,y);printf("%d\n",ans);

        }
//        mid_traversal(root);printf("\n");
    }
    return ;
}