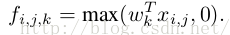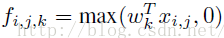深度学习（二十六）Network In Network学习笔记

深度学习（二十六）Network In Network学习笔记

Network In Network学习笔记

原文地址：http://blog.csdn.net/hjimce/article/details/50458190

作者：hjimce

一、相关理论

本篇博文主要讲解2014年ICLR的一篇非常牛逼的paper：《Network In Network》，过去一年已经有了好几百的引用量，这篇paper改进了传统的CNN网络，采用了少量的参数就松松击败了Alexnet网络，Alexnet网络参数大小是230M，采用这篇paper的算法才29M，减小了将近10倍啊。这篇paper提出的网络结构，是对传统CNN网络的一种改进(这种文献少之又少，所以感觉很有必要学习)。

传统的卷积神经网络一般来说是由：线性卷积层、池化层、全连接层堆叠起来的网络。卷积层通过线性滤波器进行线性卷积运算，然后在接个非线性激活函数，最终生成特征图。以Relu激活函数为例，特征图的计算公式为：

其中（i，j）表示图片像素点的位置索引，xij表示我们卷积窗口中的图片块，k则表示我们要提取的特征图的索引。

一般来说，如果我们要提取的一些潜在的特征是线性可分的话，那么对于线性的卷积运算来说这是足够了。然而一般来说我们所要提取的特征一般是高度非线性的。在传统的CNN中，也许我们可以用超完备的滤波器，来提取各种潜在的特征。比如我们要提取某个特征，于是我就用了一大堆的滤波器，把所有可能的提取出来，这样就可以把我想要提取的特征也覆盖到，然而这样存在一个缺点，那就是网络太恐怖了，参数太多了。

我们知道CNN高层特征其实是低层特征通过某种运算的组合。于是作者就根据这个想法，提出在每个局部感受野中进行更加复杂的运算，提出了对卷积层的改进算法：MLP卷积层。另一方面，传统的CNN最后一层都是全连接层，参数个数非常之多，容易引起过拟合（如Alexnet）,一个CNN模型，大部分的参数都被全连接层给占用了，故这篇paper提出采用了：全局均值池化，替代全连接层。因此后面主要从这两个创新点进行讲解。

二、MLP卷积层(文献创新点1)

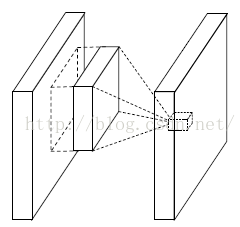
这个是文献的大创新点，也就是提出了mlpconv层。Mlpconv层可以看成是每个卷积的局部感受野中还包含了一个微型的多层网络。其实在以前的卷积层中，我们局部感受野窗口的运算，可以理解为一个单层的网络，如下图所示：

线性卷积层

CNN层的计算公式如下：

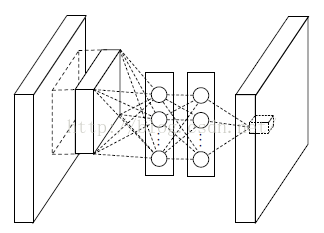
然而现在不同了，我们要采用多层的网络，提高非线性，于是mlpconv层的网络结构图如下：：

Mlpconv层

从上面的图可以看到，说的简单一点呢，利用多层mlp的微型网络，对每个局部感受野的神经元进行更加复杂的运算，而以前的卷积层，局部感受野的运算仅仅只是一个单层的神经网络罢了。对于mlpconv层每张特征图的计算公式如下：

一般来说mlp是一个三层的网络结构。

下面是一个单层的mlpconv网络的caffe网络结构文件，源码来自于：https://gist.github.com/mavenlin/d802a5849de39225bcc6 ：

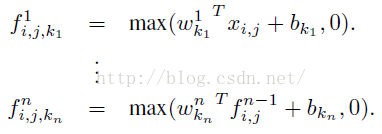
1. 三、全局均值池化(文献创新点2)

传统的卷积神经网络卷积运算一般是出现在低层网络。对于分类问题，最后一个卷积层的特征图通过量化然后与全连接层连接，最后在接一个softmax逻辑回归分类层。这种网络结构，使得卷积层和传统的神经网络层连接在一起。我们可以把卷积层看做是特征提取器，然后得到的特征再用传统的神经网络进行分类。

然而，全连接层因为参数个数太多，往往容易出现过拟合的现象，导致网络的泛化能力不尽人意。于是Hinton采用了Dropout的方法，来提高网络的泛化能力。

本文提出采用全局均值池化的方法，替代传统CNN中的全连接层。与传统的全连接层不同，我们对每个特征图一整张图片进行全局均值池化，这样每张特征图都可以得到一个输出。这样采用均值池化，连参数都省了，可以大大减小网络，避免过拟合，另一方面它有一个特点，每张特征图相当于一个输出特征，然后这个特征就表示了我们输出类的特征。这样如果我们在做1000个分类任务的时候，我们网络在设计的时候，最后一层的特征图个数就要选择1000，下面是《Network In Network》网络的源码，倒数一层的网络相关参数：

全局均值池化层的相关参数如下：

因为在Alexnet网络中，最后一个卷积层输出的特征图大小刚好是6*6,所以我们pooling的大小选择6，方法选择：AVE。

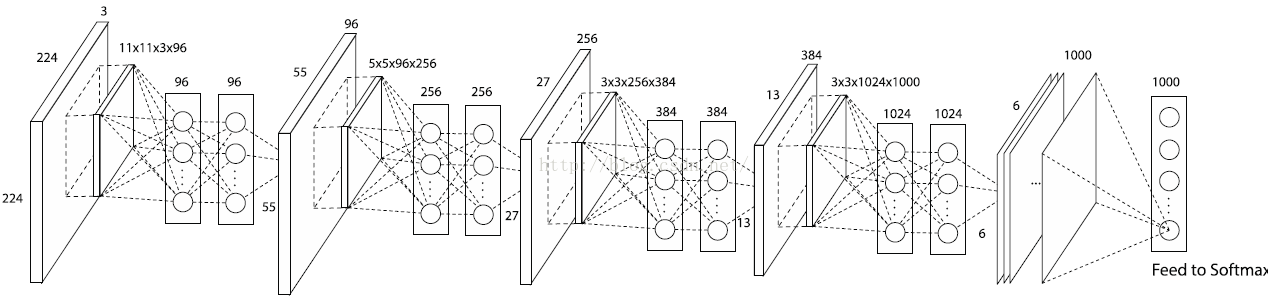
四、总体网络架构

根据上面的作者对传统CNN的两个改进，利用其进行1000物体分类问题，于是作者最后设计了一个：4层的NIN+全局均值池化，网络如下：

个人总结：个人感觉这篇文献很有价值，实现方式也很简单，一开始我还以为需要caffe的c++源码来实现NIN网络，结果发现实现NIN的源码实现方式其实就是一个1*1的卷积核，实现卷积运算，所以实现起来相当容易，不需要自己写源码，只需要简简单单的把卷积核的大小变一下，然后最后一层的全连接层直接用avg pooling替换一下就ok了。个人评价：网络浅显易懂，简单实现，却可以改进原来的网络，提高精度，减小模型大小，所以是一篇很值得学习的文献。后续即将讲解另外几篇2015年，也是对CNN网络结构改进的牛逼文献：《Spatial Transformer Networks》、《Striving For Simplicity：The All Convolutional Net》、《Stacked What-Where Auto-encoders》，敬请期待，毕竟这样的文章敢于挑战传统的CNN结构，对其不知做出改进，所以我们需要一篇一篇的学。

参考文献：

1、《Network In Network》

2、https://github.com/BVLC/caffe/wiki/Model-Zoo

3、https://gist.github.com/mavenlin/d802a5849de39225bcc6

4、《Maxout Networks》

**********************作者：hjimce   时间：2016.1.4  联系QQ：1393852684     原创文章，版权所有，转载请保留本行信息***************