量子搜索算法 Grover search

问题定义：

Problem：

$f: \{ 0,1,2,3,……,N-1 \} \rightarrow \{0,1\}$

找到 $f(x)=1$ 的x

解法

经典解法：

经典解法很简单，就是把每一个都看一遍，如果只有一个x对应的f(x)=1，那么平均是要看一半，才能找到那个x。

时间复杂度O(N)

量子解法：

使用Grover search 算法，时间复杂度在 $O(\sqrt N)$

Grover search 算法

Grover search 算法一共分为两步：

Phase Inversion
Inversion about the Mean

然后不断的迭代这两步我们就能够得到结果了。

首先我们先看看这两个步骤分别在做什么：

我们把 $f(x)=1 $ 的 $|x\rangle$ 称为 $x^*$ ，我们要找的也就是这个 $x^*$ 。

Phase Inversion:

这一步主要是把 $x^*$ 的概率幅翻转，变成负数，而其他的保持不变。

即，把 $\sum_{x } \alpha_x|x\rangle$ 变成 $\sum_{x \neq x^*} \alpha_x|x\rangle -\alpha_{x^*}|x^*\rangle$

Inversion about the Mean

这一步呢，就是把 $\alpha_x$ 变成 $2\mu- \alpha_x$

$\mu$ 是所有概率幅的平均值，$\mu= \frac{\sum_x \alpha_x}{N}$

用图可能更好表达这两个步骤究竟在做什么：

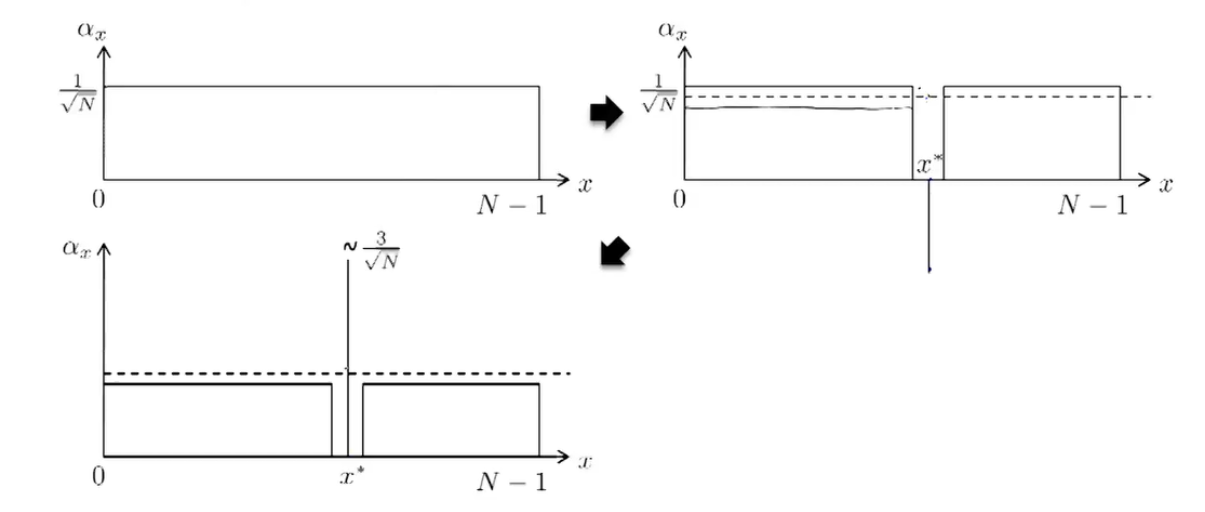
图1到图2，就是Phase Inversion，把$x^*$的概率幅翻转到了下面，图2中的虚线就是我的概率幅的平均值，图2到图3 就是我们的Inversion about the Mean，对着平均值翻转一次，其余x的概率幅是高于平均值的，所以 $2\mu- \alpha_x$ 让他们变小了，而我们的 $x^*$ 他的概率幅是个负数，所以 $2\mu- \alpha_x$ 后他增加了。

不断的重复这个步骤， $x^*$ 他的概率幅会越来越大，最后我们测量的时候就会很容的找到他。

进行了 $\sqrt N$ 后，他的概率幅就会达到 $\frac{1}{ \sqrt 2}$ ，算概率就是1/2。

那么接下来的问题就是，这些操作是怎么实现的？

Phase Inversion:

这个步骤要做的事情就是，

把 $\sum_{x } \alpha_x|x\rangle$ 变成 $\sum_{x \neq x^*} \alpha_x|x\rangle -\alpha_{x^*}|x^*\rangle$

符号是和f(x)是否为1相关的，进一步化简就是 $\sum_x (-1)^{f(x)} \alpha_x|x\rangle$

有没有一丝熟悉感？

把f(x)的结果给放到相位上去，这是我们在Parity Problem中就遇到的问题。

当时的解决方法是把答案比特变成 $|-\rangle$。

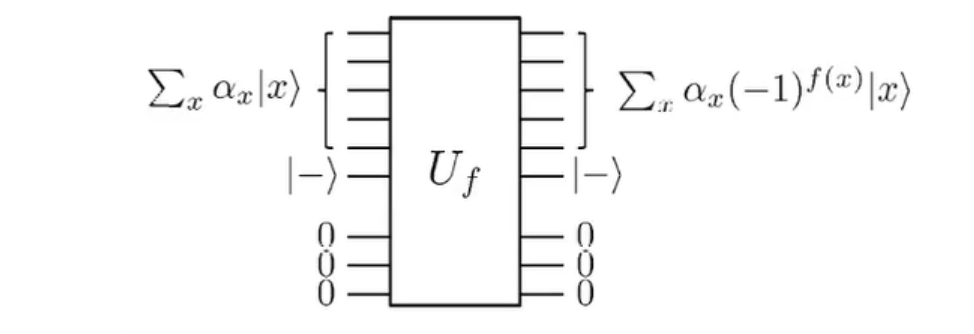
一般情况，如果我们打算放置答案的比特是 $|b\rangle$，那么输入的比特就是$|b \oplus f(x)\rangle$

如果f(x)=0 那么$|( \frac{1}{\sqrt2}|0\rangle-\frac{1}{\sqrt2}|1\rangle) \oplus f(x) \rangle = \frac{1}{\sqrt2}|0\rangle-\frac{1}{\sqrt2}|1\rangle = |-\rangle$

如果f(x)=1 那么$( \frac{1}{\sqrt2}|0\rangle-\frac{1}{\sqrt2}|1\rangle) \oplus f(x) \rangle = \frac{1}{\sqrt2}|1\rangle-\frac{1}{\sqrt2}|0\rangle = -|-\rangle$

最后一个比特的值如果在$|+\rangle |-\rangle$坐标下测量，一定是 $|-\rangle$，f(x)的差别也变到了符号上，即 $(-1)^{f(x)}$

Inversion about the Mean

把 $\alpha_x$ 变成 $2\mu- \alpha_x$ ，这个就要比前一个麻烦了

这其实是要求我把现在的态对着 $\mu$ 翻转。

对着 $\mu$ 翻转会吗？

不太会。

但是我会对着 $|0\rangle$ 的翻转啊。

对角线第一个值为1，其余为-1，非对角线的都为0。

$\left[ \begin{array}{} 1 & 0 & …& 0 \\ 0 & -1 & …& 0 \\…\\0 & 0 & …& -1 \end{array}\right]\left[ \begin{array}{} a_0\\a_1\\…\\a_{n-1} \end{array}\right]=\left[ \begin{array}{} a_0\\-a_1\\…\\-a_{n-1} \end{array}\right]$

这个矩阵轻而易举的可以让 $|0\rangle$ 保持不变，非 $|0\rangle$ 的符号全都翻转。

量子变换要求矩阵式酉矩阵，这个矩阵很明显满足 $UU^\dagger=U^\dagger U=I$

接下来怎么做呢？

$|\mu\rangle$ 是一个怎样的态？

所有的x的概率都一样，也就是我们的superposition $\frac{1}{2^{\frac{n}{2}}} \sum_{x \in \{0,1 \}^n}|x\rangle$

$\frac{1}{2^{\frac{n}{2}}} \sum_{x \in \{0,1 \}^n}|x\rangle$ 和 $|0\rangle$之间的相互转换，这就是我们最最熟悉的Hadamard Transform了

第二部分的电路图如下：

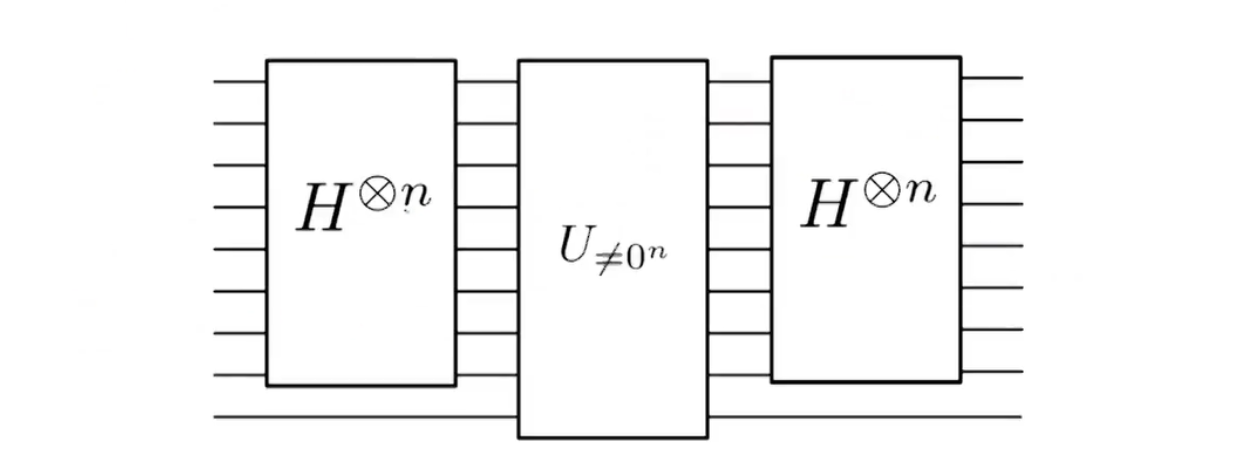
这个矩阵是可以直接计算的：

我这里直接给出答案，得到的矩阵值呢是下图左边的这个矩阵：

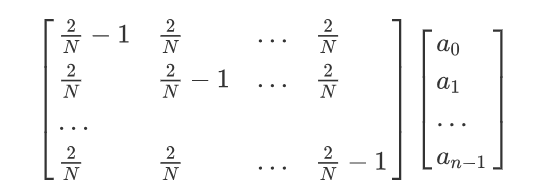
在对应的 $\alpha_x$的结果恰好是 $\frac{2}{N} \sum _{y=0}^{N} \alpha_y -\alpha_x$

而 $\frac{2}{N} \sum _{y=0}^{N} \alpha_y$ 恰好就是 $2\mu$

至此，呈上最完整的电路图模块：

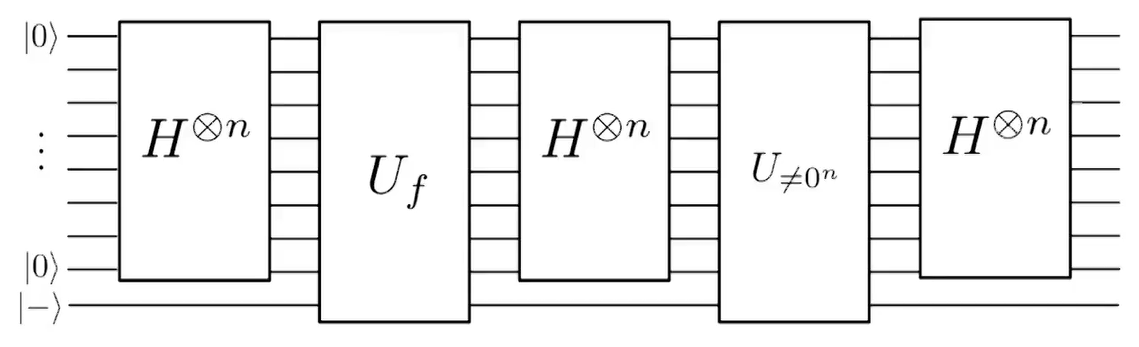
第一个H门是数据的初始化，第二个门是为了翻转 $x^*$，第三四五个门是为了对 $| \mu \rangle$ 翻转，二三四五这四个门就是要给重复的模块了，不断的重复他们就可以不断的提高 $x^*$的概率幅，最终找到 $x^*$。

参考资料：

Quantume Mechanics & Quantume Computation Lecture 11