poj1523 求割点 tarjan

SPF

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 7678		Accepted: 3489

Description

Consider the two networks shown below. Assuming that data moves around these networks only between directly connected nodes on a peer-to-peer basis, a failure of a single node, 3, in the network on the left would prevent some of the still available nodes from communicating with each other. Nodes 1 and 2 could still communicate with each other as could nodes 4 and 5, but communication between any other pairs of nodes would no longer be possible.

Node 3 is therefore a Single Point of Failure (SPF) for this network. Strictly, an SPF will be defined as any node that, if unavailable, would prevent at least one pair of available nodes from being able to communicate on what was previously a fully connected network. Note that the network on the right has no such node; there is no SPF in the network. At least two machines must fail before there are any pairs of available nodes which cannot communicate.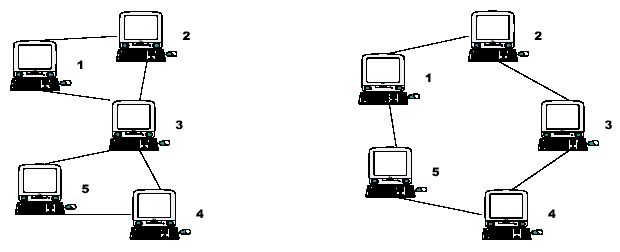 

Input

The input will contain the description of several networks. A network description will consist of pairs of integers, one pair per line, that identify connected nodes. Ordering of the pairs is irrelevant; 1 2 and 2 1 specify the same connection. All node numbers will range from 1 to 1000. A line containing a single zero ends the list of connected nodes. An empty network description flags the end of the input. Blank lines in the input file should be ignored.

Output

For each network in the input, you will output its number in the file, followed by a list of any SPF nodes that exist.

The first network in the file should be identified as "Network #1", the second as "Network #2", etc. For each SPF node, output a line, formatted as shown in the examples below, that identifies the node and the number of fully connected subnets that remain when that node fails. If the network has no SPF nodes, simply output the text "No SPF nodes" instead of a list of SPF nodes.

Sample Input

1 2
5 4
3 1
3 2
3 4
3 5
0

1 2
2 3
3 4
4 5
5 1
0

1 2
2 3
3 4
4 6
6 3
2 5
5 1
0

0

Sample Output

Network #1
  SPF node 3 leaves 2 subnets

Network #2
  No SPF nodes

Network #3
  SPF node 2 leaves 2 subnets
  SPF node 3 leaves 2 subnets

题意: 求割点 同时求出删除当前点后，分成几个连通分量。

思路:

tarjan算法求割点。 tarjan处理强连通 其实都是基于dfs的。同时维护2个数组。 dfn[] 和 low[] 分别表示第i点时的深度，和通过能够到达的祖先的深度。

求强连通的时候，如果low[i] == dfn[i] 说明栈内当前点以上的点 都是强连通块里面的。也就是说i的子树中不能到达i的祖先。

在求割点的时候，如果low[v] > dfn[u]（v是u的子节点）说明v不能到达u的祖先 说明删除u后 v的子树从原图中分离。

#include<set>
#include<map>
#include<queue>
#include<stack>
#include<cmath>
#include<string>
#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define INF 1000000001
#define MOD 1000000007
#define ll long long
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define pi acos(-1.0)
using namespace std;
const int MAXN = ;
struct node
{
    int to;
    int next;
}edge[MAXN*];
int ind,pre[MAXN],dfn[MAXN],low[MAXN],num[MAXN],n,vis[MAXN];
void add(int x,int y)
{
    edge[ind].to = y;
    edge[ind].next = pre[x];
    pre[x] = ind ++;
}
void dfs(int rt,int d)
{
    vis[rt] = ;
    dfn[rt] = low[rt] = d;
    for(int i = pre[rt]; i != -; i = edge[i].next){
        int t = edge[i].to;
        if(!vis[t]){
            dfs(t,d + );
            low[rt] = min(low[rt],low[t]);
            if(low[t] >= dfn[rt]){
                num[rt] ++;
            }
        }
        else {
            low[rt] = min(low[rt],dfn[t]);
        }
    }
}
int main()
{
    int x,y,ff = ;
    while(){
        n = ;
        scanf("%d",&x);
        if(!x)break;
        scanf("%d",&y);
        ind = , memset(pre,-,sizeof(pre));
        add(x,y), add(y,x);
        n = max(x,y);
        while(){
            scanf("%d",&x);
            if(!x)break;
            scanf("%d",&y);
            n = max(n,x);
            n = max(n,y);
            add(x,y), add(y,x);
        }
        memset(vis,,sizeof(vis));
        memset(dfn,,sizeof(dfn));
        memset(low,,sizeof(low));
        memset(num,,sizeof(num));
        dfs(,);
        int flag = ;
        if(ff >= )printf("\n");
        printf("Network #%d\n",++ff);
        num[] = num[] ? num[] -  : ;
        for(int i = ; i <= n; i++){
            if(num[i]){
                flag = ;
                printf("  SPF node %d leaves %d subnets\n",i,num[i] + );
            }
        }
        if(!flag){
            printf("  No SPF nodes\n");
        }
    }
    return ;
}