hdu.1111.Secret Code(dfs + 秦九韶算法)
Secret Code
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others) Total Submission(s): 670 Accepted Submission(s): 109
But an almost unknown archaeologist has obtained a copy of the code something during the 18th century. He was afraid that the code could get to the ``wrong people'' so he has encoded the numbers in a very special way. He took a random complex number B that was greater (in absolute value) than any of the encoded numbers. Then he counted the numbers as the digits of the system with basis B. That means the sequence of numbers an, an-1, ..., a1, a0 was encoded as the number X = a0 + a1B + a2B2 + ...+ anBn.
Your goal is to decrypt the secret code, i.e. to express a given number X in the number system to the base B. In other words, given the numbers X and Byou are to determine the ``digit'' a0 through an.
-935 2475 -11 -15
1 0 -3 -2
93 16 3 2
191 -192 11 -12
1
The code cannot be decrypted.
16,15
#include<stdio.h>
#include<string.h>
const int M = ;
typedef __int64 ll ;
ll xr , xi , br , bi ;
int n ;
ll ini ;
ll a[M] ;
ll t ; bool dfs (ll l , ll r , int dep)
{
if (dep > ) return false ;
if (l == && r == ) {
n = dep ;
return true ;
}
ll al , ar ;
for (int i = ; i * i < ini ; i ++) {
al = l - i ; ar = r ;
if ( ( (1ll * al * br + 1ll *ar * bi) % t ) == && ((1ll *ar * br -1ll * al * bi) % t) == ) {
a[dep] = i ;
if ( dfs ( ((1ll * al * br + 1ll * ar * bi) / t) , ((1ll * ar * br - 1ll * al * bi) / t) , dep + ) )
return true ;
}
}
return false ;
} int main ()
{
//freopen ("a.txt" , "r" , stdin ) ;
ll T ;
scanf ("%I64d" , &T ) ;
while (T --) {
scanf ("%I64d%I64d%I64d%I64d" , &xr , &xi , &br , &bi ) ;
t = br * br + bi * bi ;
ini = br * br + bi * bi ;
if (dfs (xr , xi , ) ) {
if (n == ) puts ("") ;
else {
for (int i = n - ; i >= ; i --) printf ("%I64d%c" , a[i] , i == ? '\n' : ',') ;
}
}
else puts ("The code cannot be decrypted.") ;
}
return ;
}
秦九韶算法:
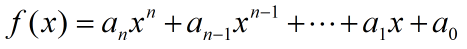
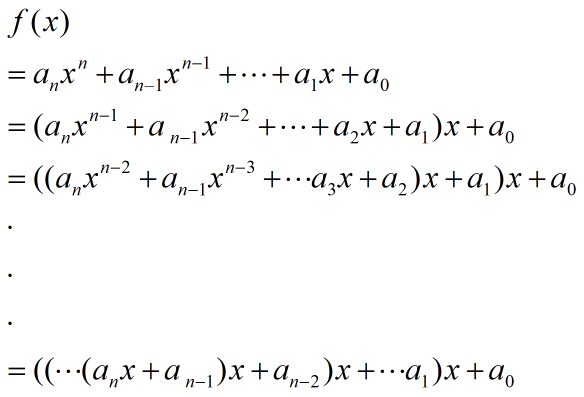
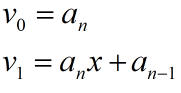

hdu.1111.Secret Code(dfs + 秦九韶算法)的更多相关文章
- HDU 1111 Secret Code (DFS)
题目链接 题意 : 给你复数X的Xr和Xi,B的Br和Bi,让你求一个数列,使得X = a0 + a1B + a2B2 + ...+ anBn,X=Xr+i*Xi,B=Br+Bi*i : 思路 : 首 ...
- HDU 1111 Secret Code(数论的dfs)
Secret Code Time Limit:1000MS Memory Limit:32768KB 64bit IO Format:%I64d & %I64u Submit ...
- hdu 1111 Secret Code
http://acm.hdu.edu.cn/showproblem.php?pid=1111 复数除法: #include <cstdio> #include <cstring> ...
- [swustoj 679] Secret Code
Secret Code 问题描述 The Sarcophagus itself is locked by a secret numerical code. When somebody wants to ...
- 秦九韶算法 & 三分法
前言 今天考试出了一个题 郭郭模拟退火骗了75分 于是再次把咕咕了好久的模退提上日程 如果进展顺利 明后天应该会开爬山算法和模退的博客笔记 今天先把今天考试的正解学习一下--三分法 引入 老规矩上板子 ...
- Android Secret Code
我们很多人应该都做过这样的操作,打开拨号键盘输入*#*#4636#*#*等字符就会弹出一个界面显示手机相关的一些信息,这个功能在Android中被称为android secret code,除了这些系 ...
- bzoj3157国王奇遇记(秦九韶算法+矩乘)&&bzoj233AC达成
bz第233题,用一种233333333的做法过掉了(为啥我YY出一个算法来就是全网最慢的啊...) 题意:求sigma{(i^m)*(m^i),1<=i<=n},n<=10^9,m ...
- Android 编程下的 Secret Code
我们很多人应该都做过这样的操作,打开拨号键盘输入 *#*#4636#*#* 等字符就会弹出一个界面显示手机相关的一些信息,这个功能在 Android 中被称为 Android Secret Code, ...
- The secret code
The secret code Input file: stdinOutput file: stTime limit: 1 sec Memory limit: 256 MbAfter returnin ...
随机推荐
- Session对象
Session对象用于存储在多个页面调用之间特定用户的信息.Session对象只针对单一网站使用者,不同的客户端无法互相访问.Session对象中止于联机机器离线时,也就是当网站使用者关掉浏览器或超过 ...
- Markdown的使用简介
以前有摘抄过,然而onenote速度感人,现在又主要用Linux,所以在这里备份一下,好方便用 Linux下推荐remakeble软件,或者直接sublime text,再或者vim,反正我不会ema ...
- HTML之:让网页中的<a>标签属性统一设置-如‘新窗口打开’
在开发过程中,我们往往想在页面中,给<a>设置一个统一的默认格式,例如我们想让链接:“在新窗口打开”,我们就可以使用<base>标签 在网页中添加这段代码: <head& ...
- 【Beta版本】冲刺计划及安排
目录 一.Beta的初步完善 二.团队分工的改进 三.工具流程的改进 四.冲刺阶段的计划与安排 五.关于组长是否重选 六.附录 队伍:606notconnected 成员:031401433 张斯巍 ...
- sublime text3 --前端工程师必备神器
sublime text3 --前端工程师必备神器 导读目录: 下载与Emmet插件安装 sublime text3 中cssrem安装与使用 sublime Text 3的中文文件名显示为方框的问题 ...
- EasyUi 方法传递多个参数值得方法
1.项目中需要传递多个参数值 function actionFtt(value, row, index) { //传递查询需要的参数 var customerId = row.customerId;/ ...
- 在Linux下安装和使用MySQL
[简 介] 想使用Linux已经很长时间了,由于没有硬性任务一直也没有系统学习,近日由于工作需要必须使用Linux下的MySQL.本以为有Windows下使用SQL Server的经验,觉得在Linu ...
- 自然语言6_treebank句子解析
#英文句子结构分析 import nltkfrom nltk.corpus import treebankt = treebank.parsed_sents('wsj_0001.mrg')[1]t.d ...
- JavaWeb学习笔记——Tomcat数据源
server.xml配置数据帐号和密码等
- BigDecimal类
如果需要精确的计算结果,则必须使用BigDecimal类,而且使用BigDecimal类也可以进行大数的操作. //========================================== ...
