[Reinforcement Learning] 动态规划(Planning)

动态规划

动态规划（Dynamic Programming，简称DP）是一种通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。

动态规划常常适用于具有如下性质的问题：

• 具有最优子结构（Optimal substructure）
  • Principle of optimality applies
  • Optimal solution can be decomposed into subproblems
• 重叠子问题（Overlapping subproblems）
  • Subproblems recur many times
  • Solutions can be cached and reused

动态规划方法所耗时间往往远少于朴素解法。

马尔可夫决策过程MDP满足上述两个性质：

• 贝尔曼方程提供了递归分解的结构；
• 价值函数可以保存和重复使用递归时的结果。

使用动态规划解决MDP/MRP

动态规划需要满足MDP过程是已知的（model-based）。

• For Predict：
  • Input：MDP \(<S, A, P, R, \gamma>\) 和策略 $\pi $ 或者是 MRP \(<S, P, R, \gamma>\)
  • Output：价值函数 \(v_{\pi}\)
• For Control：
  • Input：MDP \(<S, A, P, R, \gamma>\)
  • Output：最优价值函数 \(v_{*}\) 或者最优策略 \(\pi_{*}\)

策略评估

策略评估（Policy Evaluation）指的是计算给定策略的价值，解决的问题是 "How to evaluate a policy"。

策略评估的思路：迭代使用贝尔曼期望方程（关于 MDP 的贝尔曼期望方程形式见《马尔可夫决策过程》）。

策略评估过程如下图所示：

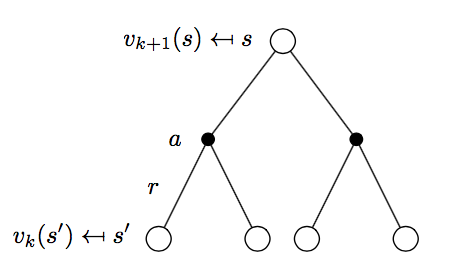
\[v_{k+1} = \sum_{a\in A}\pi(a|s) \Bigl( R_{s}^a + \gamma\sum_{s'\in S}P_{ss'}^a v_{k}(s') \Bigr)\]

使用向量形式表示：

\[\mathbf{v^{k+1}} = \mathbf{R^{\pi}} + \gamma \mathbf{P^{\pi}v^{k}}\]

策略迭代

策略迭代（Policy Iteration，简称PI）解决的问题是 "How to improve a policy"。

给定一个策略 \(\pi\)：

• 评估策略 \(\pi\)：
  \[v_{\pi}(s) = E[R_{t+1} + \gamma R_{t+2} + ...| S_t = s]\]
• 提升策略：通过采用贪婪方法来提升策略：
  \[\pi ' = \text{greedy}(v_{\pi})\]

可以证明，策略迭代不断进行总是能收敛到最优策略，即 \(\pi ' = \pi^{*}\)。

策略迭代可以使用下图来形式化的描述：

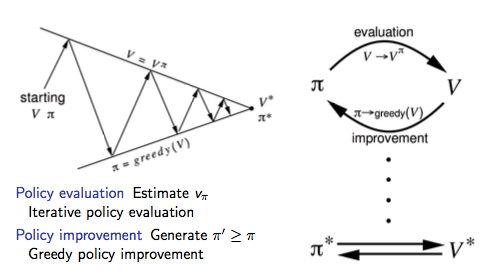
广义策略迭代

通过上述提到的策略评估我们不难发现，策略评估是一个不断迭代的过程：
\[v_{\pi}(s) = E[R_{t+1} + \gamma R_{t+2} + ...| S_t = s]\]

那么问题来了，Does policy evaluation need to converge to \(v_{\pi}\)?
我们是不是可以引入一个停止规则或者规定在迭代 \(k\) 次后停止策略评估？
再进一步想，我们为什么不在每次策略评估的迭代过程中进行策略提升（等同于策略评估迭代1次后停止）？
注：这和后续要介绍的值迭代等价。

因此我们可以把上述策略迭代的过程一般化，即广义策略迭代（Generalised Policy Iteration，简称GPI）框架：

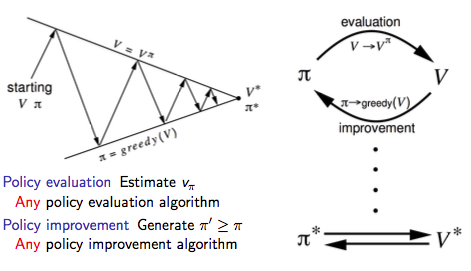
值迭代

介绍值迭代之前，我们先介绍下最优化原理。

最优化原理

最优化原理（Principle of Optimality）定义：

一个过程的最优决策具有这样的性质：即无论其初始状态和初始决策如何，其今后诸策略对以第一个决策所形成的状态作为初始状态的过程而言，必须构成最优策略。

最优化原理如果用数学化一点的语言来描述的话就是：

以状态 \(s\) 为起始点，策略 \(\pi(a|s)\) 可以得到最优值 \(v_{\pi}(s) = v_*(s)\) 当且仅当：

• 任意状态 \(s'\) 对于状态 \(s\) 均可达；
• 以状态 \(s'\) 为起始点，策略 \(\pi\) 可以得到最优值 \(v_{\pi}(s') = v_*(s')\)。

根据最优化原理可知，如果我们得到了子问题的解 $ v_*(s')$，那么以状态 \(s\) 为起始点的最优解 \(v_*(s)\) 可以通过一步回退（one-step lookahead）就能获取：
\[v_*(s) ← \max_{a\in A}\Bigl(R_s^a + \gamma \sum_{s'\in S}P_{ss'}^{a}v_*(s') \Bigr)\]

也就是说，我们可以从最后开始向前回退从而得到最优解，值迭代就是基于上述思想进行迭代更新的。

MDP值迭代

值迭代（Value Iteration，简称VI）解决的问题也是 "Find optimal policy $\pi $"。
但是不同于策略迭代使用贝尔曼期望方程的是，值迭代使用贝尔曼最优方程进行迭代提升。

值迭代与策略迭代不同的地方在于：

• Use Bellman optimal function, rather than Bellman expectation function
• Unlike policy iteration, there is no explicit policy
• Intermediate value functions may not correspond to any policy

如下图所示：

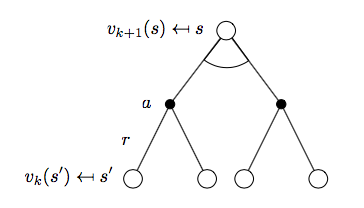
\[v_{k+1}(s) = \max_{a\in A}\Bigl(R_s^a + \gamma\sum_{s'\in S}P_{ss'}^a v_k(s') \Bigr)\]

对应的向量表示为：
\[\mathbf{v}_{k+1} = \max_{a\in A}\mathbf{R}^a + \gamma \mathbf{P^av}^k\]

下图为三种方法的总结：

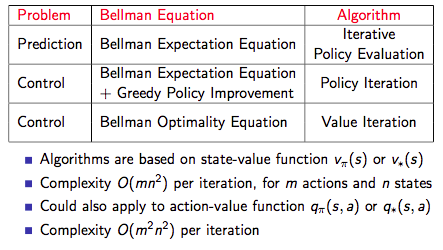
动态规划扩展

异步动态规划（Asynchronous Dynamic Programming）

• In-place dynamic programming
• Prioritised sweeping
• Real-time dynamic programming

Full-Width Backups vs. Sample Backups

Full-Width Backups

• DP uses full-width backups（DP is model-based）
  • Every successor state and action is considered
  • Using knowledge of the MDP transitions and reward function
• DP is effective for medium-sized problems (millions of states)
• For large problems, DP suffers Bellman’s curse of dimensionality（维度灾难）

维度灾难：Number of states \(n = |S|\) grows exponentially with number of state variables

• Even one backup can be too expensive

Sample Backups

后续将要讨论的时序差分方法

• Using sample rewards and sample transitions \(⟨S, A, R, S′⟩\)
• Instead of reward function R and transition dynamics P
• Advantages:
  • Model-free: no advance knowledge of MDP required
  • Breaks the curse of dimensionality through sampling
  • Cost of backup is constant, independent of \(n = |S|\)

Reference

[1] 智库百科-最优化原理
[2] Reinforcement Learning: An Introduction, Richard S. Sutton and Andrew G. Barto, 2018
[3] David Silver's Homepage