python 游戏 —— 汉诺塔(Hanoita)

python 游戏 —— 汉诺塔(Hanoita)

一、汉诺塔问题

1. 问题来源

　　问题源于印度的一个古老传说，大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

2. 问题阐述

　　塔内有三个座A、B、C，A座上有64个盘子，盘子从上到下逐渐变大，最下面的盘子最大。目前要把A座的64个盘子从A座移到C座，并且每次只能移动一个盘子，移动过程中三个座保持大盘子在下，小盘子在上，要求输出盘子的移动过程。

二、问题解析

1. 解决方法：递归方法

2. 解题过程

　　(1) 将上面63个盘子从A座移到B座

　　(2) 将最下面的盘子从A座移到C座

　　(3) 将B座的63个盘子从B座移到C座

三、问题解决

1. 非可视化解决

　　(1) 代码实现

 1 ''' 编程环境：python3.7  win7x64 '''
 2 def printf(A,C):  #盘子移动的输出格式
 3     print("{} --> {}".format(A,C))
 4
 5 def move(n,A,B,C):
 6     if n == 1:
 7         printf(A,C)     #将最后1个盘子从A座移到C座
 8     else:
 9         move(n-1,A,C,B) #将n个盘子从A座借助B座移到C座
10         printf(A,C)     #将最后1个盘子从A座移到C座
11         move(n-1,B,A,C) #将n个盘子从B座借助A座移到C座
12
13 N = int(input("请输入汉诺塔层数："))
14 move(N,'A','B','C')

　　　　(2) 有图有真相

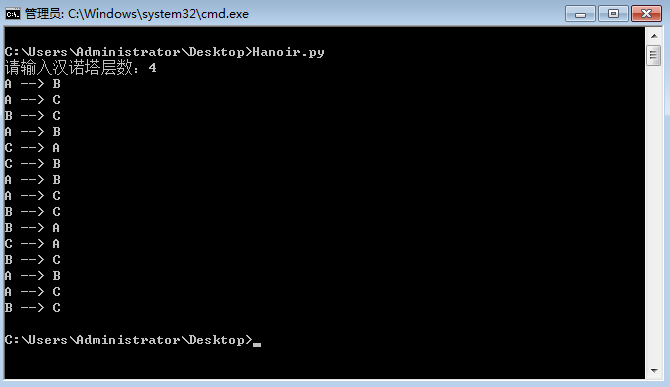
2. 可视化解决

　　(1) 代码实现

 1 ''' 编程环境：python3.7  win7x64 '''
 2 from turtle import *
 3 class Stack:
 4     def __init__(self):
 5         self.items = []
 6     def isEmpty(self):
 7         return len(self.items) == 0
 8     def push(self, item):
 9         self.items.append(item)
10     def pop(self):
11         return self.items.pop()
12     def peek(self):
13         if not self.isEmpty():
14             return self.items[len(self.items) - 1]
15     def size(self):
16         return len(self.items)
17
18 def drawpole_1(k):#画汉诺塔的底座
19     up()
20     pensize(10)
21     speed(100)
22     goto(400*(k-1), 100)
23     down()
24     goto(400*(k-1), -100)
25     goto(400*(k-1)-20, -100)
26     goto(400*(k-1)+20, -100)
27
28 def drawpole_3():#画出汉诺塔的三个底座
29     hideturtle()#隐藏
30     drawpole_1(0)#画出汉诺塔的底座左
31     drawpole_1(1)#画出汉诺塔的底座中
32     drawpole_1(2)#画出汉诺塔的底座右
33
34 def creat_plates(n):#制造n个盘子
35     plates=[Turtle() for i in range(n)]
36     for i in range(n):
37         plates[i].up()
38         plates[i].hideturtle()
39         plates[i].shape("square")
40         plates[i].shapesize(1,8-i)
41         plates[i].goto(-400,-90+20*i)
42         plates[i].showturtle()
43     return plates
44
45 def pole_stack():#制造底座的栈
46     poles=[Stack() for i in range(3)]
47     return poles
48
49 def moveDisk(plates,poles,fp,tp):#把poles[fp]顶端的盘子plates[mov]从poles[fp]移到poles[tp]
50     mov=poles[fp].peek()
51     plates[mov].goto((fp-1)*400,150)
52     plates[mov].goto((tp-1)*400,150)
53     l=poles[tp].size()#确定移动到底部的高度（恰好放在原来最上面的盘子上面）
54     plates[mov].goto((tp-1)*400,-90+20*l)
55
56 def moveTower(plates,poles,height,fromPole, toPole, withPole):#递归放盘子
57     if height >= 1:
58         moveTower(plates,poles,height-1,fromPole,withPole,toPole)
59         moveDisk(plates,poles,fromPole,toPole)
60         poles[toPole].push(poles[fromPole].pop())
61         moveTower(plates,poles,height-1,withPole,toPole,fromPole)
62
63 myscreen=Screen()
64 setup(1200,500) #设置窗口大小
65 drawpole_3()    #画汉诺塔的底座
66 n=int(input("请输入汉诺塔的层数并回车:"))#输入汉诺塔的盘子数
67 plates=creat_plates(n)#制造n个盘子
68 poles=pole_stack()
69 for i in range(n):
70     poles[0].push(i)
71 moveTower(plates,poles,n,0,2,1)
72 myscreen.exitonclick()

　　(2) 有图有真相