BUAA-OO-第一单元表达式求导作业总结

figure:first-child { margin-top: -20px; }
#write ol, #write ul { position: relative; }
img { max-width: 100%; vertical-align: middle; }
button, input, select, textarea { color: inherit; font-style: inherit; font-variant: inherit; font-weight: inherit; font-stretch: inherit; font-size: inherit; line-height: inherit; font-family: inherit; }
input[type="checkbox"], input[type="radio"] { line-height: normal; padding: 0px; }
*, ::after, ::before { box-sizing: border-box; }
#write h1, #write h2, #write h3, #write h4, #write h5, #write h6, #write p, #write pre { width: inherit; }
#write h1, #write h2, #write h3, #write h4, #write h5, #write h6, #write p { position: relative; }
h1, h2, h3, h4, h5, h6 { break-after: avoid-page; break-inside: avoid; orphans: 2; }
p { orphans: 4; }
h1 { font-size: 2rem; }
h2 { font-size: 1.8rem; }
h3 { font-size: 1.6rem; }
h4 { font-size: 1.4rem; }
h5 { font-size: 1.2rem; }
h6 { font-size: 1rem; }
.md-math-block, .md-rawblock, h1, h2, h3, h4, h5, h6, p { margin-top: 1rem; margin-bottom: 1rem; }
.hidden { display: none; }
.md-blockmeta { color: rgb(204, 204, 204); font-weight: 700; font-style: italic; }
a { cursor: pointer; }
sup.md-footnote { padding: 2px 4px; background-color: rgba(238, 238, 238, 0.7); color: rgb(85, 85, 85); border-radius: 4px; cursor: pointer; }
sup.md-footnote a, sup.md-footnote a:hover { color: inherit; text-transform: inherit; text-decoration: inherit; }
#write input[type="checkbox"] { cursor: pointer; width: inherit; height: inherit; }
figure { overflow-x: auto; margin: 1.2em 0px; max-width: calc(100% + 16px); padding: 0px; }
figure > table { margin: 0px !important; }
tr { break-inside: avoid; break-after: auto; }
thead { display: table-header-group; }
table { border-collapse: collapse; border-spacing: 0px; width: 100%; overflow: auto; break-inside: auto; text-align: left; }
table.md-table td { min-width: 32px; }
.CodeMirror-gutters { border-right: 0px; background-color: inherit; }
.CodeMirror-linenumber { user-select: none; }
.CodeMirror { text-align: left; }
.CodeMirror-placeholder { opacity: 0.3; }
.CodeMirror pre { padding: 0px 4px; }
.CodeMirror-lines { padding: 0px; }
div.hr:focus { cursor: none; }
#write pre { white-space: pre-wrap; }
#write.fences-no-line-wrapping pre { white-space: pre; }
#write pre.ty-contain-cm { white-space: normal; }
.CodeMirror-gutters { margin-right: 4px; }
.md-fences { font-size: 0.9rem; display: block; break-inside: avoid; text-align: left; overflow: visible; white-space: pre; background: inherit; position: relative !important; }
.md-diagram-panel { width: 100%; margin-top: 10px; text-align: center; padding-top: 0px; padding-bottom: 8px; overflow-x: auto; }
#write .md-fences.mock-cm { white-space: pre-wrap; }
.md-fences.md-fences-with-lineno { padding-left: 0px; }
#write.fences-no-line-wrapping .md-fences.mock-cm { white-space: pre; overflow-x: auto; }
.md-fences.mock-cm.md-fences-with-lineno { padding-left: 8px; }
.CodeMirror-line, twitterwidget { break-inside: avoid; }
.footnotes { opacity: 0.8; font-size: 0.9rem; margin-top: 1em; margin-bottom: 1em; }
.footnotes + .footnotes { margin-top: 0px; }
.md-reset { margin: 0px; padding: 0px; border: 0px; outline: 0px; vertical-align: top; background: 0px 0px; text-decoration: none; text-shadow: none; float: none; position: static; width: auto; height: auto; white-space: nowrap; cursor: inherit; -webkit-tap-highlight-color: transparent; line-height: normal; font-weight: 400; text-align: left; box-sizing: content-box; direction: ltr; }
li div { padding-top: 0px; }
blockquote { margin: 1rem 0px; }
li .mathjax-block, li p { margin: 0.5rem 0px; }
li { margin: 0px; position: relative; }
blockquote > :last-child { margin-bottom: 0px; }
blockquote > :first-child, li > :first-child { margin-top: 0px; }
.footnotes-area { color: rgb(136, 136, 136); margin-top: 0.714rem; padding-bottom: 0.143rem; white-space: normal; }
#write .footnote-line { white-space: pre-wrap; }
@media print {
body, html { border: 1px solid transparent; height: 99%; break-after: avoid; break-before: avoid; }
#write { margin-top: 0px; padding-top: 0px; border-color: transparent !important; }
.typora-export * { -webkit-print-color-adjust: exact; }
html.blink-to-pdf { font-size: 13px; }
.typora-export #write { padding-left: 32px; padding-right: 32px; padding-bottom: 0px; break-after: avoid; }
.typora-export #write::after { height: 0px; }
@page { margin: 20mm 0px; }
}
.footnote-line { margin-top: 0.714em; font-size: 0.7em; }
a img, img a { cursor: pointer; }
pre.md-meta-block { font-size: 0.8rem; min-height: 0.8rem; white-space: pre-wrap; background: rgb(204, 204, 204); display: block; overflow-x: hidden; }
p > .md-image:only-child:not(.md-img-error) img, p > img:only-child { display: block; margin: auto; }
p > .md-image:only-child { display: inline-block; width: 100%; }
#write .MathJax_Display { margin: 0.8em 0px 0px; }
.md-math-block { width: 100%; }
.md-math-block:not(:empty)::after { display: none; }
[contenteditable="true"]:active, [contenteditable="true"]:focus { outline: 0px; box-shadow: none; }
.md-task-list-item { position: relative; list-style-type: none; }
.task-list-item.md-task-list-item { padding-left: 0px; }
.md-task-list-item > input { position: absolute; top: 0px; left: 0px; margin-left: -1.2em; margin-top: calc(1em - 10px); border: none; }
.math { font-size: 1rem; }
.md-toc { min-height: 3.58rem; position: relative; font-size: 0.9rem; border-radius: 10px; }
.md-toc-content { position: relative; margin-left: 0px; }
.md-toc-content::after, .md-toc::after { display: none; }
.md-toc-item { display: block; color: rgb(65, 131, 196); }
.md-toc-item a { text-decoration: none; }
.md-toc-inner:hover { text-decoration: underline; }
.md-toc-inner { display: inline-block; cursor: pointer; }
.md-toc-h1 .md-toc-inner { margin-left: 0px; font-weight: 700; }
.md-toc-h2 .md-toc-inner { margin-left: 2em; }
.md-toc-h3 .md-toc-inner { margin-left: 4em; }
.md-toc-h4 .md-toc-inner { margin-left: 6em; }
.md-toc-h5 .md-toc-inner { margin-left: 8em; }
.md-toc-h6 .md-toc-inner { margin-left: 10em; }
@media screen and (max-width: 48em) {
.md-toc-h3 .md-toc-inner { margin-left: 3.5em; }
.md-toc-h4 .md-toc-inner { margin-left: 5em; }
.md-toc-h5 .md-toc-inner { margin-left: 6.5em; }
.md-toc-h6 .md-toc-inner { margin-left: 8em; }
}
a.md-toc-inner { font-size: inherit; font-style: inherit; font-weight: inherit; line-height: inherit; }
.footnote-line a:not(.reversefootnote) { color: inherit; }
.md-attr { display: none; }
.md-fn-count::after { content: "."; }
code, pre, samp, tt { font-family: var(--monospace); }
kbd { margin: 0px 0.1em; padding: 0.1em 0.6em; font-size: 0.8em; color: rgb(36, 39, 41); background: rgb(255, 255, 255); border: 1px solid rgb(173, 179, 185); border-radius: 3px; box-shadow: rgba(12, 13, 14, 0.2) 0px 1px 0px, rgb(255, 255, 255) 0px 0px 0px 2px inset; white-space: nowrap; vertical-align: middle; }
.md-comment { color: rgb(162, 127, 3); opacity: 0.8; font-family: var(--monospace); }
code { text-align: left; vertical-align: initial; }
a.md-print-anchor { white-space: pre !important; border-width: initial !important; border-style: none !important; border-color: initial !important; display: inline-block !important; position: absolute !important; width: 1px !important; right: 0px !important; outline: 0px !important; background: 0px 0px !important; text-decoration: initial !important; text-shadow: initial !important; }
.md-inline-math .MathJax_SVG .noError { display: none !important; }
.html-for-mac .inline-math-svg .MathJax_SVG { vertical-align: 0.2px; }
.md-math-block .MathJax_SVG_Display { text-align: center; margin: 0px; position: relative; text-indent: 0px; max-width: none; max-height: none; min-height: 0px; min-width: 100%; width: auto; overflow-y: hidden; display: block !important; }
.MathJax_SVG_Display, .md-inline-math .MathJax_SVG_Display { width: auto; margin: inherit; display: inline-block !important; }
.MathJax_SVG .MJX-monospace { font-family: var(--monospace); }
.MathJax_SVG .MJX-sans-serif { font-family: sans-serif; }
.MathJax_SVG { display: inline; font-style: normal; font-weight: 400; line-height: normal; zoom: 90%; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; padding: 0px; margin: 0px; }
.MathJax_SVG * { transition: none; }
.MathJax_SVG_Display svg { vertical-align: middle !important; margin-bottom: 0px !important; }
.os-windows.monocolor-emoji .md-emoji { font-family: "Segoe UI Symbol", sans-serif; }
.md-diagram-panel > svg { max-width: 100%; }
[lang="mermaid"] svg, [lang="flow"] svg { max-width: 100%; }
[lang="mermaid"] .node text { font-size: 1rem; }
table tr th { border-bottom: 0px; }
video { max-width: 100%; display: block; margin: 0px auto; }
iframe { max-width: 100%; width: 100%; border: none; }
.highlight td, .highlight tr { border: 0px; }

.typora-export li, .typora-export p, .typora-export, .footnote-line {white-space: normal;}
-->

第一单元表达式求导作业

写在前面

本学期接触OOP面向对象编程这门课程，三周以来，第一单元的作业（表达式求导）已经基本完成，在此过程中，我初次接触到面向对象的思想，锻炼使用这种思想来编程解决一些问题；互测屋这种新的测评方式，也让人感触良多。

第一单元的作业围绕表达式求导，进行了三次逐渐扩展，难度递增的project，下面我将介绍在三次作业中的思路与代码架构，以及一些想法。再根据Metrics度量来分析我的程序架构。然后我将反思我程序的bug和互测屋测试别人的bug，最后思考重构方案，并总结心得体会。

一、设计思路与架构

Project 1 幂函数多项式求导

第一次作业可以说比较简单，在之前C语言的学习中，我们曾用结构体与链表实现过。可以说思路非常简单。

但不同的是，我们需要解析字符串，构建表达式，并且进行有效性的判断，如果输入表达式非法，需要输出WRONG FORMAT!

对于有效性判断，我练习使用了正则表达式。但是考虑到1000 char的要求，如果全部匹配，会发生爆栈。所以我通过循环匹配每一项，然后再从式中剪切掉，判断能否得到空串来判断有效性。

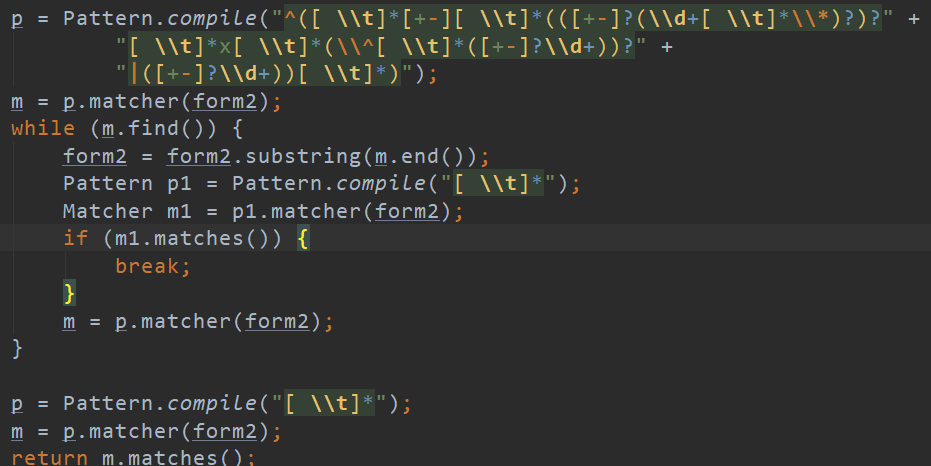
解析表达式，我使用正则，配合使用Pattern和Matcher，通过不同的捕获组进行表达式的解析。

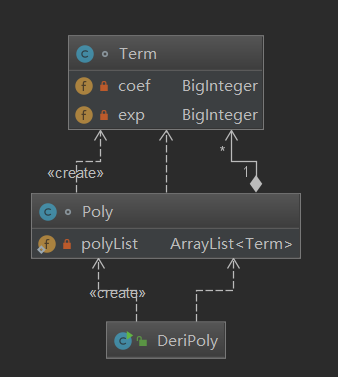
第一次的作业代码架构，我建立了一个Term类，具有coef（系数）和exp（指数）的成员变量来表示每一个项，并再Poly类使用了ArrayList<Term>来存储表达式的每一项。

定义了Deri（求导）和print（输出）函数来实现求导和输出的功能。由于性能要求表达式尽可能短，所以再Poly中定义了simplify方法，循环对合并同类像对表达式进行化简。

UML第一次作业的构架如下图所示：

Project 2 幂函数与三角函数混合表达式求导

第一次作业中，我还没有什么面向对象编程的思想，写的非常面向过程，结构也没有可扩展性，导致了第二次作业完全重写的情况.......

第二次作业我重写了代码结构，为了尽可能的让程序具有扩展性，以便为第三次作业进行准备。

我建立了Expr（表达式）、Term（项）和Factor（因子）三级结构。其中Factor为抽象类，Power（幂函数），Sin（正弦函数），Cos（余弦函数）三个基本函数继承抽象类Factor。在Expr建立ArrayList<Term>，在Term中建立ArrayList<Factor>来实现三级存储。其结构如下图：

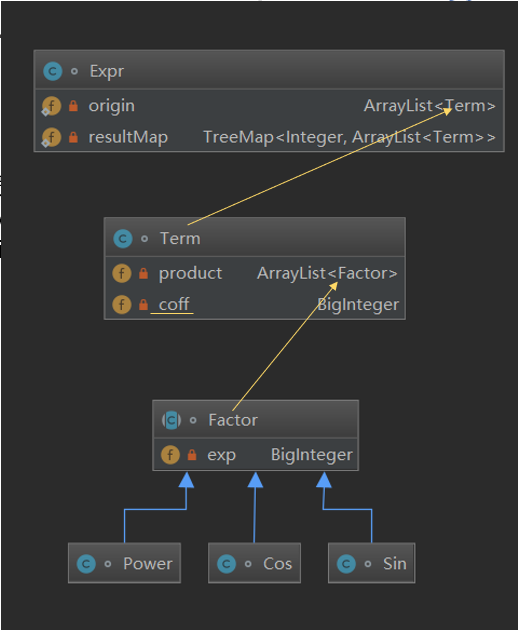
有效性判断依旧使用正则表达式，判断后化简，去除空白字符，处理连续的加减号。

解析表达式使用Pattern & matcher ，在解析时统一结构合并为 A * x^B * sin(x)^C * cos(x)^D，并且固定三个基本因子在ArrayList中的位置，这个合并可以简化求导时的计算。

求导时逐级遍历求导，A*B x^(B-1) * sin(x)^C * cos(x)^D，A*C x^B * sin(x)^(C-1) * cos(x)^(D+1)，A*D x^B * sin(x)^(C+1) * cos(x)^(D-1)

在本单元的化简中，我是用了启发式的化简方法，是一个很好的思路。

启发式化简

启发式思想

一个基于直观或经验构造的算法，在可接受的花费（指计算时间和空间）下给出待解决组合优化问题每一个实例的一个可行解。

直观或经验构造的算法：sin(x)^2 + cos(x)^2= 1

可接受的花费：最大允许CPU时间1秒

每一个实例的一个可行解：记录每一个解的长度及其表达式，选择最优解（最短）输出。

所以，我用使用TreeMap结构存储，因为其有序性，方便直接取得最优解。

化简的流程为：

（1）随机选择，从TreeMap中随机选择一个表达式，再随机选择表达式中一项开始遍历，如有某项sin(x)因子的指数≥2，将其中的sin(x)\^2变为1-cos(x)\^2，然后调用基本化简，循环此操作。

（2）基本化简，从头遍历表达式各项（双循环）将A * sin(x)\^2 + A * cos(x)\^2化简为A

(3)限定条件，（循环次数或循环）输出得到的最优解，TreeMap. get(TreeMap.firstKey)。

具体代码如下：

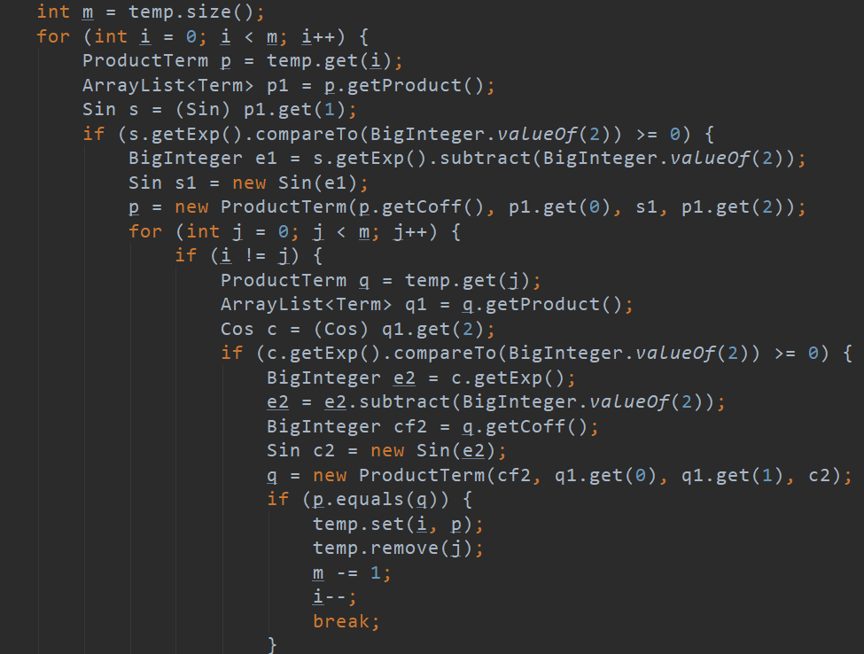
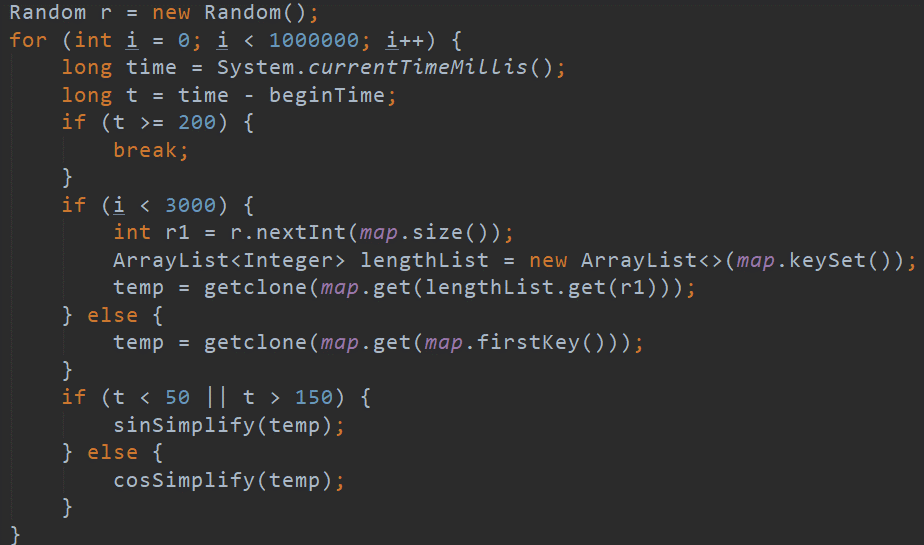
总体来说，启发式化简思路简单，易于操作，只有sin(x)\^2+cos(x)\^2=1，这一条语法规则。其不断循环也可以处理高次方的化简问题。其可将表达式化简到最简。很多商业软件就是用的启发式算法进行化简，如Project 3评测采用的sympy。但是随机具有的不确定性，让此方法有些风险。如评测机不稳定等原因造成的TLE，对与统一式子化简得到如果有足够的时间，结果每次不一样等等。

Project 3 包含幂函数，三角函数，项嵌套的表达式求导

第三次作业在第二次作业中增加了嵌套，我在我第二次作业的基础上进行了扩展，增加了Digit（常数因子）和ExpFactor（表达式因子）继承抽象类Factor，增加了递归以实现了嵌套。其框架结构如下图所示：

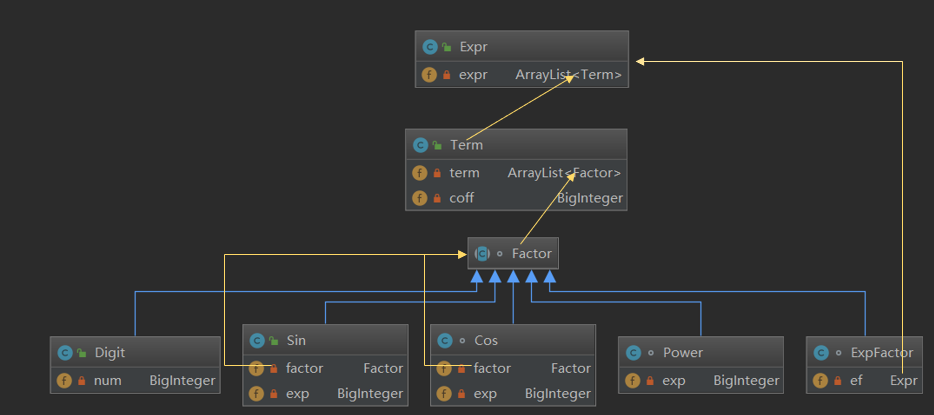
由于此次的递归，无法使用正则表达式匹配，所以我学习使用了递归下降来进行表达式有效性判断和解析 。我新建表达式解析类，在其中共享数据流，并且新建每一个类对应的方法，返回值式每一个对应的类，表达式因子和三角函数括号内的因子需要将进行递归调用。

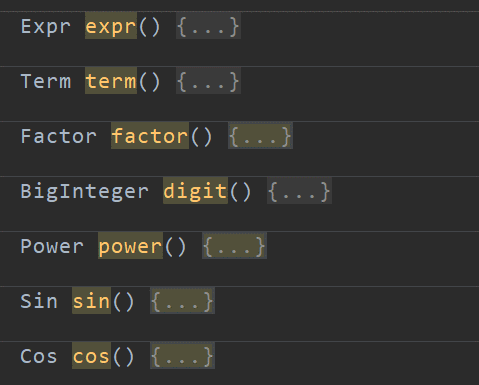
由于构架，求导也需要递归，并且各级求导返回都返回表达式(Expr)，并且要定义表达式的加法与乘法。

对于化简，要进行去括号和合并等操作，都需要递归进行，并且改变存储结构。

二、基于Metrics度量分析程序结构

使用Metrics来对面向对象程序进行度量是非常重要的。对于Project 1和Project 2 来说，由于代码结构比较简单，所以Metrics度量问题显示的不够明显。到Project 3时，我代码的问题暴露的非常冥想。下面我主要对我第三次作业代码进行Metrics度量的分析。

1、基于CK标准度量

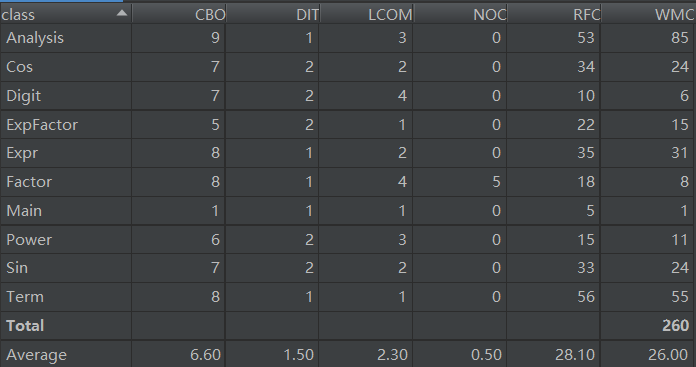
（1）CBO 对象类之间的耦合

Metrics测试显示我代码大部分类的耦合度在7及以上，代码的耦合度还是比较高的，这会对代码的复用性造成影响。

（2）DIT与NOC

从这两项指标可以看出，我的代码深度及继承度都不足。由于初始面向对象，我的思想还比较浅显，代码构架的设计非常简单。虽然也成功解决了问题，但是代码的可扩展性不足。如果本单元还需要继续扩展，我的构架可能难以支持，这是我今后在写码前的设计过程中必须要考虑的。

（3）WMC 加权方法数

从测试中可以看出，我的有些类（如Analysis）的WMC值是非常高的，这是我从面向过程编程带来的问题，习惯吧一整套流程写在一个类中，导致有些类的加权方法数很大，这样会影响代码的通用性和复用性。

（4）RFC 类的响应集的大小

我的代码在此项数据中也有着较高的数值，类中方法被调用的过多，让代码调试变得困难。

2、对方法复杂对的分析

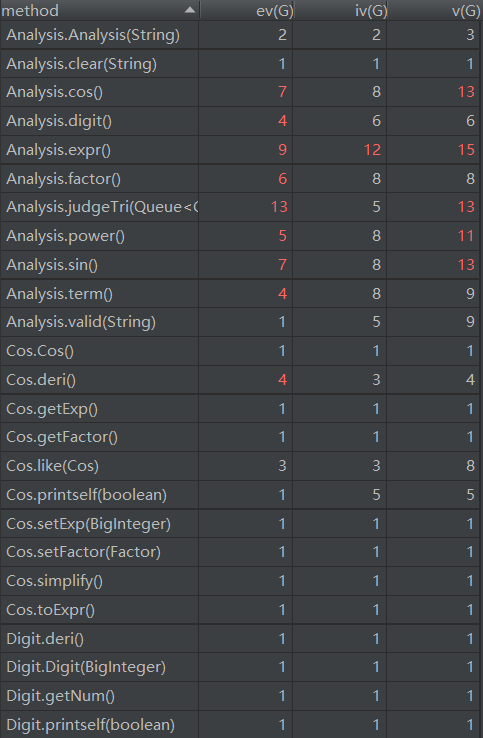
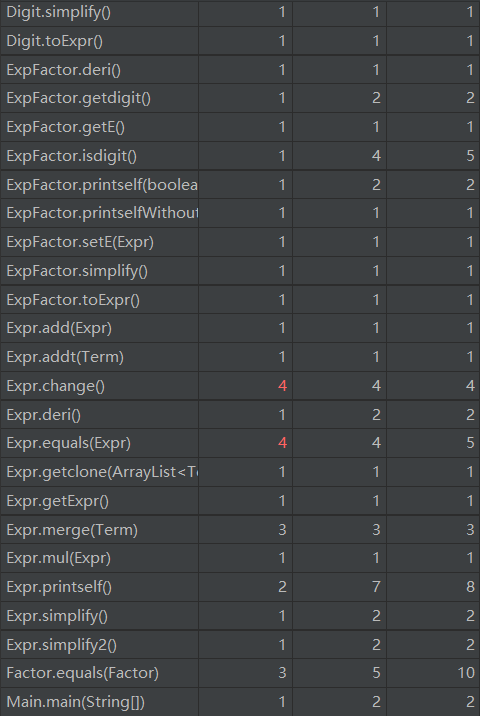
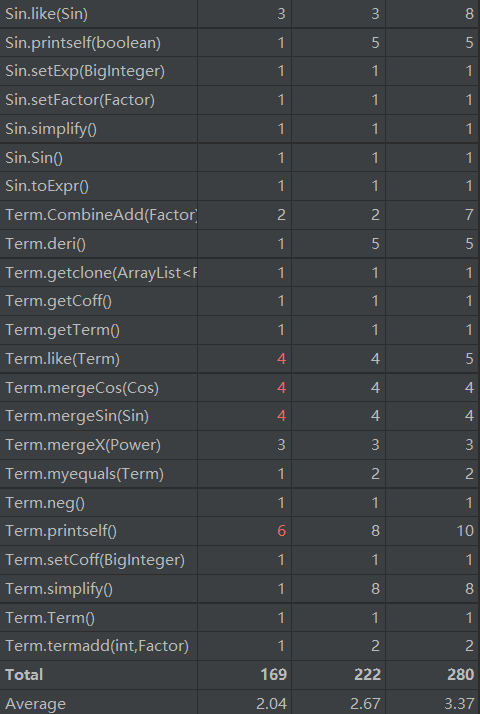
通过对方法复杂度的分析可以看出，Analysis类中的方法，复杂度非常高。这是由于我的主要功能与流程都集中在了此类中。这是一种不好的风格，影响了代码的复用性和扩展性，增加了出错的概率和调试的难度。

三、我的bug（悲剧啊.......

可以所在三次作业中，我的粗心和测试不足，让我付出了非常大的代价。

在第一次作业测试中，在输出的方法中，我对 -1*x 形式的量输出的时候会输出 -*x 的导致公测和互测频繁被爆。

在第二次作业测试中，由于我在解析表达式的时候，把正负号相连情况化为一个符号，但是其中存在-+-的情况化为了-号（应为+号），公测没有被测出，但导致互测被