【模式匹配】更快的Boyer-Moore算法

1. 引言

前一篇中介绍了字符串KMP算法，其利用失配时已匹配的字符信息，以确定下一次匹配时模式串的起始位置。本文所要介绍的Boyer-Moore算法是一种比KMP更快的字符串匹配算法，它到底是怎么快的呢？且听下面分解。

不同于KMP在匹配过程中从左至右与主串字符做比较，Boyer-Moore算法是从模式串的尾字符开始从右至左做比较。下面讨论的一些递推式都与BM算法的这个特性有关。

思想

首先，我们一般化匹配失败的情况，设主串\(y\)、模式串\(x\)的失配位置为i+j与i，且主串、模式串的长度各为\(n\)与\(m\)，如下图：

已匹配上的字符结构：

\[y[i+j+1 \dots j+m-1] = x[i+1 \dots m-1]
\]

失配后下一次匹配时，模式串应如何对齐于主串呢？从上图中看出，我们可以利用两方面的信息：

1. 已经匹配上的字符结构，
2. 主串失配位置的字符

前一篇中的KMP算法只利用第一条信息，而Boyer-Moore算法则是将这两方面的信息都利用到了，故模式串的移动更为高效。同时，根据这两方面信息（已匹配信息与失配信息），Boyer-Moore算法引申出来两条移动规则：好后缀移动（good-suffix shift）与坏字符移动（bad-character shift）。

实例

Moore教授在这里给出BM算法一个实例，比如主串=HERE IS A SIMPLE EXAMPLE ，模式串=EXAMPLE。第一次匹配如下图：

在第一次匹配中，模式串在尾字符发生失配，而主串的失配字符为S，且S不属于模式串的字符；因此下一次匹配时模式串指针应向右移动7位（坏字符移动）。第二次匹配如下图：

第二次匹配也是在模式串尾字符发生失配，但不同的是主串的失配字符为P属于模式串的字符；因此下一次匹配时模式串的P（从右开始第一次出现）应对齐于主串的失配字符P（坏字符移动）。第三次匹配如下图：

在第三次匹配中，模式串的后缀MPLE完全匹配上主串，主串的失配字符为I，不属于模式串的字符；那么下一次匹配是模式串指针应怎么移动呢（是坏字符移动，还是好后缀移动？）？BM算法采取的办法：移动步数=\(\max\{坏字符移动步数,\ 好后缀移动步数\}\)。（具体移动步数的计算会在下面给出），这里是按好后缀移动；第四次匹配如下图：

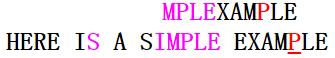
第四次匹配的情况与第二次类似，应按坏字符移动，第五次匹配（模式串与主串完全匹配）如下图：

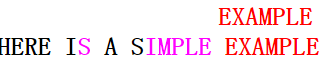
2. BM算法详述

好后缀移动

因已匹配上的字符结构正好为模式串的后缀，故名之为好后缀。好后缀移动一般分为两种情况：

1. 移动后，模式串有子串能完全匹配上好后缀；
2. 移动后，模式串只有能部分匹配上好后缀的子串

我们用数组bmGs[i]表示模式串的失配位置为i时好后缀移动的步数。第一类情况如下图：

第二类情况如下图：

接下来的问题是应如何计算bmGs[i]呢？我们引入suff函数，其定义如下：

\[suff[i]=\max \{k:\ x[i-k+1\dots i]=x[m-k\dots m-1\},1\le i < m
\]

表示了模式串中末字符为x[i]的子串能匹配模式串后缀的最大长度。其中，suff[i]=m。

• 对于第一类情况，令i+1=m-suff[a]，则x[i+1..m-1]=x[m-suff[a]..m-1]；根据suff函数的定义，有x[m-suff[a]..m-1]=x[a-suff[a]-1..a]；则x[i+1..m-1]=x[a-suff[a]-1..a]，即可得到bmGs[i]=bmGs[m-suff[a]-1]=m-1-a。

• 对于第二类情况，由字符的部分匹配可得x[0..m-1-bmGs[i]]=x[bmGs[i]..m-1]，即suff[m-1-bmGs[i]]=m-bmGs[i]。令m-bmGs[i]=a，有suff[a-1]=a。因为是部分匹配，故bmGs[i] = m-a > i+1，则i < m-a-1。综上，当i < m-a-1且suff[a-1]=a时，bmGs[i]=m-a。

• 有可能上述两种情况都没能被匹配上，则bmGs[i]=m。

综合上述三类情况，bmGs数组计算的实现代码（参看[2]）：

void preBmGs(char *x, int m, int bmGs[]) {
   int i, j, suff[XSIZE];

   suffixes(x, m, suff);

   // case 3, default value
   for (i = 0; i < m; ++i)
      bmGs[i] = m;
   j = 0;
   // case 2
   for (i = m - 1; i >= 0; --i)
      if (suff[i] == i + 1)
         for (; j < m - 1 - i; ++j)
            if (bmGs[j] == m)
               bmGs[j] = m - 1 - i;
   // case 1
   for (i = 0; i <= m - 2; ++i)
      bmGs[m - 1 - suff[i]] = m - 1 - i;
}

坏字符移动

坏字符移动是根据主串失配位置的字符y[i+j]而进行的移动。同样地，我们用数组bmBc[c]表示主串失配位置字符为c时坏字符移动的步数。坏字符移动一般分为两种情况：

1. 模式串x[0..i-1]有字符y[i+j]且第一次出现，如下图：
   
   

2. 整个模式串都不包含该字符串，如下图：
   
   

据此，可以将bmBc[c]定义如下：

\[bmBc[c]=\min \{i: 1\le i < m \ and \ x[m-1-i]=c \}
\]

表示距模式串末字符最近的c字符；若c字符未出现在模式串中，则bmBc[c]=m。C实现代码：

void preBmBc(char *x, int m, int bmBc[]) {
   int i;

   for (i = 0; i < ASIZE; ++i)
      bmBc[i] = m;
   for (i = 0; i < m - 1; ++i)
      bmBc[x[i]] = m - i - 1;
}

suff函数计算

bmGs[i]的计算依赖于suff函数；如何更为高效的计算suff函数成为了接下来需要考虑的问题。符号标记的定义如下：

• i表示当前位置；
• f记录上一轮匹配的起始位置；
• g记录上一轮匹配的失配位置。

这里所说的匹配指的是与模式串后缀的匹配。同样地，一般化匹配过程，如下图：

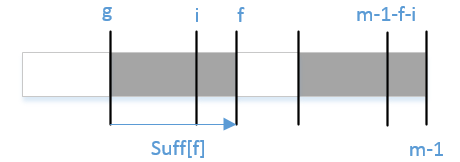
当g < i < f则必有x[i]=x[m-1-(f-i)]=x[m-1-f+i]；

• 若suff[m-1-f+i] < i-g，则suff[i]=suff[m-1-f+i]；
• 否则，suff[i]与suff[m-1-f+i]没有关系，要根据定义进行计算。

C实现代码：

void suffixes(char *x, int m, int *suff) {
   int f, g, i;

   suff[m - 1] = m;
   g = m - 1;
   for (i = m - 2; i >= 0; --i) {
      if (i > g && suff[i + m - 1 - f] < i - g)
         suff[i] = suff[i + m - 1 - f];
      else {
         if (i < g)
            g = i;
         f = i;
         while (g >= 0 && x[g] == x[g + m - 1 - f])
            --g;
         suff[i] = f - g;
      }
   }
}

复杂度分析

3. 参考资料

[1] Moore, Boyer-Moore algorithm example.

[2] Thierry Lecroq, Boyer-Moore algorithm.

[3] sealyao, Boyer-Moore算法学习.