[Unity A*算法]A*算法的简单实现

写在前面：之前看过一点，然后看不懂，也没用过。

最近正好重构项目看到寻路这块，想起来就去查查资料，总算稍微理解一点了，下面记录一下自己的成果（哈哈哈 :> ）

下面分享几篇我觉得挺不错的文章

A*算法

A*寻路算法详细解读

========================================================================================

搜索区域(The Search Area)

我们假设某人要从 A 点移动到 B 点，但是这两点之间被一堵墙隔开。如图 1 ，绿色是 A ，红色是 B ，中间蓝色是墙。

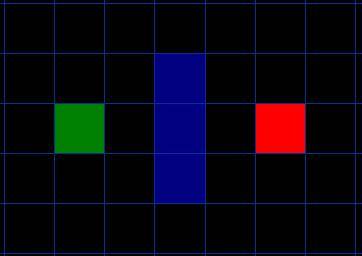
图 1

你应该注意到了，我们把要搜寻的区域划分成了正方形的格子。这是寻路的第一步，简化搜索区域，就像我们这里做的一样。这个特殊的方法把我们的搜索区域简化为了 2 维数组。数组的每一项代表一个格子，它的状态就是可走 (walkalbe) 和不可走 (unwalkable) 。通过计算出从 A 到 B需要走过哪些方格，就找到了路径。一旦路径找到了，人物便从一个方格的中心移动到另一个方格的中心，直至到达目的地。

方格的中心点我们成为“节点 (nodes) ”。如果你读过其他关于 A* 寻路算法的文章，你会发现人们常常都在讨论节点。为什么不直接描述为方格呢？因为我们有可能把搜索区域划为为其他多变形而不是正方形，例如可以是六边形，矩形，甚至可以是任意多变形。而节点可以放在任意多边形里面，可以放在多变形的中心，也可以放在多边形的边上。我们使用这个系统，因为它最简单。

开始搜索(Starting the Search)

一旦我们把搜寻区域简化为一组可以量化的节点后，就像上面做的一样，我们下一步要做的便是查找最短路径。在 A* 中，我们从起点开始，检查其相邻的方格，然后向四周扩展，直至找到目标。

我们这样开始我们的寻路旅途：

1.       从起点 A 开始，并把它就加入到一个由方格组成的 open list( 开放列表 ) 中。这个 open list 有点像是一个购物单。当然现在 open list 里只有一项，它就是起点 A ，后面会慢慢加入更多的项。 Open list 里的格子是路径可能会是沿途经过的，也有可能不经过。基本上 open list 是一个待检查的方格列表。

2.       查看与起点 A 相邻的方格 ( 忽略其中墙壁所占领的方格，河流所占领的方格及其他非法地形占领的方格 ) ，把其中可走的 (walkable) 或可到达的 (reachable) 方格也加入到 open list 中。把起点 A 设置为这些方格的父亲 (parent node 或 parent square) 。当我们在追踪路径时，这些父节点的内容是很重要的。稍后解释。

3.       把 A 从 open list 中移除，加入到 close list( 封闭列表 ) 中， close list 中的每个方格都是现在不需要再关注的。

如下图所示，深绿色的方格为起点，它的外框是亮蓝色，表示该方格被加入到了 close list 。与它相邻的黑色方格是需要被检查的，他们的外框是亮绿色。每个黑方格都有一个灰色的指针指向他们的父节点，这里是起点 A 。

图 2 。

下一步，我们需要从 open list 中选一个与起点 A 相邻的方格，按下面描述的一样或多或少的重复前面的步骤。但是到底选择哪个方格好呢？具有最小 F 值的那个。

路径排序(Path Sorting)

计算出组成路径的方格的关键是下面这个等式：

F = G + H

这里，

G = 从起点 A 移动到指定方格的移动代价，沿着到达该方格而生成的路径。

H = 从指定的方格移动到终点 B 的估算成本。这个通常被称为试探法，有点让人混淆。为什么这么叫呢，因为这是个猜测。直到我们找到了路径我们才会知道真正的距离，因为途中有各种各样的东西 ( 比如墙壁，水等 ) 。本教程将教你一种计算 H 的方法，你也可以在网上找到其他方法。

我们的路径是这么产生的：反复遍历 open list ，选择 F 值最小的方格。这个过程稍后详细描述。我们还是先看看怎么去计算上面的等式。

如上所述， G 是从起点Ａ移动到指定方格的移动代价。在本例中，横向和纵向的移动代价为 10 ，对角线的移动代价为 14 。之所以使用这些数据，是因为实际的对角移动距离是 2 的平方根，或者是近似的 1.414 倍的横向或纵向移动代价。使用 10 和 14 就是为了简单起见。比例是对的，我们避免了开放和小数的计算。这并不是我们没有这个能力或是不喜欢数学。使用这些数字也可以使计算机更快。稍后你便会发现，如果不使用这些技巧，寻路算法将很慢。

既然我们是沿着到达指定方格的路径来计算 G 值，那么计算出该方格的 G 值的方法就是找出其父亲的 G 值，然后按父亲是直线方向还是斜线方向加上 10 或 14 。随着我们离开起点而得到更多的方格，这个方法会变得更加明朗。

有很多方法可以估算 H 值。这里我们使用 Manhattan 方法，计算从当前方格横向或纵向移动到达目标所经过的方格数，忽略对角移动，然后把总数乘以 10 。之所以叫做 Manhattan 方法，是因为这很像统计从一个地点到另一个地点所穿过的街区数，而你不能斜向穿过街区。重要的是，计算 H 是，要忽略路径中的障碍物。这是对剩余距离的估算值，而不是实际值，因此才称为试探法。

把 G 和 H 相加便得到 F 。我们第一步的结果如下图所示。每个方格都标上了 F ， G ， H 的值，就像起点右边的方格那样，左上角是 F ，左下角是 G ，右下角是 H 。

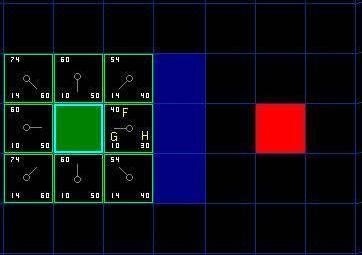
图 3

好，现在让我们看看其中的一些方格。在标有字母的方格， G = 10 。这是因为水平方向从起点到那里只有一个方格的距离。与起点直接相邻的上方，下方，左方的方格的 G 值都是 10 ，对角线的方格 G 值都是 14 。

H 值通过估算起点于终点 ( 红色方格 ) 的 Manhattan 距离得到，仅作横向和纵向移动，并且忽略沿途的墙壁。使用这种方式，起点右边的方格到终点有 3 个方格的距离，因此 H = 30 。这个方格上方的方格到终点有 4 个方格的距离 ( 注意只计算横向和纵向距离 ) ，因此 H = 40 。对于其他的方格，你可以用同样的方法知道 H 值是如何得来的。

每个方格的 F 值，再说一次，直接把 G 值和 H 值相加就可以了。

继续搜索(Continuing the Search)

为了继续搜索，我们从 open list 中选择 F 值最小的 ( 方格 ) 节点，然后对所选择的方格作如下操作：

4.       把它从 open list 里取出，放到 close list 中。

5.       检查所有与它相邻的方格，忽略其中在 close list 中或是不可走 (unwalkable) 的方格 ( 比如墙，水，或是其他非法地形 ) ，如果方格不在open lsit 中，则把它们加入到 open list 中。

把我们选定的方格设置为这些新加入的方格的父亲。

6.       如果某个相邻的方格已经在 open list 中，则检查这条路径是否更优，也就是说经由当前方格 ( 我们选中的方格 ) 到达那个方格是否具有更小的 G 值。如果没有，不做任何操作。

相反，如果 G 值更小，则把那个方格的父亲设为当前方格 ( 我们选中的方格 ) ，然后重新计算那个方格的 F 值和 G 值。如果你还是很混淆，请参考下图。

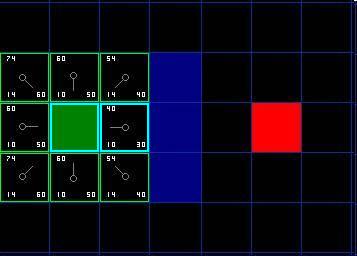
图 4

Ok ，让我们看看它是怎么工作的。在我们最初的 9 个方格中，还有 8 个在 open list 中，起点被放入了 close list 中。在这些方格中，起点右边的格子的 F 值 40 最小，因此我们选择这个方格作为下一个要处理的方格。它的外框用蓝线打亮。

首先，我们把它从 open list 移到 close list 中 ( 这就是为什么用蓝线打亮的原因了 ) 。然后我们检查与它相邻的方格。它右边的方格是墙壁，我们忽略。它左边的方格是起点，在 close list 中，我们也忽略。其他 4 个相邻的方格均在 open list 中，我们需要检查经由这个方格到达那里的路径是否更好，使用 G 值来判定。让我们看看上面的方格。它现在的 G 值为 14 。如果我们经由当前方格到达那里， G 值将会为 20(其中 10 为到达当前方格的 G 值，此外还要加上从当前方格纵向移动到上面方格的 G 值 10) 。显然 20 比 14 大，因此这不是最优的路径。如果你看图你就会明白。直接从起点沿对角线移动到那个方格比先横向移动再纵向移动要好。

当把 4 个已经在 open list 中的相邻方格都检查后，没有发现经由当前方格的更好路径，因此我们不做任何改变。现在我们已经检查了当前方格的所有相邻的方格，并也对他们作了处理，是时候选择下一个待处理的方格了。

因此再次遍历我们的 open list ，现在它只有 7 个方格了，我们需要选择 F 值最小的那个。有趣的是，这次有两个方格的 F 值都 54 ，选哪个呢？没什么关系。从速度上考虑，选择最后加入 open list 的方格更快。这导致了在寻路过程中，当靠近目标时，优先使用新找到的方格的偏好。但是这并不重要。 ( 对相同数据的不同对待，导致两中版本的 A* 找到等长的不同路径 ) 。

我们选择起点右下方的方格，如下图所示。

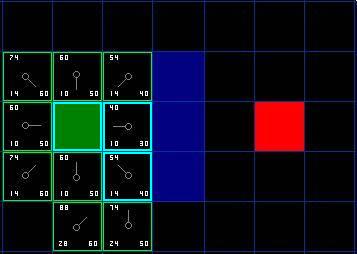
图 5

这次，当我们检查相邻的方格时，我们发现它右边的方格是墙，忽略之。上面的也一样。

我们把墙下面的一格也忽略掉。为什么？因为如果不穿越墙角的话，你不能直接从当前方格移动到那个方格。你需要先往下走，然后再移动到那个方格，这样来绕过墙角。 ( 注意：穿越墙角的规则是可选的，依赖于你的节点是怎么放置的 )

这样还剩下 5 个相邻的方格。当前方格下面的 2 个方格还没有加入 open list ，所以把它们加入，同时把当前方格设为他们的父亲。在剩下的3 个方格中，有 2 个已经在 close list 中 ( 一个是起点，一个是当前方格上面的方格，外框被加亮的 ) ，我们忽略它们。最后一个方格，也就是当前方格左边的方格，我们检查经由当前方格到达那里是否具有更小的 G 值。没有。因此我们准备从 open list 中选择下一个待处理的方格。

不断重复这个过程，直到把终点也加入到了 open list 中，此时如下图所示。

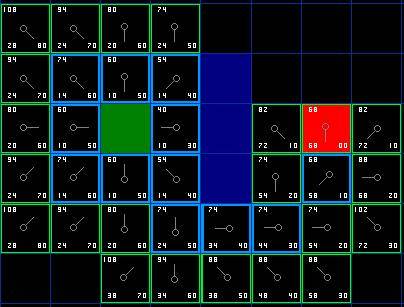
图 6

注意，在起点下面 2 格的方格的父亲已经与前面不同了。之前它的 G 值是 28 并且指向它右上方的方格。现在它的 G 值为 20 ，并且指向它正上方的方格。这在寻路过程中的某处发生，使用新路径时 G 值经过检查并且变得更低，因此父节点被重新设置， G 和 F 值被重新计算。尽管这一变化在本例中并不重要，但是在很多场合中，这种变化会导致寻路结果的巨大变化。

那么我们怎么样去确定实际路径呢？很简单，从终点开始，按着箭头向父节点移动，这样你就被带回到了起点，这就是你的路径。如下图所示。从起点 A 移动到终点 B 就是简单从路径上的一个方格的中心移动到另一个方格的中心，直至目标。就是这么简单！

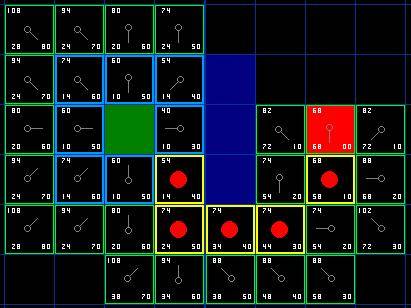
图 7

A*算法总结(Summary of the A* Method)

Ok ，现在你已经看完了整个的介绍，现在我们把所有步骤放在一起：

1.         把起点加入 open list 。

2.         重复如下过程：

a.         遍历 open list ，查找 F 值最小的节点，把它作为当前要处理的节点。

b.         把这个节点移到 close list 。

c.         对当前方格的 8 个相邻方格的每一个方格？

◆     如果它是不可抵达的或者它在 close list 中，忽略它。否则，做如下操作。

◆     如果它不在 open list 中，把它加入 open list ，并且把当前方格设置为它的父亲，记录该方格的 F ， G 和 H 值。

◆     如果它已经在 open list 中，检查这条路径 ( 即经由当前方格到达它那里 ) 是否更好，用 G 值作参考。更小的 G 值表示这是更好的路径。如果是这样，把它的父亲设置为当前方格，并重新计算它的 G 和 F 值。如果你的 open list 是按 F 值排序的话，改变后你可能需要重新排序。

d.         停止，当你

◆     把终点加入到了 open list 中，此时路径已经找到了，或者

◆     查找终点失败，并且 open list 是空的，此时没有路径。

3.         保存路径。从终点开始，每个方格沿着父节点移动直至起点，这就是你的路径。

上面原文：https://blog.csdn.net/weixin_44489823/article/details/89382502

=============================================================================================

下面是我自己实现的

在实现A*寻路过程中，我自己有几个点绕了好久

1.每一次找到下一个点后，搜索列表里面的点的G是按照起点还是当前点计算

我当前还是按照当前点来计算的，这个我还是有点疑问，需要自己想一想

2.搜索列表里面已有的点，在当前点改变时，如果为当前点的附近点时，他的父节点是否变为当前点

结果是不用的，这个应该是我刚开始没看太明白；只有当前点的下一级点为已有搜索点，并且当前点的索引<下一级点当前的父节点的索引时，才将下一级点的父节点改为当前点

==============================================================================================================================

暂时先这样，后面补充

（今天你加班吗 :> 我不加）