[zoj 3416/hdu 3709]数位DP

题意：求从区间[L, R]内有多少个数是平衡数，平衡数是指以10进制的某一位为中心轴，左右两边的每一位到中心轴的距离乘上数位上的值的和相等。0<=L<=R<=1e18

思路：由于任何非0正数最多只有1个位置作为中心轴使得它是平衡数。于是可以按中心轴的位置分类统计答案。令dp[p][i][j]表示中心轴在p位（p>=0)前i位且左边比右边的加权和已经多j的方案数，枚举当前第i位放的数k，那么dp[p][i][j]=∑dp[p][i-1][j+(p-i+1)*k]。

求出dp值后，只需从高位向低位统计，统计时也是按中心轴分类，即枚举中心轴，然后根据前多少位相同，维护一下已确定的数到中心轴的加权和，然后加上对应dp值。由于0这个数无论以什么作为中心轴都会使答案加1，所以最后需减去重复的。

 #pragma comment(linker, "/STACK:10240000,10240000")

 #include <iostream>
 #include <cstdio>
 #include <algorithm>
 #include <cstdlib>
 #include <cstring>
 #include <map>
 #include <queue>
 #include <deque>
 #include <cmath>
 #include <vector>
 #include <ctime>
 #include <cctype>
 #include <set>
 #include <bitset>
 #include <functional>
 #include <numeric>
 #include <stdexcept>
 #include <utility>

 using namespace std;

 #define mem0(a) memset(a, 0, sizeof(a))
 #define mem_1(a) memset(a, -1, sizeof(a))
 #define lson l, m, rt << 1
 #define rson m + 1, r, rt << 1 | 1
 #define rep_up0(a, b) for (int a = 0; a < (b); a++)
 #define rep_up1(a, b) for (int a = 1; a <= (b); a++)
 #define rep_down0(a, b) for (int a = b - 1; a >= 0; a--)
 #define rep_down1(a, b) for (int a = b; a > 0; a--)
 #define all(a) (a).begin(), (a).end()
 #define lowbit(x) ((x) & (-(x)))
 #define constructInt4(name, a, b, c, d) name(int a = 0, int b = 0, int c = 0, int d = 0): a(a), b(b), c(c), d(d) {}
 #define constructInt3(name, a, b, c) name(int a = 0, int b = 0, int c = 0): a(a), b(b), c(c) {}
 #define constructInt2(name, a, b) name(int a = 0, int b = 0): a(a), b(b) {}
 #define pchr(a) putchar(a)
 #define pstr(a) printf("%s", a)
 #define sstr(a) scanf("%s", a)
 #define sint(a) scanf("%d", &a)
 #define sint2(a, b) scanf("%d%d", &a, &b)
 #define sint3(a, b, c) scanf("%d%d%d", &a, &b, &c)
 #define pint(a) printf("%d\n", a)
 #define test_print1(a) cout << "var1 = " << a << endl
 #define test_print2(a, b) cout << "var1 = " << a << ", var2 = " << b << endl
 #define test_print3(a, b, c) cout << "var1 = " << a << ", var2 = " << b << ", var3 = " << c << endl
 #define mp(a, b) make_pair(a, b)
 #define pb(a) push_back(a)

 typedef unsigned int uint;
 typedef long long LL;
 typedef pair<int, int> pii;
 typedef vector<int> vi;

 const int dx[] = {, , -, , , , -, -};
 const int dy[] = {-, , , , , -, , - };
 const int maxn = 1e5 + ;
 const int md = ;
 const int inf = 1e9 + ;
 const LL inf_L = (LL)1e18 + ;
 const double pi = acos(-1.0);
 const double eps = 1e-;

 template<class T>T gcd(T a, T b){return b==?a:gcd(b,a%b);}
 template<class T>bool max_update(T &a,const T &b){if(b>a){a = b; return true;}return false;}
 template<class T>bool min_update(T &a,const T &b){if(b<a){a = b; return true;}return false;}
 template<class T>T condition(bool f, T a, T b){return f?a:b;}
 template<class T>void copy_arr(T a[], T b[], int n){rep_up0(i,n)a[i]=b[i];}
 int make_id(int x, int y, int n) { return x * n + y; }

 struct Node {
     LL a[];
     LL &operator [] (const int x) {
         return a[x + ];
     }
 } dp[][];

 void div_digit(LL x, int a[], int &n) {
     int p = ;
     a[p ++] = x % ;
     x /= ;
     while (x) {
         a[p ++] = x % ;
         x /= ;
     }
     n = p;
 }

 void init() {
     rep_up0(p, ) dp[p][][] = ;
     rep_up0(p, ) {
         rep_up1(i, ) {
             for (int j = -; j <= ; j ++) {
                 rep_up0(k, ) {
                     int val = j + (p - i + ) * k;
                     if (val < - || val > ) continue;
                     dp[p][i][j] += dp[p][i - ][val];
                 }
             }
         }
     }
 }

 LL calc(LL n) {
     if (n == -) return ;
     if (n == (LL)1e18) return (LL);
     LL ans = ;
     int a[], len;
     div_digit(n, a, len);
     rep_up0(p, ) {
         int sum = ;
         rep_down0(i, len) {
             rep_up0(j, a[i]) {
                 int val = sum + (p - i) * j;
                 if (val < - || val > ) continue;
                 ans += dp[p][i][val];
             }
             sum += a[i] * (p - i);
         }
     }
     rep_up0(p, ) {
         int sum = ;
         rep_down0(i, len) {
             sum += a[i] * (p - i);
         }
         if (sum == ) ans ++;
     }
     return ans - ;
 }

 int main() {
     //freopen("in.txt", "r", stdin);
     init();
     int T;
     cin >> T;
     LL n, m;
     while (T --) {
         cin >> n >> m;
         cout << calc(m) - calc(n - ) << endl;
     }
     return ;
 }

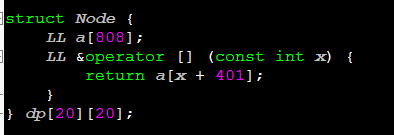
另外，灵机一动想出来一种写法（如有雷同，纯属巧合），用起来也还不错哦！