第二章 置信区间估计

估计量和估计值的写法？

估计值希腊字母上边有一个hat

点估计中矩估计的原理？

用样本矩来估计总体矩,用样本矩的连续函数来估计总体矩的连续函数,这种估计法称为矩估计法。Eg：如果一阶矩则样本均值估计总体均值

公式化之后的表达：

其中的μ1的表达式：

矩估计和最大似然估计最终估计的特点是什么？

二项分布的均值两种估计都相同，正态分布的均值两种估计都相同。但是其他分布仍存在不同的现象。

无偏性是什么？

估计值的均值与总体均值相同，除中间值之外的部分是随机误差。

均值的无偏性特殊在哪里？

任何存在期望的分布估计均值都是无偏的。

什么是无偏化？

就是利用数学变换得到无偏表达

一个参数可以有不同的无偏估计量吗？

可以。

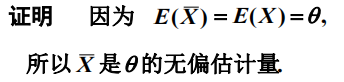
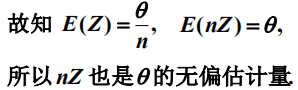
有效性的主体的是什么？

估计量的方差越小越有效。Eg：估计的总体均值的方差较小则比较有效。

区间估计和点估计谁是具有随机性的？

区间估计。因为点估计是估计一个原始数值，而区间估计是一个原始分布。

置信区间的定义举例解释？

想要估计总体均值，做100次实验，每次实验抽20个样本。处理后得到100个抽样分布区间，有95个区间中存在总体参数，就说有95%的把握认为你只使用一次实验数据的20个样本得到的置信区间中含有总体均值。

枢轴量是什么？

就是参数估计中的待估参数。

求置信区间的三步？

1.样本数据的总体分布2.置信度3.代公式计算

似然函数形式上是什么？

在已知样本来自于何分布之后，虽然不知道该分布中的参数是何值，但是可以反求出，所以一开始用某些字母代替，这样每一个样本x值通过分布率/概率密度对应一个该点概率值，将这些概率值的乘积连乘的结果就是似然函数。

点估计方法的使用顺序？

在统计问题中往往先使用最大似然估计法, 在最大似然估计法使用不方便时, 再用矩估计法。

伯努利大数定理是什么？

当样本量足够大的时候频率趋近于概率。

什么是用t分布的信号?

总体方差未知时

现阶段学习的估计条件是什么？

总体来自正态分布：

哪些问题要考虑单侧置信区间？

在某些实际问题中, 例如, 对于设备、元件的寿命来说, 平均寿命长是我们希望的, 我们关心的是平均寿命 的“下限”; 与之相反, 在考虑产品的废品率 p时, 我们常关心参数 p的 “上限” , 这就引出了单侧置信区间的概念。

对称分布和非对称分布的区别在抽样函数上有何区别？

对称函数的两边界取值是正负相反数即可：

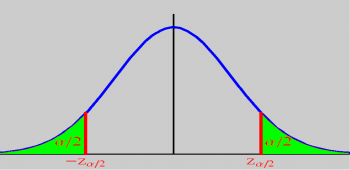
非对称函数的两边界取值要计算两边置信度相关数值：

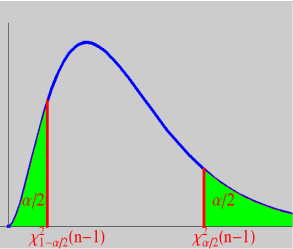
估计量|估计值|矩估计|最大似然估计|无偏性|无偏化|有效性|置信区间|枢轴量|似然函数|伯努利大数定理|t分布|单侧置信区间|抽样函数|的更多相关文章

  1. 详解最大似然估计（MLE）、最大后验概率估计（MAP），以及贝叶斯公式的理解

    转载声明:本文为转载文章,发表于nebulaf91的csdn博客.欢迎转载,但请务必保留本信息,注明文章出处. 原文作者: nebulaf91 原文原始地址:http://blog.csdn.net/ ...

  2. 抽样分布|t分布|中心极限定理|点估计|矩估计|最大似然法|

    生物统计与实验设计-统计学基础-2&区间估计-1 正态分布参数:均值和方差 其中,选择1d是因为好算:通常,95%区分大概率事件和小概率事件, 当总体是正态分布时,可以利用常用抽样分布估计出样 ...

  3. 【模式识别与机器学习】——最大似然估计 （MLE） 最大后验概率（MAP）和最小二乘法

    1) 极/最大似然估计 MLE 给定一堆数据,假如我们知道它是从某一种分布中随机取出来的,可是我们并不知道这个分布具体的参,即“模型已定,参数未知”.例如,我们知道这个分布是正态分布,但是不知道均值和 ...

  4. 最大似然估计 （MLE） 最大后验概率（MAP）

    1) 最大似然估计 MLE 给定一堆数据,假如我们知道它是从某一种分布中随机取出来的,可是我们并不知道这个分布具体的参,即"模型已定,参数未知". 例如,我们知道这个分布是正态分布 ...

  5. 最大似然估计 （MLE）与 最大后验概率（MAP）在机器学习中的应用

    最大似然估计 MLE 给定一堆数据,假如我们知道它是从某一种分布中随机取出来的,可是我们并不知道这个分布具体的参,即“模型已定,参数未知”. 例如,对于线性回归,我们假定样本是服从正态分布,但是不知道 ...

  6. 最大似然估计(MLE)与最小二乘估计(LSE)的区别

    最大似然估计与最小二乘估计的区别 标签(空格分隔): 概率论与数理统计 最小二乘估计 对于最小二乘估计来说,最合理的参数估计量应该使得模型能最好地拟合样本数据,也就是估计值与观测值之差的平方和最小. ...

  7. 4.机器学习——统计学习三要素与最大似然估计、最大后验概率估计及L1、L2正则化

    1.前言 之前我一直对于“最大似然估计”犯迷糊,今天在看了陶轻松.忆臻.nebulaf91等人的博客以及李航老师的<统计学习方法>后,豁然开朗,于是在此记下一些心得体会. “最大似然估计” ...

  8. 【机器学习基本理论】详解最大似然估计（MLE）、最大后验概率估计（MAP），以及贝叶斯公式的理解

    [机器学习基本理论]详解最大似然估计(MLE).最大后验概率估计(MAP),以及贝叶斯公式的理解 https://mp.csdn.net/postedit/81664644 最大似然估计(Maximu ...

  9. 最大似然估计（Maximum Likelihood，ML）

    先不要想其他的,首先要在大脑里形成概念! 最大似然估计是什么意思?呵呵,完全不懂字面意思,似然是个啥啊?其实似然是likelihood的文言翻译,就是可能性的意思,所以Maximum Likeliho ...

随机推荐

  1. php srand()和rand()

    1.rand()函数 作用:返回随机整数 用法:rand(min,max)  min和max规定随机数产生的范围,可以省略不写,不写时rand() 返回 0 到 RAND_MAX 之间的伪随机整数. ...

  2. java基础源码 (5)--reflect包-AccessibleObject类

    学习参考博客:https://blog.csdn.net/benjaminzhang666/article/details/9664585AccessibleObject类基本作用 1.将反射的对象标 ...

  3. OpenCV3 Ref SVM ： cv::ml::SVM Class Reference

    OpenCV3  Ref SVM : cv::ml::SVM Class Reference OpenCV2: #include <opencv2/core/core.hpp>#inclu ...

  4. IE8兼容问题汇总

    一.css的hack写法 IE8 CSS hack 就是在属性后面加上 \9 或者 \0,代码如下: color:#FFF\0; /* IE8 */ color:#FFF\9; /* 所有IE浏览器( ...

  5. 实验吧web-易-拐弯抹角(url伪静态)

    <?php // code by SEC@USTC echo '<html><head><meta http-equiv="charset" c ...

  6. expdp远程导出oracle库

    1.手动在本地建目录 E:\lvchengData 2.执行命令 create or replace directory data as 'E:\lvchengData\'; 3.为本地system用 ...

  7. English Words and Expressions

    Words apprentice 学徒 corny 老套的 obnoxious 作呕的 intermezzo 间奏曲 predate 日期上早于 parenthesis 括号 delimiter 分隔 ...

  8. [DDCTF 2019]homebrew event loop

    0x00 知识点 逻辑漏洞: 异步处理导致可以先调用增加钻石,再调用计算价钱的.也就是先货后款. eval函数存在注入,可以通过#注释,我们可以传入路由action:eval#;arg1#arg2#a ...

  9. JAVA函数库

    1. 文件相关 1.1 判断目录是否存在 public static boolean dictionaryExist(String path) { File file = new File(path) ...

  10. POJ 1844：Sum ”滚动“数组

    Sum Time Limit: 1000MS   Memory Limit: 30000K Total Submissions: 10494   Accepted: 6895 Description ...