FWT,FST入门

0.目录

目录

• 0.目录
• 1.什么是 FWT
• 2. FWT 怎么做
  • 2.1. 或卷积
  • 2.2.与卷积
  • 2.3.异或卷积
  • 2.4.例题
• 3. FST
  • 3.1. FST 怎么做
  • 3.2.例题

1.什么是 FWT

   FWT 全称为 " 快速沃尔什变换： Fast Walsh Transform " 。可以用于解决位运算卷积的问题。

  什么叫位运算卷积呢？我们考虑普通的卷积，即：

\[C_k=\sum_{i+j=k}A_iB_j
\]

  位运算卷积就是下标为位运算的卷积（此处与和或用 C++ 记号，异或用\(\oplus\)）：

\[\begin{aligned}\text{与卷积：}&C_k=\sum_{i\&j=k}A_iB_j\\\text{或卷积：}&C_k=\sum_{i|j=k}A_iB_j\\\text{异或卷积：}&C_k=\sum_{i\oplus j=k}A_iB_j\end{aligned}
\]

2. FWT 怎么做

  为了方便，以下我们假设所有向量长度都相等，为\(2\)的整幂，即长度\(n=2^m\)。高位以 0 补齐。

  设一个向量\(A\)经过 FWT 之后得到了\(FWT(A)\)， FWT 的最终目标就是满足：\(FWT(C)=FWT(A)\cdot FWT(B)\)，其中的点乘表示向量的每一位相乘：\(A\cdot B=(A_0B_0,A_1B_1,...,A_iB_i,...)\)。

   FWT 针对三种位运算有各自的处理方法：

2.1. 或卷积

  我们发现或运算存在如下的性质：

\[(j|i=i)\land (k|i=i)\Rightarrow (j|k)|i=i
\]

  如果将二进制理解为一个 01 集合，我们就可以用集合并的方式理解上面的性质。发现这其实是一个伪分配律。

  根据这个性质我们可以进行构造：

\[a_i=\sum_{j|i=i}A_j\\b_i=\sum_{j|i=i}B_j\\c_i=\sum_{j|i=i}C_j
\]

  那么可以发现：

\[\begin{aligned}
a_ib_i
&=\sum_{j|i=i}A_j\times \sum_{k|i=i}B_k\\
&=\sum_{j|i=i}\sum_{k|i=i}A_jB_k\\
&=\sum_{(j|k)|i=i}A_jB_k\\
&=c_i
\end{aligned}
\]

  这样做了对应乘法之后就可以得到\(c\)，再进行一次逆变换就可以得到\(C\)。

  因此问题变成了怎么进行这样的变换。

  考虑一种分治（或者称为 DP ）的做法：

  \(f(i,j)\)：满足仅有低\(i\)位可能与\(j\)不同的，且与\(j\)或后得到\(j\)的下标所对应的数的和。

  或者可以被描述为：

\[f(i,j)=\sum_{\lfloor\frac k{2^i}\rfloor=\lfloor\frac j{2^i}\rfloor,k|j=j} a_k
\]

  考虑如何进行转移，即从\(f(i-1)\)转移到\(f(i)\)。这种情况下只有第\(i\)位解除了限制。根据或的性质，如果第\(i\)位为 0 ，那么第\(i\)位或操作之后仍需要是 0 ，就只能从第\(i\)位为 0 的\(f(i,j)\)转移来；如果第\(i\)位为 1 ，那么第\(i\)位或操作总得到是 1 ，就可以不考虑第\(i\)位，从\(f(i,j)\)和\(f(i,j+2^i)\)转移来。

  放个图片理解一下：



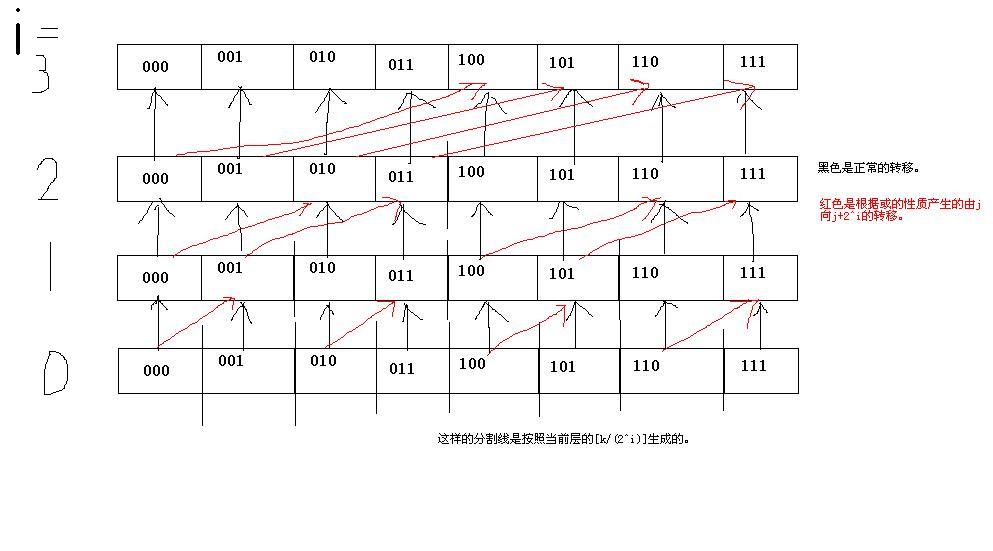
  顺便可以得到转移为：

  正变换：

\[\begin{aligned}
f(i,j)&=f(i-1,j)\\
f(i,j+2^i)&=f(i-1,j)+f(i-1,j+2^i)
\end{aligned}
\]

  逆变换就是将特殊贡献扣除：

\[\begin{aligned}
f(i,j)&=f(i+1,j)\\
f(i,j+2^i)&=f(i+1,j+2^i)-f(i+1,j)
\end{aligned}
\]

  可以发现\(f(0,i)=A_i\)，且这个转移可以滚动数组优化。

  这样的 FWT 就是\(O(n\log_2n)\)。

2.2.与卷积

  与卷积与或卷积十分相似，因此可以用类似的方法分析。这里只给出状态和转移：

\[f(i,j)=\sum_{\lfloor\frac k{2^i}\rfloor=\lfloor\frac j{2^i}\rfloor,k\&j=j} a_k
\]

  正变换：

\[\begin{aligned}
f(i,j)&=f(i-1,j)+f(i-1,j+2^i)\\
f(i,j+2^i)&=f(i-1,j+2^i)
\end{aligned}
\]

  逆变换：

\[\begin{aligned}
f(i,j)&=f(i+1,j)-f(i+1,j+2^i)\\
f(i,j+2^i)&=f(i+1,j+2^i)
\end{aligned}
\]

2.3.异或卷积

  我们同样考虑异或的性质。

  设\(count(i)\)为\(i\)的二进制中\(1\)的位数，\(i\otimes j=count(i\&j)\bmod 2\)则异或有性质：

\[(i\otimes j)\oplus(i\otimes k)=i\otimes (j\oplus k)
\]

  即奇偶性相等。设\(count(j\&i)=a,count(k\&i)=b,count(j\&k\&i)=c\)，则左侧奇偶性由\(a+b\)决定，右侧奇偶性由\(a+b-2c\)决定，可以发现两侧的奇偶性相等。

  说起奇偶性，我们可以想到\(-1\)的幂。于是设：

\[\begin{aligned}
a_i=\sum_j(-1)^{i\otimes j}A_j\\
b_i=\sum_j(-1)^{i\otimes j}B_j\\
c_i=\sum_j(-1)^{i\otimes j}C_j
\end{aligned}
\]

  然后就可以看看这样转换后乘起来的结果：

\[\begin{aligned}
a_ib_i
&=\sum_j(-1)^{i\otimes j}A_j\times \sum_k(-1)^{i\otimes k}B_k\\
&=\sum_{i\otimes j=0}\sum_{i\otimes k=0}A_jB_k-\sum_{i\otimes j=1}\sum_{i\otimes k=0}A_jB_k-\sum_{i\otimes j=0}\sum_{i\otimes k=1}A_jB_k+\sum_{i\otimes j=1}\sum_{i\otimes k=1}A_jB_k\\
&=\sum_{i\otimes (j\oplus k)=0}A_jB_k-\sum_{i\otimes (j\oplus k)=1}A_jB_k\\
&=\sum_p(-1)^{i\otimes p}\sum_{j\oplus k=p}A_jB_k\\
&=\sum_p(-1)^{i\otimes p}C_p\\
&=c_i
\end{aligned}
\]

  我们达成了目的。接下来就看看怎么变换。继续考虑 DP ：

\[f(i,j)=\sum_{\lfloor\frac k {2^i}\rfloor=\lfloor \frac j {2^i}\rfloor}(-1)^{j\otimes k}a_k
\]

  可以发现，从\(f(i-1)\)转到\(f(i)\)的时候，只有第\(i\)位都是\(1\)才会令\(j\otimes k\)改变奇偶性，即多乘上一个 -1 。

  这样转移，最终\(j\otimes k=0\)的情况就会被乘上偶数次 -1 ，而\(j\otimes k=1\)的情况就会被乘上奇数次 -1 ，最终答案就是正确的。

  按照这样，正变换：

\[\begin{aligned}
f(i,j)&=f(i-1,j)+f(i-1,j+2^i)\\
f(i,j+2^i)&=f(i-1,j)-f(i-1,j+2^i)
\end{aligned}
\]

  逆变换，用到了小学奥数的 " 和差问题 " 的结论：

\[\begin{aligned}
f(i,j)&=\frac{f(i+1,j)+f(i+1,j+2^i)} 2\\
f(i,j+2^i)&=\frac{f(i+1,j)-f(i+1,j+2^i)} 2
\end{aligned}
\]

  需要注意的是，异或卷积的逆变换还有一个 " 类 FFT " 的写法，即逆变换只比正变换在最后多除一个\(n\)（事实上异或 FWT 和 FFT 有很多相似处，可以在 K 进制 FWT 中找到答案）。

2.4.例题

  洛谷P4717。三种 FWT 全家桶。

  参考代码：

const int mod = 998244353, inv2 = 499122177;
const int MAXSIZ = 5e5 + 5;
int A[MAXSIZ], B[MAXSIZ], C[MAXSIZ], a[MAXSIZ], b[MAXSIZ];
int N, M;
int fix( const int x ) { return ( x % mod + mod ) % mod; }
namespace OR
{
	void FWT( int *f, const int m )
	{
		for( int s = 2 ; s <= M ; s <<= 1 )
			for( int i = 0, t = s >> 1 ; i < M ; i += s )
				for( int j = i ; j < i + t ; j ++ )
					f[j + t] = fix( f[j + t] + f[j] * m ) % mod;
	}
}
namespace AND
{
	void FWT( int *f, const int m )
	{
		for( int s = 2 ; s <= M ; s <<= 1 )
			for( int i = 0, t = s >> 1 ; i < M ; i += s )
				for( int j = i ; j < i + t ; j ++ )
					f[j] = fix( f[j] + f[j + t] * m ) % mod;
	}
}
namespace XOR
{
	void FWT( int *f, const int m )
	{
		int t1, t2;
		for( int s = 2 ; s <= M ; s <<= 1 )
			for( int i = 0, t = s >> 1 ; i < M ; i += s )
				for( int j = i ; j < i + t ; j ++ )
				{
					t1 = f[j], t2 = f[j + t];
					if( m > 0 )
						f[j] = ( t1 + t2 ) % mod,
						f[j + t] = fix( t1 - t2 );
					else
						f[j] = 1ll * ( t1 + t2 ) % mod * inv2 % mod,
						f[j + t] = 1ll * fix( t1 - t2 ) * inv2 % mod;
				}
	}
}
void cal( void ( *fwt ) ( int*, int ) )  //函数指针的写法，主要是方便。
{
	for( int i = 0 ; i < M ; i ++ ) A[i] = a[i], B[i] = b[i];
	fwt( A, 1 ), fwt( B, 1 );
	for( int i = 0 ; i < M ; i ++ ) C[i] = 1ll * A[i] * B[i] % mod;
	fwt( C, -1 );
	for( int i = 0 ; i < M ; i ++ ) write( C[i] ), putchar( i == M - 1 ? '\n' : ' ' );
}

3. FST

3.1. FST 怎么做

  它听着不妙。

  快速子集变换 FST 解决的是一类子集卷积的问题，即：

\[f(U)=\sum_{S,T\subseteq U, S\cup T=U, S\cap T=\varnothing} g(S)\times h(T)
\]

  这个卷积和或卷积的区别在于，或卷积可以有交集（并不要求\(j\& k=0\)），然而子集卷积不可以有。

  注意到这个限制在子集卷积中等价于\(|S|+|T|=|U|\)。因此我们可以给状态加上一维限制大小：

  \(f(i,U)\)：大小为\(i\)的集合\(U\)的所有子集的贡献，\(g\)和\(h\)同理转换。

  这个信息可以直接用 FWT 正变换得到。

  因此有转移：

\[f(i,U)=\sum_j^i\sum_{S\cup T=U}g(i,S)\times h(i-j,T)
\]

  转移完成后需要 FWT 逆变换回来，再将不符合要求（集合大小不匹配）的清除。

3.2.例题

  [CF914G]Sum The Fibonacci， FWT + FST ，附赠题解一篇。