NOIP提高组2016 D1T2 【天天爱跑步】

码了一个下午加一个晚上吧。。。。。。

题目描述：

小c同学认为跑步非常有趣,于是决定制作一款叫做《天天爱跑步》的游戏。《天天爱跑步》是一个养成类游戏,需要玩家每天按时上线,完成打卡任务。

这个游戏的地图可以看作一一棵包含 n个结点和 n-1条边的树, 每条边连接两个结点,且任意两个结点存在一条路径互相可达。树上结点编号为从1到n的连续正整数。

现在有m个玩家,第i个玩家的起点为 Si,终点为 Ti 。每天打卡任务开始时,所有玩家在第0秒同时从自己的起点出发, 以每秒跑一条边的速度, 不间断地沿着最短路径向着自己的终点跑去, 跑到终点后该玩家就算完成了打卡任务。 (由于地图是一棵树, 所以每个人的路径是唯一的)

小c想知道游戏的活跃度, 所以在每个结点上都放置了一个观察员。 在结点jj的观察员会选择在第Wj秒观察玩家, 一个玩家能被这个观察员观察到当且仅当该玩家在第Wj秒也理到达了结点j。 小c想知道每个观察员会观察到多少人?

注意: 我们认为一个玩家到达自己的终点后该玩家就会结束游戏, 他不能等待一 段时间后再被观察员观察到。 即对于把结点j作为终点的玩家: 若他在第Wj秒前到达终点,则在结点j的观察员不能观察到该玩家;若他正好在第Wj秒到达终点,则在结点j的观察员可以观察到这个玩家。

数据范围：

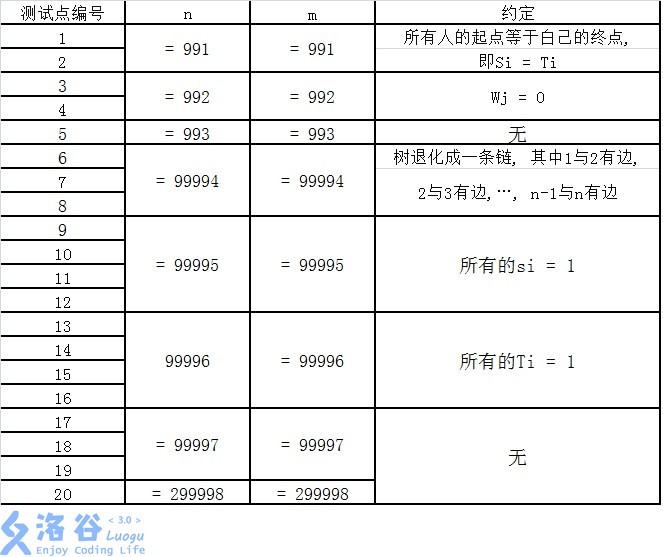
思路分析：

某王 云：任何题目的正解都是由部分分推导出来的，部分分就是在引导你走向正解。

嗯，好，我们开始讲部分分。

25分：

和人一起跳就是，lca O(n)就行，都不带优化的。

20分(s[i]=1)：

以根为起点，那么对于点u，显然只有当depth[u]=w[u]时，才有可能有路径能够对它产生贡献。

怎么样的路径才会对它产生贡献呢？——简单啊，t在以u为根的子树中就行了嘛。

那么这个值只要用树形DP搞一搞就行了。

20分(t[i]=1)：

以根为终点，对于节点u，只有起点在以u为根的子树中且深度为depth[u]+w[u]的路径才会对点u产生贡献。

我们可以搞一个桶，把起点深度相同的点全部丢进同一个桶bac[depth[s]]。

那么当我们访问到节点u时，一个变量pre记录一下当前bac[depth[u]+w[u]]的值，同时bac[depth[u]]+=tot[u]，其中tot[u]表示以u节点为起点的路径数量。

当我们要退出这个点时，ans[u]+=bac[depth[u]+w[u]]-pre。（“类似”差分）

吐槽一下：我刚做这题的时候，同学告诉我这题是差分，误导了我好久。。。。。。

100分（出现辣——正解！！！）：

嗯，某王 其实说的很对，特别有道理！——没错，正解就是“综上所述”

把一条链分为两段，s到lca一段（这段是往上走的），lca到t一段（这段是往下的）。

先分类讨论一下：

对于一个节点u，我们将对其产生贡献的路径分为两种：1：自下而上经过它，从而产生贡献。2：自上而下经过它，从而产生贡献。

1、自下而上：

这个和t[i]=1其实类似。

能用这种方式对点u产生贡献的路径需要满足：

1、起点在以u为根的子树中，终点在u以及u的祖先中。

2、depth[s]=depth[u]+w[u]

然后像t[i]=1那样用桶，类差分一下就行了。

更新操作：

bac[depth[u]]+=tot[u]

细节处理：

当我们要退出一个节点u时要枚举所有以u节点为lca的路径，然后bac[depth[s]]--。

为什么呢？——因为条件1嘛！

当u节点退出后，就会进入u的父亲，而这条路径的上半段对于u的父亲与u的兄弟是没有贡献的（因为这段路径的起点(lca)并不在它们自己或是它们的祖先中了）。

2、自上而下：

这个稍微难一点点。

能对节点u产生贡献的路径，起点不一定是u节点的祖先，也有可能是u的兄弟（这个能想象吧，就是先往上走，再折下来的那种）。

但是能对节点u产生贡献的路径，他们的起点与u的距离肯定是w[u]。

所以需要满足：

1、终点在以u为根的子树中，起点不在以u为根的子树中。

2、 depth[s]+depth[u]-2*depth[lca(s,u)]=w[u]

depth[s]-2*depth[lca(s,t)]+depth[u]=w[u]

depth[s]+depth[t]-2*depth[lca(s,t)]+depth[u]-depth[t]=w[u]

len[s,t]-depth[t]=w[u]-depth[u]

这里讲一下为什么lca(s,u)=lca(s,t)吧，因为不管这条路径属于上面两种情况的哪一种，只要满足了条件1，那么depth[lca(s,t)]>=depth[u]对吧，而t又在以u为根的子树中，那么lca肯定不会变啊。

同样的，用桶类差分即可。

但是此时类差分的时候要注意：把s丢进bac[len[s,t]-depth[t]]中，询问时要找的桶是bac[w[u]-depth[u]]（上面应该讲的很清楚了吧）。

更新操作：

退出一个节点时，枚举所有以u为终点的路径，然后bac[depth[len[s,t]-depth[t]]]++。

细节处理：

退出一个节点时，枚举所有以u为lca的路径，然后bac[depth[len[s,t]-depth[t]]]--。（这个和上面差不多就不讲了）

代码实现：

var
  head:array[1..4,0..300000]of longint;
  next,len,vet:array[1..2000000]of longint;
  vis:array[0..300000]of boolean;
  depth,ans,sum,w:array[0..300000]of longint;
  bac:array[-300000..300000]of longint;
  f:array[0..300000,0..20]of longint;
  i,n,m,x,y,s,t,z,tot,l:longint;
procedure add(k,x,y,z:longint);
begin
  inc(tot);
  next[tot]:=head[k,x];
  vet[tot]:=y;
  head[k,x]:=tot;
  len[tot]:=z;
end;
procedure dfs(u,dep:longint);
var
  i,v:longint;
begin
  depth[u]:=dep; vis[u]:=true;
  for i:=1 to 20 do
    f[u,i]:=f[f[u,i-1],i-1];
  i:=head[1,u];
  while i<>0 do
  begin
    v:=vet[i];
    if not vis[v] then
      begin f[v,0]:=u; dfs(v,dep+1); end;
    i:=next[i];
  end;
end;
function lca(a,b:longint):longint;
var
  i,t:longint;
begin
  if depth[a]>depth[b] then begin t:=a; a:=b; b:=t; end;
  for i:=20 downto 0 do
    if depth[f[b,i]]>=depth[a] then b:=f[b,i];
  if a=b then exit(a);
  for i:=20 downto 0 do
    if f[a,i]<>f[b,i] then
      begin a:=f[a,i]; b:=f[b,i]; end;
  exit(f[a,0]);
end;
procedure up(u,father:longint);
var
  i,v,s,pre:longint;
begin
  pre:=bac[w[u]+depth[u]];
  i:=head[1,u];
  while i<>0 do
  begin
    v:=vet[i];
    if v<>father then up(v,u);
    i:=next[i];
  end;
  bac[depth[u]]:=bac[depth[u]]+sum[u];
  ans[u]:=ans[u]+bac[w[u]+depth[u]]-pre;
  i:=head[2,u];
  while i<>0 do
    begin s:=vet[i]; dec(bac[depth[s]]); i:=next[i]; end;
end;
procedure down(u,father:longint);
var
  i,pre,s,t,v:longint;
begin
  pre:=bac[w[u]-depth[u]];
  i:=head[1,u];
  while i<>0 do
  begin
    v:=vet[i];
    if v<>father then down(v,u);
    i:=next[i];
  end;
  i:=head[4,u];
  while i<>0 do
    begin t:=vet[i]; inc(bac[len[i]-depth[t]]); i:=next[i]; end;
  ans[u]:=ans[u]+bac[w[u]-depth[u]]-pre;
  i:=head[3,u];
  while i<>0 do
    begin t:=vet[i]; dec(bac[len[i]-depth[t]]); i:=next[i]; end;
end;
begin
  read(n,m);
  for i:=1 to n-1 do
  begin
    read(x,y);
    add(1,x,y,0); add(1,y,x,0);
  end;
  dfs(1,1);
  for i:=1 to n do read(w[i]);
  for i:=1 to m do
  begin
    read(s,t); z:=lca(s,t); inc(sum[s]); l:=depth[s]+depth[t]-2*depth[z];
    if depth[s]-depth[z]=w[z] then dec(ans[z]);
    add(2,z,s,0); add(3,z,t,l); add(4,t,t,l);
  end;
  up(1,0);
  fillchar(bac,sizeof(bac),0);
  down(1,0);
  for i:=1 to n do
    write(ans[i],' ');
end.                                            //感觉guide不好用。。。。。。