【ZJOI2019】线段树（线段树 & dp）

Link

UOJ LOJ Luogu

Solution

很玄妙的一道题，考察了对线段树较本质的理解 然而我并不会这个所谓最可做的题

首先，虽然题目很复杂，好像每个点的标记变化都很玄学，但是我们可以深入挖一挖性质。

假设我们现在的总区间为 \([1, 16]\)，现在执行了修改 \(\text{M}\small\text{ODIFY}\)\([4, 10]\)，那么线段树上的结点状况如下：

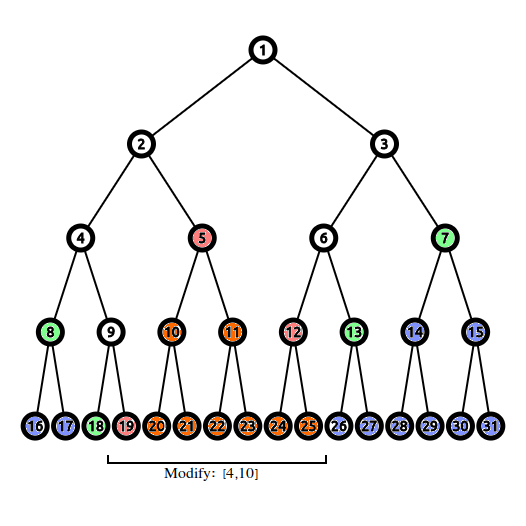
根据各个结点的性质我们将其分类。

• Type 1：未标记，与询问区间半覆盖，这些结点上的标记会全部被 \(\text P\small\text{USHDOWN}\)。
• Type 2：用红色标记，与询问区间全覆盖，恰好停止向下访问的结点，会在此处直接打标记走人。
• Type 3：用绿色标记，与询问区间无交，但可以得到来自 Type 1 \(\text P\small\text{USHDOWN}\) 而来的标记。
• Type 4：用橙色标记，与询问区间全覆盖，但无法被访问到。
• Type 5：用蓝色标记，与询问区间无交，同时也得不到 \(\text P\small\text{USHDOWN}\) 而来的标记。

注意到性质相同的结点可以相同处理，这便是我们分类的意义所在。

---

接下来考虑一个 dp。我们必然不能把线段树真的拿去复制，于是直接在一个线段树上搞。

很容易想到的一个状态是，\(f_i(x)\) 表示在第 \(i\) 次 \(\text{M}\small\text{ODIFY}\) 之后，所有线段树中，位置 \(x\) 上有 tag 的线段树有几棵。

但是这样是不够的：Type 3 的转移需要视其线段树上祖先的 tag 情况而定。

于是再设 \(g_i(x)\) 为第 \(i\) 次 \(\text{M}\small\text{ODIFY}\) 之后，所有线段树中，\(x\to 1\) （祖先）的路径上不存在任何一个 tag 的线段树有几棵。

这样一来 Type 3 的问题自然解决了。

根据结点的 Type 进行分类讨论，设计转移：

• Type 1：
  • 当前这个位置修改后必不可能存在标记，因为不管之前有没有都将被 \(\text P\small\text{USHDOWN}\)。
  • \(f_i(x) \leftarrow f_{i-1}(x)\)
  • \(g_i(x)\leftarrow g_{i-1}(x) + 2^{i-1}\)
• Type 2：
  • 当前这个位置修改后必定存在标记，因为我们打 tag 打的就是这。
  • \(f_i(x)\leftarrow f_{i-1}(x) + 2^{i-1}\)
  • \(g_i(x)\leftarrow g_{i-1}(x)\)
• Type 3：
  • 这里到底会不会有标记，还得看上头有没有东西可以传下来。
  • 其中共有 \(2^{i-1}-g_{i-1}(x)\) 棵线段树是存在至少一个标记的，只要有一个此处就得的到标记，这些会参与 \(f\) 的转移当中。
  • 至于 \(g\) 如何，原先有的还是有，没有的还是没有，该咋样咋样，复制一次刚好就 \(\times 2\)。
  • \(f_i(x)\leftarrow f_{i-1}(x)+2^{i-1}-g_{i-1}(x)\)
  • \(g_i(x)\leftarrow 2g_{i-1}(x)\)
• Type 4：
  • 由于 Type 4 的点在 Type 2 的点之下，而 Type 2 必定有 tag，于是上头不可能没有 tag。
  • 这里不会被遍历到，标记状况不会变，该咋样咋样。
  • \(f_i(x)\leftarrow 2f_{i-1}(x)\)
  • \(g_i(x)\leftarrow g_{i-1}(x)\)
• Type 5：
  • 被遗忘的角落，啥都不会变。
  • \(f_i(x)\leftarrow 2f_{i-1}(x)\)
  • \(g_i(x)\leftarrow 2g_{i-1}(x)\)

于是这题就做完了……吗？

我们发现，Type 1、2、3 的点数都不超过 \(O(\log n)\)，这些暴力的话问题也不大，不过 Type 4、5 的点数可以达到难以接受的 \(O(n)\)。

但别忘了，现在我们是在线段树上搞 dp！线段树的标配是什么？懒标记！

既然题面上都这么多标记，那我们 Type 4、5 同样可以打标记，而且只需要维护一个乘法标记就行了。

然后差不多真的就做完了，细节还是挺多的。注意这里空间需要开大一倍，我们比一般线段树多往下更新了一层。

实现的话，只要在伪代码基础上改改就行。

Code

/*
 * Author : _Wallace_
 * Source : https://www.cnblogs.com/-Wallace-/
 * Problem : ZJOI2019 线段树
 */
#include <cstdio>

using namespace std;
const int N = 1e5 + 5;
const int mod = 998244353;
typedef long long LL;

int n, m;
LL f[N << 3], g[N << 3];
LL tf[N << 3], tg[N << 3]; // multiplication tags
LL sf[N << 3]; // sum of f in a subtree

#define mid ((l + r) >> 1)
#define dirL x << 1, l, mid
#define dirR x << 1 | 1, mid + 1, r
void pushup(int x) {
  sf[x] = (sf[x << 1] + sf[x << 1 | 1] + f[x]) % mod;
}
void build(int x, int l, int r) {
  f[x] = 0ll, g[x] = 1ll, tf[x] = tg[x] = 1ll, sf[x] = 0ll;
  if (l == r) return;
  build(dirL), build(dirR), pushup(x);
}
void update_f(int x, LL v) {
  (f[x] *= v) %= mod, (sf[x] *= v) %= mod, (tf[x] *= v) %= mod;
}
void update_g(int x, LL v) {
  (g[x] *= v) %= mod, (tg[x] *= v) %= mod;
}
void pushdown(int x) {
  if (tf[x] != 1ll) {
    update_f(x << 1, tf[x]);
    update_f(x << 1 | 1, tf[x]);
    tf[x] = 1ll;
  }
  if (tg[x] != 1ll) {
    update_g(x << 1, tg[x]);
    update_g(x << 1 | 1, tg[x]);
    tg[x] = 1ll;
  }
}
LL k = 1ll;
void modify(int x, int l, int r, int ql, int qr) {
  pushdown(x);
  int lc = x << 1, rc = lc | 1;
  if (ql <= l && r <= qr) {
    (f[x] += k) %= mod; // type 2
    update_f(lc, 2), update_f(rc, 2); // type 4
  } else {
    (g[x] += k) %= mod; // type 1
    if (qr <= mid) {
      modify(dirL, ql, qr), pushdown(rc);
      (f[rc] += (k - g[rc] + mod) % mod) %= mod; // type 3
      (g[rc] *= 2) %= mod; // type 3
      update_f(rc << 1, 2), update_f(rc << 1 | 1, 2); // type 5
      update_g(rc << 1, 2), update_g(rc << 1 | 1, 2); // type 5
      pushup(rc);
    } else if (ql > mid) {
      modify(dirR, ql, qr), pushdown(lc);
      (f[lc] += (k - g[lc] + mod) % mod) %= mod; // type 3
      (g[lc] *= 2) %= mod; // type 3
      update_f(lc << 1, 2), update_f(lc << 1 | 1, 2); // type 5
      update_g(lc << 1, 2), update_g(lc << 1 | 1, 2); // type 5
      pushup(lc);
    } else {
      modify(dirL, ql, qr), modify(dirR, ql, qr);
    }
  }
  pushup(x);
}
#undef mid

signed main() {
  scanf("%d%d", &n, &m);
  build(1, 1, n);
  for (int i = 1; i <= m; i++) {
    int opt, l, r;
    scanf("%d", &opt);
    if (opt == 1) {
      scanf("%d%d", &l, &r);
      modify(1, 1, n, l, r);
      (k *= 2) %= mod;
    }
    else printf("%d\n", sf[1]);
  }
  return 0;
}