D. Mike and distribution 首先学习了一个玄学的东西

http://codeforces.com/contest/798/problem/D

D. Mike and distribution

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Mike has always been thinking about the harshness of social inequality. He's so obsessed with it that sometimes it even affects him while solving problems. At the moment, Mike has two sequences of positive integersA = [a1, a2, ..., an] and B = [b1, b2, ..., bn] of length n each which he uses to ask people some quite peculiar questions.

To test you on how good are you at spotting inequality in life, he wants you to find an "unfair" subset of the original sequence. To be more precise, he wants you to select k numbers P = [p1, p2, ..., pk] such that 1 ≤ pi ≤ n for1 ≤ i ≤ k and elements in P are distinct. Sequence P will represent indices of elements that you'll select from both sequences. He calls such a subset P "unfair" if and only if the following conditions are satisfied: 2·(ap1 + ... + apk)is greater than the sum of all elements from sequence A, and 2·(bp1 + ... + bpk) is greater than the sum of all elements from the sequence B. Also, k should be smaller or equal to 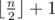 because it will be to easy to find sequence P if he allowed you to select too many elements!

Mike guarantees you that a solution will always exist given the conditions described above, so please help him satisfy his curiosity!

Input

The first line contains integer n (1 ≤ n ≤ 105) — the number of elements in the sequences.

On the second line there are n space-separated integers a1, ..., an (1 ≤ ai ≤ 109) — elements of sequence A.

On the third line there are also n space-separated integers b1, ..., bn (1 ≤ bi ≤ 109) — elements of sequence B.

Output

On the first line output an integer k which represents the size of the found subset. k should be less or equal to .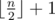

On the next line print k integers p1, p2, ..., pk (1 ≤ pi ≤ n) — the elements of sequence P. You can print the numbers in any order you want. Elements in sequence P should be distinct.

Example

input

5
8 7 4 8 3
4 2 5 3 7

output

3
1 4 5

用了一个叫random_shuffle的东西，每次都乱选，然后暴力前k个。

#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <assert.h>
#define IOS ios::sync_with_stdio(false)
using namespace std;
#define inf (0x3f3f3f3f)
typedef long long int LL;

#include <iostream>
#include <sstream>
#include <vector>
#include <set>
#include <map>
#include <queue>
#include <string>
#include <bitset>
const int maxn = 1e5 + ;
int a[maxn], b[maxn];

bool in[maxn];
LL sumA, sumB;
LL allA, allB;
int c[maxn];
int n, en;
bool ok() {
    LL ta = , tb = ;
    for (int i = ; i <= en; ++i) {
        ta +=  * a[c[i]];
        tb +=  * b[c[i]];
        if (ta > allA && tb > allB) return true;
    }
    return false;
}
void work() {
    cin >> n;
    for (int i = ; i <= n; ++i) {
        scanf("%d", &a[i]);
        allA += a[i];
    }
    for (int i = ; i <= n; ++i) {
        scanf("%d", &b[i]);
        allB += b[i];
        c[i] = i;
    }
    en = (n) /  + ;
    while (!ok()) {
        random_shuffle(c + , c +  + n);
//        for (int i = 1; i <= n; ++i) {
//            cout << c[i] << " ";
//        }
//        cout << endl;
    }
    cout << en<< endl;
    for (int i = ; i <= en; ++i) {
        printf("%d ", c[i]);
    }
}

int main() {
#ifdef LOCAL
    freopen("data.txt", "r", stdin);
//    freopen("data.txt", "w", stdout);
#endif
    work();
    return ;
}

正解：

首先注意到，选出n / 2 + 1个数，2倍的和大于总和，等价于选出n / 2 + 1个数，总和大于剩下的数。

因为可以取n / 2 + 1个，那么先对A排序，B不动，先把A[1]选了（这个是用在证明A数组成立用的），A【1】是当前A中最大的了。当然了也选了一个B，就是选了B[A[1].id]，

然后每两个做一pair，选一个比较大的B，也就是max(B[A[i].id], B[A[i + 1].id])

这样，B数组是满足的，这很容易证明，因为没一对中，都选了一个较大的。然后加上第一个，总和肯定大于剩下 的。

也就是

max(b[1], b[2]) >= min(b[1], b[2])

max(b[3], b[4]) >= min(b[3], b[4])

max(b[5], b[6]) >= min(b[5], b[6])

那么全部相加，不等号方向不变。而且开头还有一个b[A[1].id]加了进来，所以是严格大于的。

再来看看A的证明。

第一是选了a[1]

然后选a[2]和a[3]的那个呢？不固定的，还要看B，但是不管，有以下不等式。

a[1] >= any(a[2], a[3])

any(a[2], a[3]) >= any(a[4], a[5])

any(a[4], a[5]) >= any(a[5], a[6])

也就是，你选了一个a[1]，然后a[2]和a[3]选那个是没关系的，可以用a[1]和它比较，然后又因为选了any(a[2], a[3])，那么你a[4]和a[5]选那个是没所谓的，因为可以用any(a[2], a[3])和它比较。

最后，any(a[n - 1], a[n]) > 0，所以是严格大于的。

#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <assert.h>
#define IOS ios::sync_with_stdio(false)
using namespace std;
#define inf (0x3f3f3f3f)
typedef long long int LL;

#include <iostream>
#include <sstream>
#include <vector>
#include <set>
#include <map>
#include <queue>
#include <string>
#include <bitset>
const int maxn = 1e5 + ;
struct Node {
    int a, id;
    bool operator < (const struct Node & rhs) const {
        return a > rhs.a;
    }
}a[maxn];
int b[maxn];
vector<int>ans;
void work() {
    int n;
    cin >> n;
    for (int i = ; i <= n; ++i) {
        cin >> a[i].a;
        a[i].id = i;
    }
    for (int i = ; i <= n; ++i) {
        cin >> b[i];
    }
    sort(a + , a +  + n);
    int sel = n /  + ;
    ans.push_back(a[].id);
    for (int i = ; i <= n; i += ) {
        int want = a[i].id;
        if (i +  <= n && b[want] < b[a[i + ].id]) {
            want = a[i + ].id;
        }
        ans.push_back(want);
    }
    cout << ans.size() << endl;
    for (int i = ; i < ans.size(); ++i) {
        cout << ans[i] << " ";
    }
}

int main() {
#ifdef local
    freopen("data.txt", "r", stdin);
//    freopen("data.txt", "w", stdout);
#endif
IOS;
    work();
    return ;
}

2017-4-23 22:22:03

要开始补sg函数（博弈）和构造题。先复习下字符串准备省赛。