CF-839B

B. Game of the Rows

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Daenerys Targaryen has an army consisting of k groups of soldiers, the i-th group contains ai soldiers. She wants to bring her army to the other side of the sea to get the Iron Throne. She has recently bought an airplane to carry her army through the sea. The airplane has nrows, each of them has 8 seats. We call two seats neighbor, if they are in the same row and in seats {1, 2}, {3, 4}, {4, 5}, {5, 6} or {7, 8}.

A row in the airplane

Daenerys Targaryen wants to place her army in the plane so that there are no two soldiers from different groups sitting on neighboring seats.

Your task is to determine if there is a possible arranging of her army in the airplane such that the condition above is satisfied.

Input

The first line contains two integers n and k (1 ≤ n ≤ 10000, 1 ≤ k ≤ 100) — the number of rows and the number of groups of soldiers, respectively.

The second line contains k integers a1, a2, a3, ..., ak (1 ≤ ai ≤ 10000), where ai denotes the number of soldiers in the i-th group.

It is guaranteed that a1 + a2 + ... + ak ≤ 8·n.

Output

If we can place the soldiers in the airplane print "YES" (without quotes). Otherwise print "NO" (without quotes).

You can choose the case (lower or upper) for each letter arbitrary.

Examples

input

2 2
5 8

output

YES

input

1 2
7 1

output

NO

input

1 2
4 4

output

YES

input

1 4
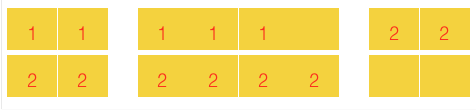
2 2 1 2

output

YES

Note

In the first sample, Daenerys can place the soldiers like in the figure below:

In the second sample, there is no way to place the soldiers in the plane since the second group soldier will always have a seat neighboring to someone from the first group.

In the third example Daenerys can place the first group on seats (1, 2, 7, 8), and the second group an all the remaining seats.

In the fourth example she can place the first two groups on seats (1, 2) and (7, 8), the third group on seats (3), and the fourth group on seats (5, 6).

题意：

有n排座位，有k组 每组有a[i]人，问能否使不同组的人都不相邻。

先将a[i]分为4 2 1，先放4的部分，再2，再1。

AC代码：

 #include<bits/stdc++.h>
 using namespace std;

 int a[];

 int main(){
     ios::sync_with_stdio(false);
     int n,k;
     cin>>n>>k;
     for(int i=;i<k;i++){
         cin>>a[i];
     }
     int sum1=n;
     int sum2=n*;
     for(int i=;i<k;i++){
         int d=min(sum1,a[i]/);
         sum1-=d;
         a[i]-=d*;
     }
     sum2+=sum1;
     for(int i=;i<k;i++){
         int d=min(sum2,a[i]/);
         sum2-=d;
         a[i]-=d*;
     }
     int temp=sum1+sum2;
     for(int i=;i<k;i++){
         temp-=a[i];
     }
     if(temp>=){
         cout<<"YES"<<endl;
     }
     else{
         cout<<"NO"<<endl;
     }
     return ;
 }