kmp和hash 字符串处理 哈希表

来自http://www.ruanyifeng.com/blog/2013/05/Knuth%E2%80%93Morris%E2%80%93Pratt_algorithm.html

并进行自己的简单整理，还加了代码实现。

因为作者实在太弱，以至自己找了一堆解释才弄明白，所以按照比较好懂的方式讲一讲

进入正题。

字符串匹配是计算机的基本任务之一。

举例来说，有一个字符串"BBC ABCDAB ABCDABCDABDE"（记为str1），我想知道，里面是否包含另一个字符串"ABCDABD"（记为str2）？

容易想到普通暴搜：

1.

首先，字符串"BBC ABCDAB ABCDABCDABDE"的第一个字符与搜索词"ABCDABD"的第一个字符，进行比较。因为B与A不匹配，所以搜索词后移一位。

2.

因为B与A不匹配，搜索词再往后移。

3.

就这样，直到字符串有一个字符，与搜索词的第一个字符相同为止。

4.

接着比较字符串和搜索词的下一个字符，还是相同。

5.

直到字符串有一个字符，与搜索词对应的字符不相同为止。

6.

这时，暴搜的反应是，将搜索词整个后移一位，再从头逐个比较。这样做虽然可行，但是效率很差，因为你要把"搜索位置"移到已经比较过的位置，重比一遍。

7.

一个基本事实是，当空格与D不匹配时，你其实知道前面六个字符是"ABCDAB"。KMP算法的想法是，设法利用这个已知信息，不要把"搜索位置"移回已经比较过的位置，继续把它向后移，这样就提高了效率。

在讲kmp之前，先引入一个概念--部分匹配值（数组next）。

首先，要了解两个概念："前缀"和"后缀"。 "前缀"指除了最后一个字符以外，一个字符串的全部头部组合；"后缀"指除了第一个字符以外，一个字符串的全部尾部组合。

1.

"部分匹配值"就是"前缀"和"后缀"的最长的共有元素的长度。以"ABCDABD"为例，

　　－　"A"的前缀和后缀都为空集，共有元素的长度为0；

　　－　"AB"的前缀为[A]，后缀为[B]，共有元素的长度为0；

　　－　"ABC"的前缀为[A, AB]，后缀为[BC, C]，共有元素的长度0；

　　－　"ABCD"的前缀为[A, AB, ABC]，后缀为[BCD, CD, D]，共有元素的长度为0；

　　－　"ABCDA"的前缀为[A, AB, ABC, ABCD]，后缀为[BCDA, CDA, DA, A]，共有元素为"A"，长度为1；

　　－　"ABCDAB"的前缀为[A, AB, ABC, ABCD, ABCDA]，后缀为[BCDAB, CDAB, DAB, AB, B]，共有元素为"AB"，长度为2；

　　－　"ABCDABD"的前缀为[A, AB, ABC, ABCD, ABCDA, ABCDAB]，后缀为[BCDABD, CDABD, DABD, ABD, BD, D]，共有元素的长度为0。

2.

"部分匹配"的实质是，有时候，字符串头部和尾部会有重复。比如，"ABCDAB"之中有两个"AB"，那么它的"部分匹配值"就是2（"AB"的长度）。搜索词移动的时候，第一个"AB"向后移动4位（字符串长度-部分匹配值），就可以来到第二个"AB"的位置。

现在来讲kmp

1.

这里是一张匹配表。

2.

已知空格与D不匹配时，前面六个字符"ABCDAB"是匹配的。查表可知，最后一个匹配字符B对应的"部分匹配值"为2，因此按照下面的公式算出向后移动的位数：

　　移动位数 = 已匹配的字符数 - 对应的部分匹配值

因为 6 - 2 等于4，所以将搜索词向后移动4位。

3.

因为空格与Ｃ不匹配，搜索词还要继续往后移。这时，已匹配的字符数为2（"AB"），对应的"部分匹配值"为0。所以，移动位数 = 2 - 0，结果为 2，于是将搜索词向后移2位。

4.

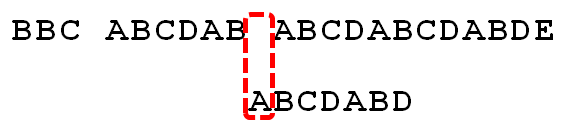
因为空格与A不匹配，继续后移一位。

5.

逐位比较，直到发现C与D不匹配。于是，移动位数 = 6 - 2，继续将搜索词向后移动4位。

6.

逐位比较，直到搜索词的最后一位，发现完全匹配，于是搜索完成。如果还要继续搜索（即找出全部匹配），移动位数 = 7 - 0，再将搜索词向后移动7位，这里就不再重复了。

最后是代码

我们来一部分一部分分开看

先是最重要的next（部分匹配值）

for(int i=;i<=len2;i++)//处理next
{
    while(i1&&str2[i1+]!=str2[i])
    //如果str2[i1+1]!=str2[i]那么这串连续的相等断了，所以我们无法继承之前的情况
    {
        i1=next[i1];
   //记得next的含义吗，顺着next我们可以找到能够让我们继续匹配的值，但i1不能为0并且如果我们找到了str2[i1+1]==str2[i]的地方，那么我们就可以从这里开始继承
    }
    if(str2[i1+]==str2[i])
    {
        i1++;//相等就比下一个，同时这也是计数+1
    }
    next[i]=i1;//把算出的值告诉next
}

其实我觉得kmp十分重要的一点就是理解求next和最后答案的联系

所谓next，其实就是自己（str2）和自己（str2）的一个部分匹配值

而最后答案与自己（str2）和别人（str1）的匹配有关

两者的实质是一样的，所以如果向下翻，看最后总代码的话，可以发现，两个for循环不过就是复制粘贴了一下，然后进行稍微改动（建议明白整个算法后，自行思考改动原因）

当你明白了这点，求str1和str2的匹配就不成问题了

所以我们就可以直接看总代码了

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
char str1[],str2[];
int len1,len2,i1;
int next[];
int main()
{
    scanf("%s %s",str1+,str2+);
    len1=strlen(str1+);
    len2=strlen(str2+);
    for(int i=;i<=len2;i++)//处理next
    {
        while(i1&&str2[i1+]!=str2[i])
        {
            i1=next[i1];
        }
        if(str2[i1+]==str2[i])
        {
            i1++;
        }
        next[i]=i1;
    }
    i1=;//别忘初始化
    for(int i=;i<=len1;i++)//怎么样，是不是和求next差不多？
    {
        while(i1&&str2[i1+]!=str1[i])
        {
            i1=next[i1];
        }
        if(str2[i1+]==str1[i])
        {
            i1++;
        }
        if(i1==len2)
        {
            printf("%d\n",i-len2+);//输出str2在str1中出现的位置
            i1=next[i1];
        }
    }
    for(int i=;i<=len2;i++)
        printf("%d ",next[i]);
}

kmp到这里就结束了,接下来是哈希

哈希算法的中心思路就是用数字来表示字符串

首先我们找一个大质数，然后用H(C,K)表示字符串C中前K个字符的哈希值，以ACDA为例，得到

ACDA-->1341

H(C,1)

H(C,2)=1*b+3

H(C,3)=H(C,2)*b+4

H(C,4)=H(C,3)*b+1

看例题

上代码

#include<iostream>
#include<cstdio>
#include<cstring>
#define ull unsigned long long
using namespace std;
int l1,l2,ans,t;
ull p[],h[],s;
const long long b=;//开大 开大 开大！！！！
char s1[],s2[];
int main()
{
    scanf("%d",&t);
    p[]=;
    for(int i=;i<=;i++) p[i]=p[i-]*b;//预处理
    while(t--)
    {
        scanf("%s %s",s1+,s2+);
        l1=strlen(s1+);
        l2=strlen(s2+);
        ans=;
        s=;
        h[]=;
        for(int i=;i<=l2;i++) h[i]=h[i-]*b+(ull)(s2[i]-'A'+);
        for(int i=;i<=l1;i++) s=s*b+(ull)(s1[i]-'A'+);
        for(int i=;i<=l2-l1;i++) if(h[i+l1]-h[i]*p[l1]==s) ans++;
        printf("%d\n",ans);
    }
}

哈希表可以处理O（1）时间在数组里查找给定值，虽然map也可以

我们可以把数组里每个数模一个质数（大），然后存进哈希表里，但是这样会发生冲突，就像会有2个数同余，这时候我们可以用链表解决