HDU 5869.Different GCD Subarray Query-区间gcd+树状数组 (神奇的标记右移操作) (2016年ICPC大连网络赛)

树状数组。。。

Different GCD Subarray Query

Time Limit: 6000/3000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 1541    Accepted Submission(s): 599

Problem Description

This is a simple problem. The teacher gives Bob a list of problems about GCD (Greatest Common Divisor). After studying some of them, Bob thinks that GCD is so interesting. One day, he comes up with a new problem about GCD. Easy as it looks, Bob cannot figure it out himself. Now he turns to you for help, and here is the problem:
  
  Given an array a of N positive integers a1,a2,⋯aN−1,aN; a subarray of a is defined as a continuous interval between a1 and aN. In other words, ai,ai+1,⋯,aj−1,aj is a subarray of a, for 1≤i≤j≤N. For a query in the form (L,R), tell the number of different GCDs contributed by all subarrays of the interval [L,R].
  

 

Input

There are several tests, process till the end of input.
  
  For each test, the first line consists of two integers N and Q, denoting the length of the array and the number of queries, respectively. N positive integers are listed in the second line, followed by Q lines each containing two integers L,R for a query.

You can assume that 
  
    1≤N,Q≤100000 
    
   1≤ai≤1000000

 

Output

For each query, output the answer in one line.

 

Sample Input

5 3

1 3 4 6 9

3 5

2 5

1 5

 

Sample Output

6

6

6

 

Source

2016 ACM/ICPC Asia Regional Dalian Online

 

这个题的意思就是问区间内所有子段不同gcd的个数。

一开始理解错了题意，后来想明白了。假设区间的数为1 2 3 4

就是gcd(1),gcd(2),gcd(3),gcd(4),gcd(1,2),gcd(2,3),gcd(3,4),gcd(1,2,3),gcd(2,3,4),gcd(1,2,3,4)这些里面不同的gcd的个数是多少。

如果用在线算法操作，每查询一次就要处理依次数据，一方面会造成浪费，另一方面，你这样写妥妥的超时啊，所以要用离线算法，将所有的数据处理好之后，按顺序直接输出结果就可以。

首先用一个数组将数据保存起来，然后用一个vector数组将查询的区间和查询的顺序记录下来。

处理数据，就是相对来说固定右端点，从右往左移，在代码里就是对于每一个i(固定右端点)，遍历一下i所在的子段的gcd，因为i不变，j是上一个i的gcd的值保存的顺序，j越大，i所在的子段就依次向左增加一个数，如果gcd发生了变化，就记录一下这个gcd以及出现的位置。可能越说越乱，画一个图表示一下。。。

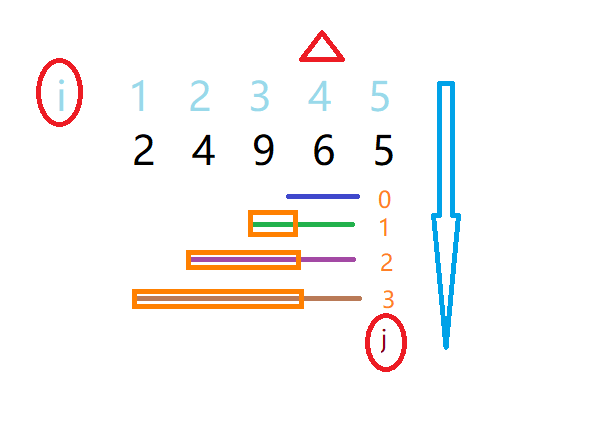
图的意思就是假设数据为2 4 9 6 5，i为下标。假设i为4，就是固定4，然后遍历j，j存的是上一个i的子段的gcd，通过上一个i的gcd来得到i为4时(6)的子段的gcd，图中画的横线的长度就是子段的长度，橙色的矩形包含的长度是上一个i处理出的数据。就是固定右端点，依次往左遍历得到所有的gcd，这样不会重复操作，也不会漏掉某个子段。

将gcd整理出来之后，怎么操作才能使得区间查询的是不同的gcd的个数呢？

对于区间内相同的gcd，让标记gcd的下标尽量右移，找该gcd的最大右端点。

通过树状数组维护gcd的下标。

一边维护，一边查询树状数组就可以保证数据正确。

总结一下就是:固定右端点，依次往左找出来所有的gcd，并标记下标，因为是i逐渐增大的，所以后面遍历的时候也是相同gcd的最大右端点。直接查询就可以。

就这样吧，不想好好写了。

代码:

 //离线处理-树状数组
 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #include<cmath>
 #include<cstdlib>
 #include<algorithm>
 #include<queue>
 #include<vector>
 #include<utility>
 using namespace std;
 const int maxn=1e5+;
 int Arr[maxn];//存数据一开始的值
 int N,Q;
 int pos[maxn*]; //记录gcd的位置
 vector<pair<int ,int> >querys[maxn];
 vector<pair<int, int> >gcds[maxn];
 int ans[maxn];
 int treeArr[maxn]; //树状数组

 int gcd(int a,int b){ //gcd求最大公约数
     if(!(a%b))return b;
     else return gcd(b,a%b);
 }

 void init(){ //初始化
     int tmp,ts;
     for(int i=;i<=N;i++){
         tmp=Arr[i];
         ts=i;                                     //固定右端点，向左遍历
         for(int j=;j<gcds[i-].size();j++){
             int tmpgcd=gcd(tmp,gcds[i-][j].first);
             if(tmpgcd!=tmp){  //如果gcd发生变化
                 gcds[i].push_back(make_pair(tmp,ts)); //first存gcd，second存gcd的左端点ts
                 ts=gcds[i-][j].second; //上一个gcd的右端点就是下一个gcd的左端点
                 tmp=tmpgcd;
             }
         }
         gcds[i].push_back(make_pair(tmp,ts)); //将与上一个的最左端的gcd存起来
     }
     return;
 }

 int lowbit(int x){  //取最低位的1
     return x&(-x);
 }

 void Add(int cur,int num){ //单点更新
     for(int i=cur;i<=N;i+=lowbit(i))
         treeArr[i]+=num;   //由叶子节点向上更新树状数组
     return;
 }

 int Query(int cur){ //区间查询  从右端点往左加二进制最低位1的
     int sum=;
     for(int i=cur;i>;i-=lowbit(i))
         sum+=treeArr[i];
     return sum;
 }

 void Solve(){
     memset(pos,,sizeof(pos));
     memset(treeArr,,sizeof(treeArr));
     for(int i=;i<=N;i++){
         for(int j=;j<gcds[i].size();j++){
             if(pos[gcds[i][j].first]){ //如果标记已经存在，就将标记去掉，所以执行单点更新操作
                 Add(pos[gcds[i][j].first],-);
             }
             Add(gcds[i][j].second,);//一个新的不同的gcd，从叶子节点开始更新个数+1
             pos[gcds[i][j].first]=gcds[i][j].second;//记录该gcd的右端点
         }
         for(int j=;j<querys[i].size();j++){
             ans[querys[i][j].second]=Query(i)-Query(querys[i][j].first-);//区间右端点-区间左区间
         }
     }
     for(int i=;i<=Q;i++)
         printf("%d\n",ans[i]);

     return;
 }
 int main(){
     //reopen("input","r",stdin);
     while(~scanf("%d%d",&N,&Q)){
         for(int i=;i<=N;i++){
             scanf("%d",&Arr[i]); //将数据存在Arr数组中
             querys[i].clear(); //清空
             gcds[i].clear(); //清空
         }
         init();
         int tmp1,tmp2;
         for(int i=;i<=Q;i++){
             scanf("%d%d",&tmp1,&tmp2);
             querys[tmp2].push_back(make_pair(tmp1,i)); //将tmp1与i成对插入vector的tmp2下标里
         }
         Solve();
     }
     return ;
 }

就这样吧，这题没什么，主要是想明白就很简单。

咸鱼太菜，学长要捶爆我的狗头吗？？？

已经做好了被学长打死的思想准备。。。