[机器视觉] SIFT特征-尺度不变特征理解

SIFT特征-尺度不变特征理解

简介

SIFT，即尺度不变特征变换（Scale-invariant feature transform，SIFT），是用于图像处理领域的一种描述。这种描述具有尺度不变性，可在图像中检测出关键点，是一种局部特征描述子。该方法于1999年由David Lowe首先发表于计算机视觉国际会议（International Conference on Computer Vision，ICCV），2004年再次经David Lowe整理完善后发表于International journal of computer vision（IJCV）。截止2014年8月，该论文单篇被引次数达25000余次。

特点

• 对旋转、尺度缩放、亮度变化保持不变性，对视角变化、噪声等也存在一定程度的稳定性
• 独特性，信息量丰富，适用于在海量特征数据中进行快速，准确的匹配
• 多量性，即使少数几个物体也可以产生大量的Sfit特征向量
• 可扩展性，可以很方便的与其他形式的特征向量进行联合

高斯图像金字塔

理解

高斯图像金字塔是把原图像先放大一倍（如150✖150到300✖300），对这个放大后的图像进行高斯滤波（之前讲过的高斯模糊，可以回去看一下），其中模糊半径分别取σ、kσ、k^2σ等等，得到若干个模糊后的图像，这是第一组，然后依次按照比例为2缩小图像，如此重复，构建一个有若干组(Octave)的金字塔，每组分为若干层。

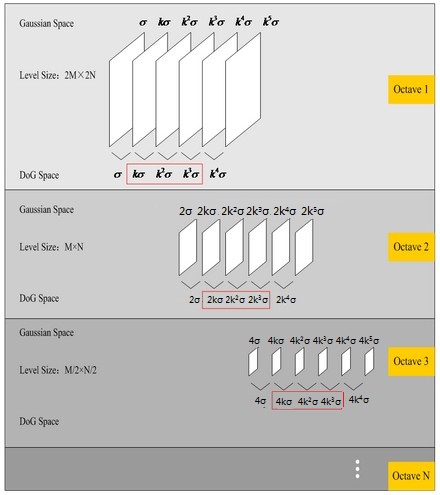
补充

用O表示octave（第几组）,用L表示layer（第几层），则（O,L）就代表高斯图像空间中的确定的一副图像。

DOG金字塔

理解

DOG金字塔（Difference of Gaussian）就是高斯金字塔同一octave下相邻两层的差分构成的金字塔。

解释

之所以要构建差分金字塔，就是为了找到在不同尺度和不同模糊程度下的不变特征，而这正式SIFT要提取的"稳定"特征。

空间极值点检测

理解

这里的空间极值点检测，其实就是在DOG空间的一个octave下比较每一个像素和它相邻点的大小，看它是否比其他点都要大。如果比周围点都大，说明它是是局部的极值点（这一点我们可以类比一个二次函数，它的最低点是不是比周围点都小，所以它是极值点，当然它也恰巧是最低点）。

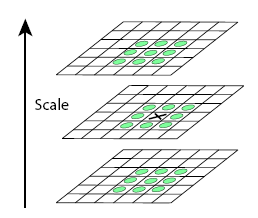
补充

这里我们要计算图中打x的点是不是极值点，那么我们就要比较它与不同层以及同层的周围一共26个点的大小，才能确定它是不是空间的极值点。

关键点精确定位

理解

由于我们上面的操作都是在离散空间操作的，我们知道，离散空间取到的极值点，并不一定是真正的极值点，所以我们需要通过类似函数拟合的方式，对离散点进行拟合使之连续，在连续空间就很容易利用我们的知识求取极值点。

计算

我们将DOG空间的泰勒展开式子看成其拟合函数，就可以操作连续空间的函数了。
候选特征点x，其偏移量定义为Δx，其对比度为D(x)的绝对值∣D(x)∣，对D(x)应用泰勒展开式

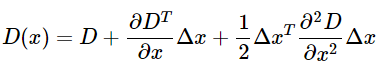
由于x是D(x)的极值点，所以对上式求导并令其为0，得到

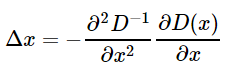
然后再把求得的Δx代入到D(x)的泰勒展开式中

设对比度的阈值为T，若∣D(x^)∣≥T，则该特征点保留，否则剔除掉。

关键方向匹配

理解

上面说了，SIFT特征具有旋转不变性，而它的旋转不变性就在于每一个关键点都有一个基准方向，而这个基准方向是由图像的局部决定和分配的。

计算

梯度的模值和方向定义如下：

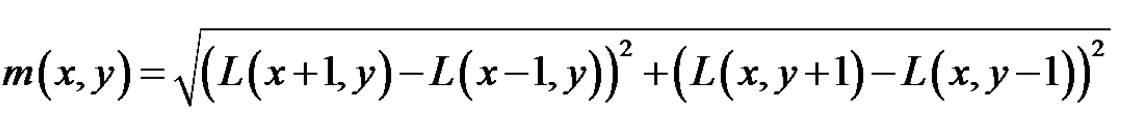
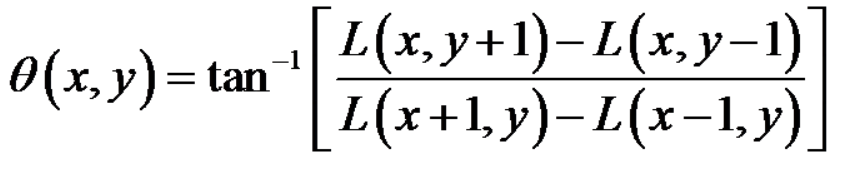
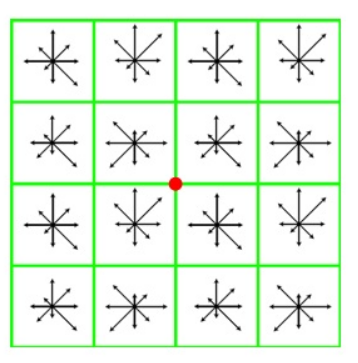
利用这个公式计算以关键点为中心的领域内所有点的梯度方向（8个方向），计算完之后，我们使用直方图来统计领域内像素的梯度和方向。梯度直方图将0~360度的方向分为36个立柱，每柱10度。直方图的峰值代表的是该关键点的主方向。为了增强鲁棒性，如果由立柱的值大于峰值的80%，我们将其作为关键点的辅方向。（下图只花了8个方向）。

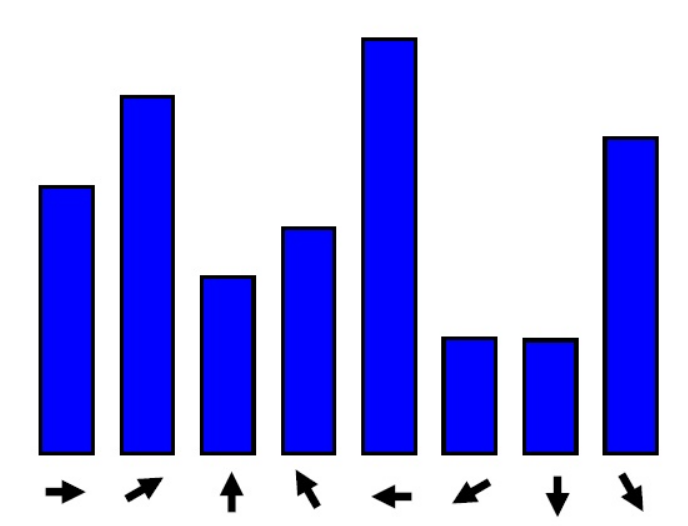
关键点描述

理解

关键点描述是对领域内高斯图像直方图统计结果的一种表示形式，我们找到的特征点参数有位置、尺度和方向。在关键点周围的领域内，将其分为m✖m个子块，每个子块以中间点为原点，分别计算梯度直方图，生成局部向量，对该向量进行标准高斯函数加权处理，然后对特征向量进行归一化处理。每个关键点在下图中可以产生2✖2✖8维向量作为特征向量。

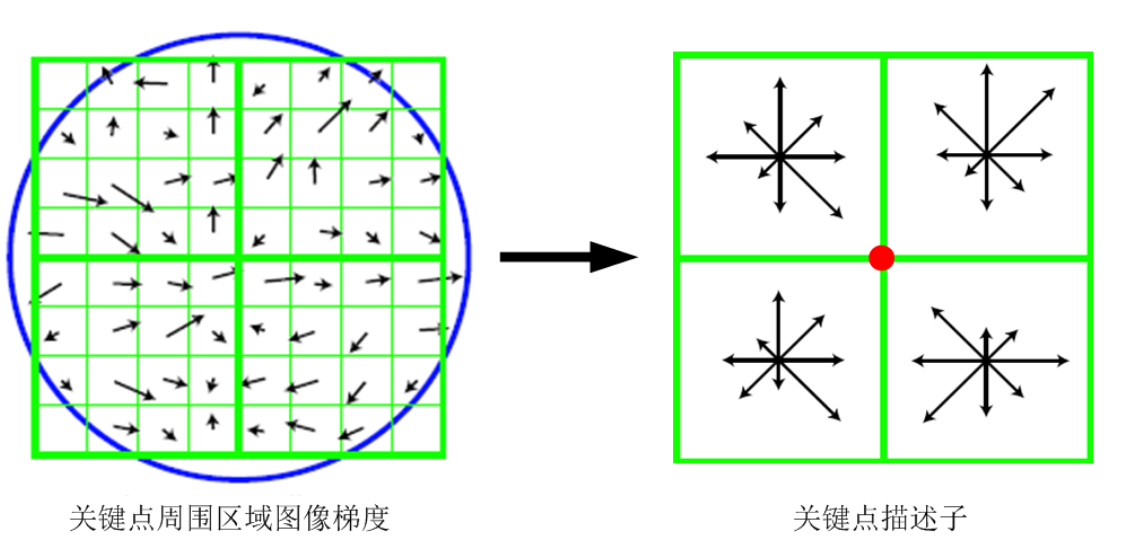
David G.Lowed的实验结果表明：对每个关键点，采用448共128维向量的描述子进项关键点表征，综合效果最佳：

特征点匹配

理解

有了目标图片，对目标图片计算SIFT特征，然后用其特征向量与已知特征的特征向量进行欧式距离匹配，其欧式距离越小，匹配度越高。