剑指Offer的学习笔记（C#篇）-- 跳台阶

题目描述

一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法（先后次序不同算不同的结果）。

一 . 解题思路。

由题目可知，青蛙一次可以跳一阶或者两阶。假设台阶为N阶，我们可以这样想：

假设青蛙最后一跳为一阶，此时预留出最后的一阶，是不是青蛙跳(N-1)阶与跳N阶，可能出现的方法一样呢（肯定一样啦，哈哈）

假设青蛙最后一跳为二阶，此时预留出最后的两阶，是不是青蛙跳(N-2)阶与跳N阶，可能出现的方法一样呢（也是一样哦，有点绕吗？）

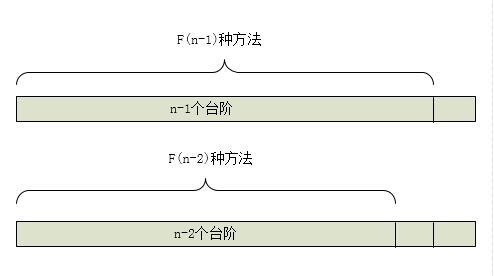
因为青蛙的极限就是一次跳2阶，所以不可能出现最后预留三阶的情况，因此，该题目其实是一个斐波那契数列的应用而已，完全可以想象成斐波那契数列来做。因此，即出现了递归与循环两种解题方法。当然，效率我们之前在斐波那契数列讨论过了，所以，此次不再继续讨论（记住循环更好就是了）。

二 . 代码实现（C#）

方法一：低效的递归法

class Solution {
    public int jumpFloor(int number){
        if(number==||number==)
       {
            return number;
        }
        else
        {
        return jumpFloor(number-)+jumpFloor(number-);
         }
    }
}

方法二：高效的循环法

class Solution
{
    public int jumpFloor(int number)
    {
        // write code here
        int x = ;
        int y = ;
        int n = ;
        if(number<)
        {
            return number;
        }
        else
        {
            for (int i = ;i<=number;i++)
            {
                n = x+y;
                x = y;
                y = n;
            }
            return n;
        }
    }
}