MATLAB——解数独

数独

数独是一种逻辑游戏，玩家需要根据9x9盘面的已知数字，推理出剩余所有空格的数字，并满足每一行、每一列和每个粗线宫(3x3)内均含1~9,不重复。

MATLAB中有关函数

M = dlmread(filename,delimiter) 使用指定的分隔符，将该文件的数据读取到矩阵M中，并将重复的分隔符视为单个的分隔符

disp(x) 显示变量x的值，而不打印变量名称

代码实现

文件目录

check3_by_3.m
check_cell.m
check_col.m
check_row.m
data.txt
shudu.m
slove.m

check3_by_3.m

 function res = check3_by_3(matrix,i,j,num)
 %检查（i,j）能否放num
     res = true;
     block_row = floor((i - ) / ) + ;
     block_col = floor((j - ) / ) + ;

     block_row_to = block_row * ;
     block_row_from = block_row_to - ;
     block_col_to = block_col * ;
     block_col_from = block_col_to - ;

     for row = block_row_from : block_row_to
         for col = block_col_from : block_col_to
             if matrix(row,col) == num
                 res = false;
                 break;
             end
         end
     end
 end

check_cell.m

 function res = check_cell(matrix,i,j,num)
 %按九宫格检查(i,j)能否放num
     if check_row(matrix,i,j,num) && check_col(matrix,i,j,num) && check3_by_3(matrix,i,j,num)
         res = true;
     else
         res = false;
     end
 end

check_col.m

 function res = check_col(matrix,i,j,num)
 %按列检查(i,j)能否放num
     res = true;
     for row =  :
         if matrix(row,j) == num
             res = false;
             break;
         end
     end
 end

check_row.m

 function res = check_row(matrix,i,j,num)
 %按行检查(i,j)能否放num
     res = true;
     for col =  :
         if matrix(i,col) == num
             res = false;
             break;
         end
     end
 end

data.txt (想要破解的数独矩阵)

5 3 0 0 7 0 0 0 0
6 0 0 1 9 5 0 0 0
0 9 8 0 0 0 0 6 0
8 0 0 0 6 0 0 0 3
4 0 0 8 0 3 0 0 1
7 0 0 0 2 0 0 0 6
0 6 0 0 0 0 2 8 0
0 0 0 4 1 9 0 0 5
0 0 0 0 8 0 0 7 9

shudu.m (主程序)

 matrix = dlmread('data3.txt','');
 disp(matrix);
 solve(matrix,);

slove.m

 function solve(matrix,id)
 %按编号逐一填充，递归
     if id >
         disp(matrix);
     else
         row = floor((id - ) / ) + ;
         col = mod((id - ),) + ;

         if matrix(row,col) ~=
             solve(matrix,id + );
         else
             for i =  :
                 if check_cell(matrix,row,col,i) == true
                 matrix(row,col) = i;
                 solve(matrix,id + );
                 end
             end
         end
    end
 end

效果图

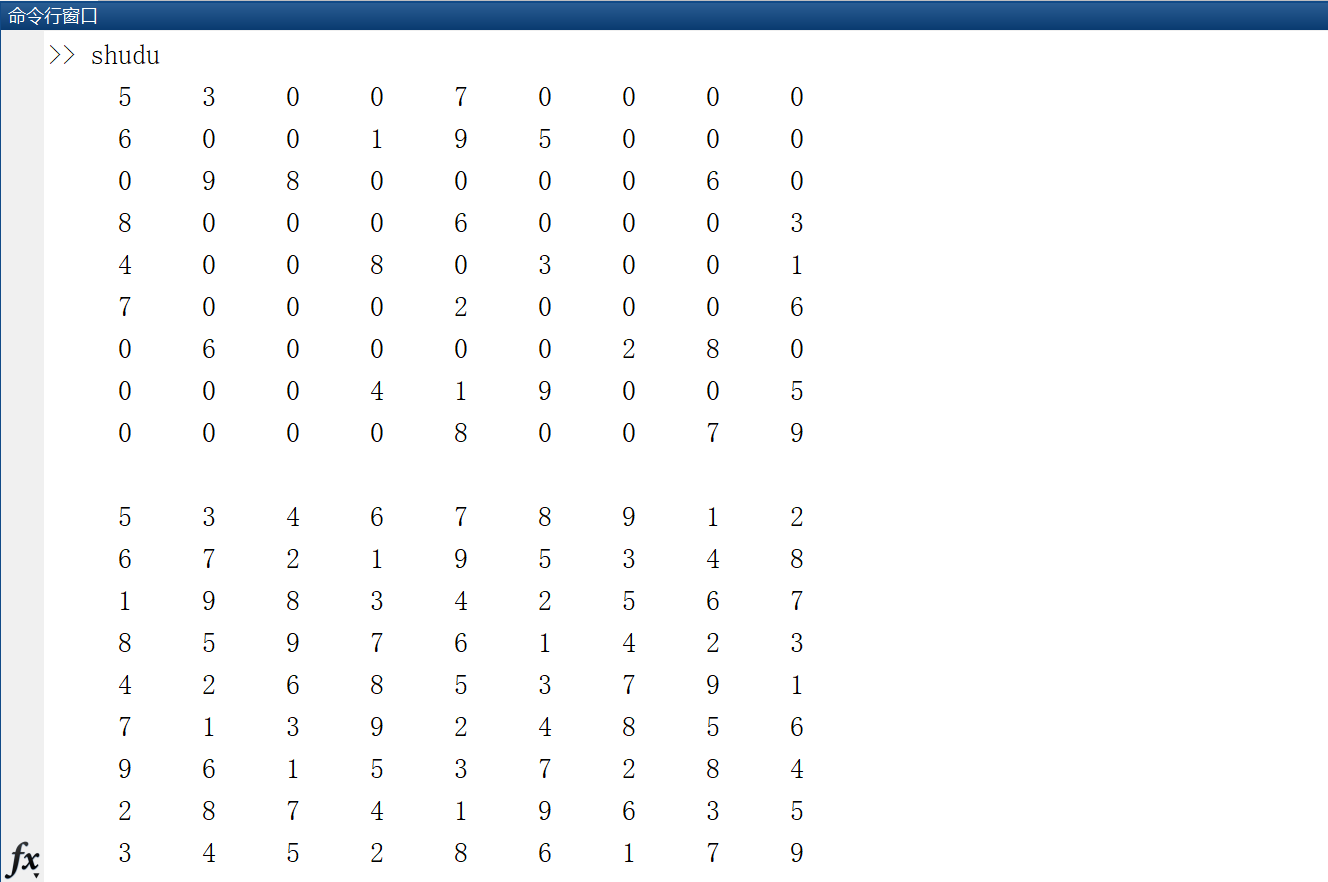
参考链接：https://youtu.be/La57P8wNnLA