UVA11419 我是SAM

题意：

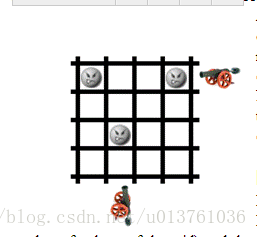
     给你一个n*m的矩阵，上面有一些格子上有目标，我们可以在格子的外面用枪打目标，一发子弹可以消灭一行或者一列目标，问你最少多少枪能把目标打光，并且输出开枪的位置，题目没说spj(特判),但显然是特判。

                    

思路：

      求最少多少枪好办，就是求最小顶点覆盖，这个大家都知道，关键是求方案，白书上当时说的是什么匈牙利树，表示没听过，没办法，愣是在网上找到一个代码不停的模拟那个所谓匈牙利树什么的过程，现在我说下我的理解：

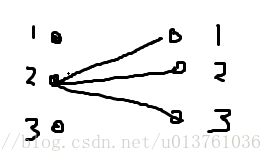
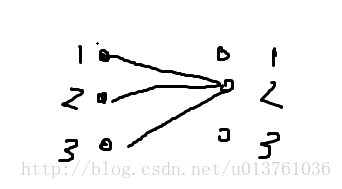
我们要处理的其实就是这样两种情况的各种组合。

（1）


这个显然是在左边2行开枪

（2）

这个显然是在右边2行开枪

那么遇到这样的一个个组合我们怎么找呢？我们可以利用匈牙利算法的性质，我们在左侧没有匹配的行让他继续匹配，匹配尝试中，凡是能设计到左边的点都mark上，mark上的点就是不用开枪的点，凡是设计到的又边的点也mark上，mark上的点都是能开枪的点，只要你了解匈牙利的过程，这个很容易理解，建议自己模拟下，迷茫的时候模拟是最快的学习方法。

具体细节看下代码吧！比较容易理解。




#include<stdio.h>

#include<string.h>

#define N_node 1000 + 10

#define N_edge 1000000 + 10

typedef struct

{

   int to ,next;

}STAR;

STAR E[N_edge];

int list[N_node] ,tot;

int mk_gxl[N_node] ,mk_gxr[N_node];

int mkl[N_node] ,mkr[N_node];

void add(int a, int b)

{

   E[++tot].to = b;

   E[tot].next = list[a];

   list[a] = tot;

}

int DFS_XYL(int x)

{

   mkl[x] = 1;

   for(int k = list[x] ;k ;k = E[k].next)

   {

      int to = E[k].to;

      if(mkr[to]) continue;

      mkr[to] = 1;

      if(mk_gxr[to] == -1 || DFS_XYL(mk_gxr[to]))

      {

         mk_gxr[to] = x;

         mk_gxl[x] =  to;

         return 1;

      }

   }

   return 0;

}

int main ()

{

   int R ,C ,i ,Ans ,n ,a ,b;

   while(~scanf("%d %d %d" ,&R ,&C ,&n) && R + C + n)

   {

      memset(list ,0 ,sizeof(list)) ,tot = 1;

      for(i = 1 ;i <= n ;i ++)

      {

         scanf("%d %d" ,&a ,&b);

         add(a ,b);

      }

      Ans = 0;

      memset(mk_gxl ,255 ,sizeof(mk_gxl));

      memset(mk_gxr ,255 ,sizeof(mk_gxr));

      for(i = 1 ;i <= R ;i ++)

      {

         memset(mkr ,0 ,sizeof(mkr));

         Ans += DFS_XYL(i);

      }

      printf("%d" ,Ans);

      

      memset(mkr ,0 ,sizeof(mkr));

      memset(mkl ,0 ,sizeof(mkl));

      for(i = 1 ;i <= R ;i ++)

      if(mk_gxl[i] == -1) DFS_XYL(i);

      for(i = 1 ;i <= R ;i ++)

      if(!mkl[i]) printf(" r%d" ,i);

      for(i = 1 ;i <= C ;i ++)

      if(mkr[i])  printf(" c%d" ,i);

      printf("\n");

   }

   return 0;

}